More on Personal Growth

Alexander Nguyen
3 years ago
How can you bargain for $300,000 at Google?
Don’t give a number

Google pays its software engineers generously. While many of their employees are competent, they disregard a critical skill to maximize their pay.
Negotiation.
If Google employees have never negotiated, they're as helpless as anyone else.
In this piece, I'll reveal a compensation negotiation tip that will set you apart.
The Fallacy of Negotiating
How do you negotiate your salary? “Just give them a number twice the amount you really want”. - Someplace on the internet
Above is typical negotiation advice. If you ask for more than you want, the recruiter may meet you halfway.
It seems logical and great, but here's why you shouldn't follow that advice.
Haitian hostage rescue
In 1977, an official's aunt was kidnapped in Haiti. The kidnappers demanded $150,000 for the aunt's life. It seems reasonable until you realize why kidnappers want $150,000.
FBI detective and negotiator Chris Voss researched why they demanded so much.
“So they could party through the weekend”
When he realized their ransom was for partying, he offered $4,751 and a CD stereo. Criminals freed the aunt.
These thieves gave 31.57x their estimated amount and got a fraction. You shouldn't trust these thieves to negotiate your compensation.
What happened?
Negotiating your offer and Haiti
This narrative teaches you how to negotiate with a large number.
You can and will be talked down.
If a recruiter asks your wage expectation and you offer double, be ready to explain why.
If you can't justify your request, you may be offered less. The recruiter will notice and talk you down.
Reasonably,
a tiny bit more than the present amount you earn
a small premium over an alternative offer
a little less than the role's allotted amount
Real-World Illustration

Recruiter: What’s your expected salary? Candidate: (I know the role is usually $100,000) $200,000 Recruiter: How much are you compensated in your current role? Candidate: $90,000 Recruiter: We’d be excited to offer you $95,000 for your experiences for the role.
So Why Do They Even Ask?
Recruiters ask for a number to negotiate a lower one. Asking yourself limits you.
You'll rarely get more than you asked for, and your request can be lowered.
The takeaway from all of this is to never give an expected compensation.
Tell them you haven't thought about it when you applied.

Rajesh Gupta
3 years ago
Why Is It So Difficult to Give Up Smoking?

I started smoking in 2002 at IIT BHU. Most of us thought it was enjoyable at first. I didn't realize the cost later.
In 2005, during my final semester, I lost my father. Suddenly, I felt more accountable for my mother and myself.
I quit before starting my first job in Bangalore. I didn't see any smoking friends in my hometown for 2 months before moving to Bangalore.
For the next 5-6 years, I had no regimen and smoked only when drinking.
Due to personal concerns, I started smoking again after my 2011 marriage. Now smoking was a constant guilty pleasure.
I smoked 3-4 cigarettes a day, but never in front of my family or on weekends. I used to excuse this with pride! First office ritual: smoking. Even with guilt, I couldn't stop this time because of personal concerns.
After 8-9 years, in mid 2019, a personal development program solved all my problems. I felt complete in myself. After this, I just needed one cigarette each day.
The hardest thing was leaving this final cigarette behind, even though I didn't want it.
James Clear's Atomic Habits was published last year. I'd only read 2-3 non-tech books before reading this one in August 2021. I knew everything but couldn't use it.
In April 2022, I realized the compounding effect of a bad habit thanks to my subconscious mind. 1 cigarette per day (excluding weekends) equals 240 = 24 packs per year, which is a lot. No matter how much I did, it felt negative.
Then I applied the 2nd principle of this book, identifying the trigger. I tried to identify all the major triggers of smoking. I found social drinking is one of them & If I am able to control it during that time, I can easily control it in other situations as well. Going further whenever I drank, I was pre-determined to ignore the craving at any cost. Believe me, it was very hard initially but gradually this craving started fading away even with drinks.
I've been smoke-free for 3 months. Now I know a bad habit's effects. After realizing the power of habits, I'm developing other good habits which I ignored all my life.

Darius Foroux
2 years ago
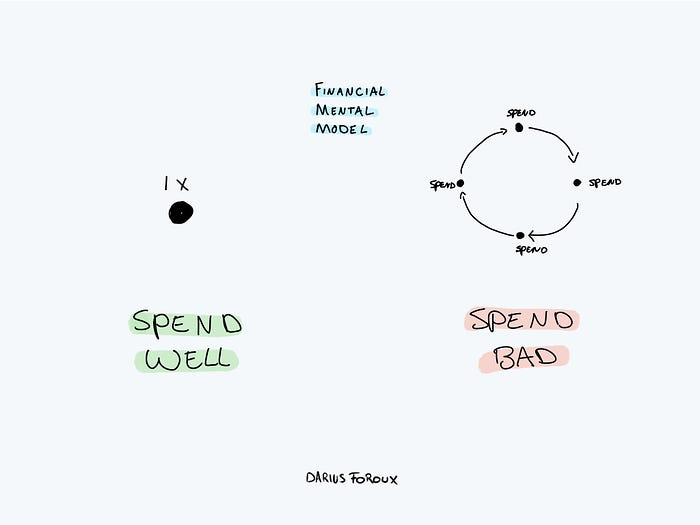
My financial life was changed by a single, straightforward mental model.
Prioritize big-ticket purchases
I've made several spending blunders. I get sick thinking about how much money I spent.
My financial mental model was poor back then.
Stoicism and mindfulness keep me from attaching to those feelings. It still hurts.
Until four or five years ago, I bought a new winter jacket every year.
Ten years ago, I spent twice as much. Now that I have a fantastic, warm winter parka, I don't even consider acquiring another one. No more spending. I'm not looking for jackets either.
Saving time and money by spending well is my thinking paradigm.
The philosophy is expressed in most languages. Cheap is expensive in the Netherlands. This applies beyond shopping.
In this essay, I will offer three examples of how this mental paradigm transformed my financial life.
Publishing books
In 2015, I presented and positioned my first book poorly.
I called the book Huge Life Success and made a funny Canva cover in 30 minutes. This:

That looks nothing like my present books. No logo or style. The book felt amateurish.
The book started bothering me a few weeks after publication. The advice was good, but it didn't appear professional. I studied the book business extensively.
I created a style for all my designs. Branding. Win Your Inner Wars was reissued a year later.
Title, cover, and description changed. Rearranging the chapters improved readability.
Seven years later, the book sells hundreds of copies a month. That taught me a lot.
Rushing to finish a project is enticing. Send it and move forward.
Avoid rushing everything. Relax. Develop your projects. Perform well. Perform the job well.
My first novel was underfunded and underworked. A bad book arrived. I then invested time and money in writing the greatest book I could.
That book still sells.
Traveling
I hate travel. Airports, flights, trains, and lines irritate me.
But, I enjoy traveling to beautiful areas.
I do it strangely. I make up travel rules. I never go to airports in summer. I hate being near airports on holidays. Unworthy.
No vacation packages for me. Those airline packages with a flight, shuttle, and hotel. I've had enough.
I try to avoid crowds and popular spots. July Paris? Nuts and bolts, please. Christmas in NYC? No, please keep me sane.
I fly business class behind. I accept upgrades upon check-in. I prefer driving. I drove from the Netherlands to southern Spain.
Thankfully, no lines. What if travel costs more? Thus? I enjoy it from the start. I start traveling then.
I rarely travel since I'm so difficult. One great excursion beats several average ones.
Personal effectiveness
New apps, tools, and strategies intrigue most productivity professionals.
No.
I researched years ago. I spent years investigating productivity in university.
I bought books, courses, applications, and tools. It was expensive and time-consuming.
Im finished. Productivity no longer costs me time or money. OK. I worked on it once and now follow my strategy.
I avoid new programs and systems. My stuff works. Why change winners?
Spending wisely saves time and money.
Spending wisely means spending once. Many people ignore productivity. It's understudied. No classes.
Some assume reading a few articles or a book is enough. Productivity is personal. You need a personal system.
Time invested is one-time. You can trust your system for life once you find it.
Concentrate on the expensive choices.
Life's short. Saving money quickly is enticing.
Spend less on groceries today. True. That won't fix your finances.
Adopt a lifestyle that makes you affluent over time. Consider major choices.
Are they causing long-term poverty? Are you richer?
Leasing cars comes to mind. The automobile costs a fortune today. The premium could accomplish a million nice things.
Focusing on important decisions makes life easier. Consider your future. You want to improve next year.
You might also like

David G Chen
3 years ago
If you want to earn money, stop writing for entertainment.
When you stop blogging for a few weeks, your views and profits plummet.
Because you're writing fascinating posts for others. Everyone's done ithat…
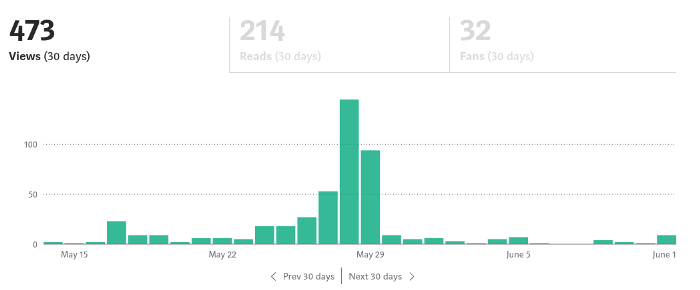
If I keep writing, the graph should maintain velocity, you could say. If I wrote more, it could rise.
However, entertaining pieces still tend to roller coaster and jump.
this type of writing is like a candle. They burn out and must be replaced. You must continuously light new ones to maintain the illumination.
When you quit writing, your income stops.
A substitute
Instead of producing amusing articles, try solving people's issues. You should answer their search questions.
Here's what happens when you answer their searches.
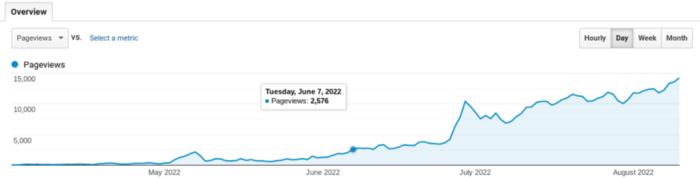
My website's Google analytics. As a dentist, I answer oral health questions.
This chart vs. Medium is pretty glaring, right?
As of yesterday, it was averaging 15k page views each day.
How much would you make on Medium with 15k daily views?
Evergreen materials
In SEO, this is called evergreen content.
Your content is like a lush, evergreen forest, and by green I mean Benjamins.

Do you have knowledge that you can leverage? Why not help your neighbors and the world?
Answer search inquiries and help others. You'll be well rewarded.
This is better than crafting candle-like content that fizzles out quickly.
Is beauty really ephemeral like how flowers bloom? Nah, I prefer watching forests grow instead (:

CoinTelegraph
4 years ago
2 NFT-based blockchain games that could soar in 2022
NFTs look ready to rule 2022, and the recent pivot toward NFT utility in P2E gaming could make blockchain gaming this year’s sector darling.
After the popularity of decentralized finance (DeFi) came the rise of nonfungible tokens (NFTs), and to the surprise of many, NFTs took the spotlight and now remain front and center with the highest volume in sales occurring at the start of January 2022.
While 2021 became the year of NFTs, GameFi applications did surpass DeFi in terms of user popularity. According to data from DappRadar, Bloomberg gathered:
Nearly 50% of active cryptocurrency wallets connected to decentralized applications in November were for playing games. The percentage of wallets linked to decentralized finance, or DeFi, dapps fell to 45% during the same period, after months of being the leading dapp use case.
Blockchain play-to-earn (P2E) game Axie infinity skyrocketed and kicked off a gaming craze that is expected to continue all throughout 2022. Crypto pundits and gaming advocates have high expectations for P2E blockchain-based games and there’s bound to be a few sleeping giants that will dominate the sector.
Let’s take a look at five blockchain games that could make waves in 2022.
DeFi Kingdoms
The inspiration for DeFi Kingdoms came from simple beginnings — a passion for investing that lured the developers to blockchain technology. DeFi Kingdoms was born as a visualization of liquidity pool investing where in-game ‘gardens’ represent literal and figurative token pairings and liquidity pool mining.
As shown in the game, investors have a portion of their LP share within a plot filled with blooming plants. By attaching the concept of growth to DeFi protocols within a play-and-earn model, DeFi Kingdoms puts a twist on “playing” a game.
Built on the Harmony Network, DeFi Kingdoms became the first project on the network to ever top the DappRadar charts. This could be attributed to an influx of individuals interested in both DeFi and blockchain games or it could be attributed to its recent in-game utility token JEWEL surging.
JEWEL is a utility token that allows users to purchase NFTs in-game buffs to increase a base-level stat. It is also used for liquidity mining to grant users the opportunity to make more JEWEL through staking.
JEWEL is also a governance token that gives holders a vote in the growth and evolution of the project. In the past four months, the token price surged from $1.23 to an all-time high of $22.52. At the time of writing, JEWEL is down by nearly 16%, trading at $19.51.
Surging approximately 1,487% from its humble start of $1.23 four months ago in September, JEWEL token price has increased roughly 165% this last month alone, according to data from CoinGecko.
Guild of Guardians
Guild of Guardians is one of the more anticipated blockchain games in 2022 and it is built on ImmutableX, the first layer-two solution built on Ethereum that focuses on NFTs. Aiming to provide more access, it will operate as a free-to-play mobile role-playing game, modeling the P2E mechanics.
Similar to blockchain games like Axie Infinity, Guild of Guardians in-game assets can be exchanged. The project seems to be of interest to many gamers and investors with its NFT founder sale and token launch generating nearly $10 million in volume.
Launching its in-game token in October of 2021, the Guild of Guardians (GOG) tokens are ERC-20 tokens known as ‘gems’ inside the game. Gems are what power key features in the game such as minting in-game NFTs and interacting with the marketplace, and are available to earn while playing.
For the last month, the Guild of Guardians token has performed rather steadily after spiking to its all-time high of $2.81 after its launch. Despite the token being down over 50% from its all-time high, at the time of writing, some members of the community are looking forward to the possibility of staking and liquidity pools, which are features that tend to help stabilize token prices.
Marcus Lu
3 years ago
The Brand Structure of U.S. Electric Vehicle Production
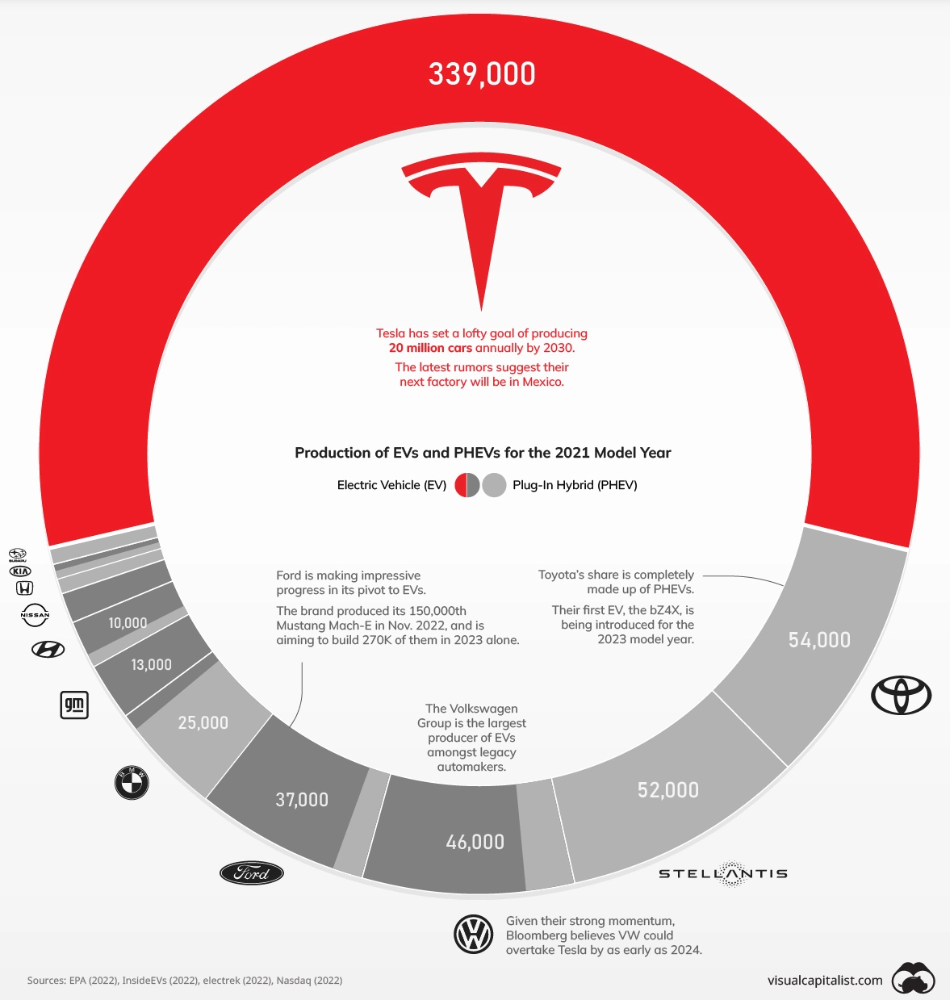
Will Tesla be able to maintain its lead in the EV market for very long?
This is one of the most pressing issues in the American auto sector today. One positive aspect of Tesla is the company's devoted customer base and recognizable name recognition (similar to Apple). It also invests more in research and development per vehicle than its rivals and has a head start in EV production.
Conversely, established automakers like Volkswagen are actively plotting their strategy to surpass Tesla. As the current market leaders, they have decades of experience in the auto industry and are spending billions to catch up.
We've visualized data from the EPA's 2022 Automotive Trends Report to bring you up to speed on this developing story.
Info for the Model Year of 2021
The full production data used in this infographic is for the 2021 model year, but it comes from a report for 2022.
Combined EV and PHEV output is shown in the table below (plug-in hybrid electric vehicle).
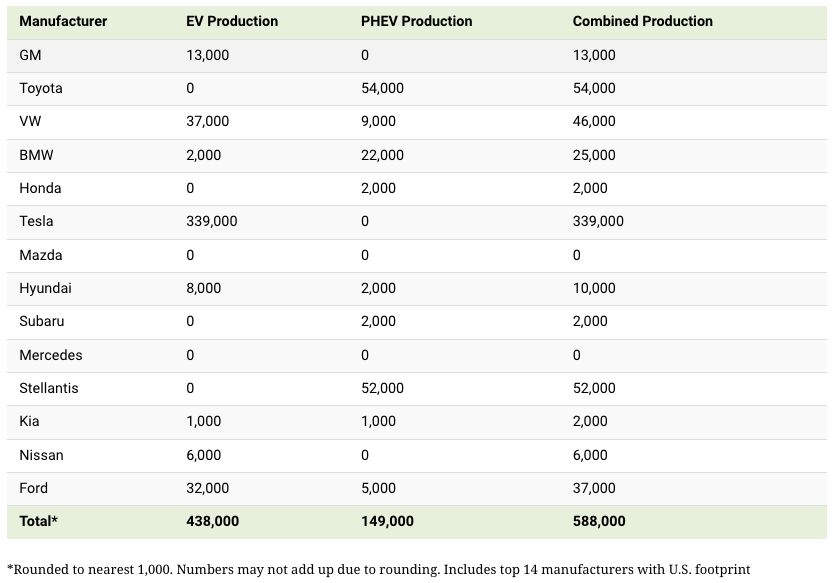
It is important to note that Toyota and Stellantis, the two largest legacy automakers in this dataset, only produced PHEVs. Toyota's first electric vehicle, the bZ4X, won't hit the market until 2023.
Stellantis seems to be falling even further behind, despite having enormous unrealized potential in its Jeep and Ram brands. Stellantis CEO Carlos Tavares said in a recent interview that the firm has budgeted $36 billion for electrification and software.
Legacy Brands with the Most Momentum
In the race to develop electric vehicles, some long-standing manufacturers have gotten the jump on their rivals.
Volkswagen, one of these storied manufacturers, has made a significant investment in electric vehicles (EVs) in the wake of the Dieselgate scandal. The company plans to roll out multiple EV models, including the ID.3 hatchback, ID.4 SUV, and ID. Buzz, with the goal of producing 22 million EVs by 2028. (an electric revival of the classic Microbus).
Even Ford is keeping up, having just announced an EV investment of $22 billion between 2021 and 2025. In November of 2022, the company manufactured their 150,000th Mustang Mach-E, and by the end of 2023, they hoped to have 270,000 of them in circulation.
Additionally, over 200,000 F-150 Lightnings have been reserved since Ford announced the truck. The Lightning is scheduled to have a production run of 15,000 in 2022, 55,000 in 2023, and 80,000 in 2024. Ford's main competitor in the electric pickup truck segment, Rivian, is on track to sell 25,000 vehicles by 2022.
