More on Web3 & Crypto

Jayden Levitt
3 years ago
The country of El Salvador's Bitcoin-obsessed president lost $61.6 million.
It’s only a loss if you sell, right?

Nayib Bukele proclaimed himself “the world’s coolest dictator”.
His jokes aren't clear.
El Salvador's 43rd president self-proclaimed “CEO of El Salvador” couldn't be less presidential.
His thin jeans, aviator sunglasses, and baseball caps like a cartel lord.
He's popular, though.
Bukele won 53% of the vote by fighting violent crime and opposition party corruption.
El Salvador's 6.4 million inhabitants are riding the cryptocurrency volatility wave.
They were powerless.
Their autocratic leader, a former Yamaha Motors salesperson and Bitcoin believer, wants to help 70% unbanked locals.
He intended to give the citizens a way to save money and cut the country's $200 million remittance cost.
Transfer and deposit costs.
This makes logical sense when the president’s theatrics don’t blind you.
El Salvador's Bukele revealed plans to make bitcoin legal tender.
Remittances total $5.9 billion (23%) of the country's expenses.
Anything that reduces costs could boost the economy.
The country’s unbanked population is staggering. Here’s the data by % of people who either have a bank account (Blue) or a mobile money account (Black).
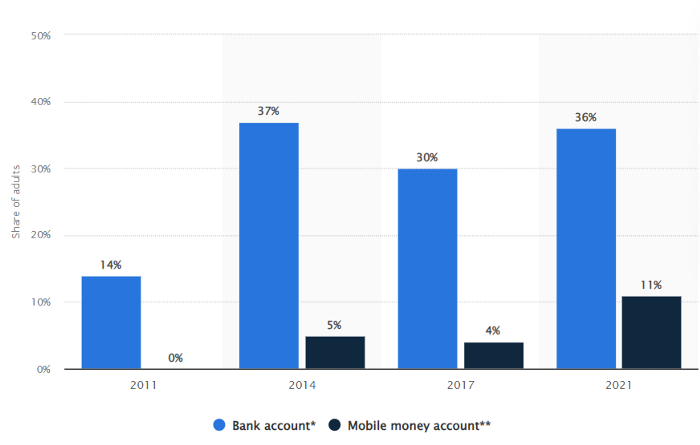
According to Bukele, 46% of the population has downloaded the Chivo Bitcoin Wallet.
In 2021, 36% of El Salvadorans had bank accounts.
Large rural countries like Kenya seem to have resolved their unbanked dilemma.
An economy surfaced where village locals would sell, trade and store network minutes and data as a store of value.
Kenyan phone networks realized unbanked people needed a safe way to accumulate wealth and have an emergency fund.
96% of Kenyans utilize M-PESA, which doesn't require a bank account.
The software involves human agents who hang out with cash and a phone.
These people are like ATMs.
You offer them cash to deposit money in your mobile money account or withdraw cash.
In a country with a faulty banking system, cash availability and a safe place to deposit it are important.
William Jack and Tavneet Suri found that M-PESA brought 194,000 Kenyan households out of poverty by making transactions cheaper and creating a safe store of value.
Mobile money, a service that allows monetary value to be stored on a mobile phone and sent to other users via text messages, has been adopted by most Kenyan households. We estimate that access to the Kenyan mobile money system M-PESA increased per capita consumption levels and lifted 194,000 households, or 2% of Kenyan households, out of poverty.
The impacts, which are more pronounced for female-headed households, appear to be driven by changes in financial behaviour — in particular, increased financial resilience and saving. Mobile money has therefore increased the efficiency of the allocation of consumption over time while allowing a more efficient allocation of labour, resulting in a meaningful reduction of poverty in Kenya.
Currently, El Salvador has 2,301 Bitcoin.
At publication, it's worth $44 million. That remains 41% of Bukele's original $105.6 million.
Unknown if the country has sold Bitcoin, but Bukeles keeps purchasing the dip.
It's still falling.

This might be a fantastic move for the impoverished country over the next five years, if they can live economically till Bitcoin's price recovers.
The evidence demonstrates that a store of value pulls individuals out of poverty, but others say Bitcoin is premature.
You may regard it as an aggressive endeavor to front run the next wave of adoption, offering El Salvador a financial upside.

Faisal Khan
2 years ago
4 typical methods of crypto market manipulation

Market fraud
Due to its decentralized and fragmented character, the crypto market has integrity difficulties.
Cryptocurrencies are an immature sector, therefore market manipulation becomes a bigger issue. Many research have attempted to uncover these abuses. CryptoCompare's newest one highlights some of the industry's most typical scams.
Why are these concerns so common in the crypto market? First, even the largest centralized exchanges remain unregulated due to industry immaturity. A low-liquidity market segment makes an attack more harmful. Finally, market surveillance solutions not implemented reduce transparency.
In CryptoCompare's latest exchange benchmark, 62.4% of assessed exchanges had a market surveillance system, although only 18.1% utilised an external solution. To address market integrity, this measure must improve dramatically. Before discussing the report's malpractices, note that this is not a full list of attacks and hacks.
Clean Trading
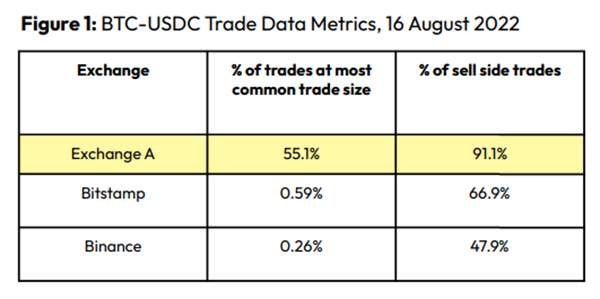
An investor buys and sells concurrently to increase the asset's price. Centralized and decentralized exchanges show this misconduct. 23 exchanges have a volume-volatility correlation < 0.1 during the previous 100 days, according to CryptoCompares. In August 2022, Exchange A reported $2.5 trillion in artificial and/or erroneous volume, up from $33.8 billion the month before.
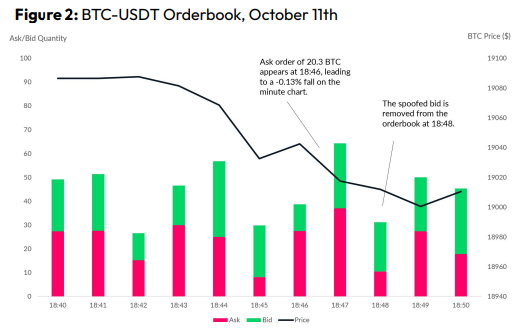
Spoofing
Criminals create and cancel fake orders before they can be filled. Since manipulators can hide in larger trading volumes, larger exchanges have more spoofing. A trader placed a 20.8 BTC ask order at $19,036 when BTC was trading at $19,043. BTC declined 0.13% to $19,018 in a minute. At 18:48, the trader canceled the ask order without filling it.
Front-Running
Most cryptocurrency front-running involves inside trading. Traditional stock markets forbid this. Since most digital asset information is public, this is harder. Retailers could utilize bots to front-run.
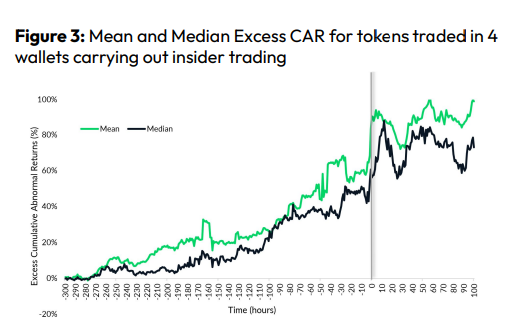
CryptoCompare found digital wallets of people who traded like insiders on exchange listings. The figure below shows excess cumulative anomalous returns (CAR) before a coin listing on an exchange.
Finally, LAYERING is a sequence of spoofs in which successive orders are put along a ladder of greater (layering offers) or lower (layering bids) values. The paper concludes with recommendations to mitigate market manipulation. Exchange data transparency, market surveillance, and regulatory oversight could reduce manipulative tactics.

Elnaz Sarraf
3 years ago
Why Bitcoin's Crash Could Be Good for Investors

The crypto market crashed in June 2022. Bitcoin and other cryptocurrencies hit their lowest prices in over a year, causing market panic. Some believe this crash will benefit future investors.
Before I discuss how this crash might help investors, let's examine why it happened. Inflation in the U.S. reached a 30-year high in 2022 after Russia invaded Ukraine. In response, the U.S. Federal Reserve raised interest rates by 0.5%, the most in almost 20 years. This hurts cryptocurrencies like Bitcoin. Higher interest rates make people less likely to invest in volatile assets like crypto, so many investors sold quickly.
The crypto market collapsed. Bitcoin, Ethereum, and Binance dropped 40%. Other cryptos crashed so hard they were delisted from almost every exchange. Bitcoin peaked in April 2022 at $41,000, but after the May interest rate hike, it crashed to $28,000. Bitcoin investors were worried. Even in bad times, this crash is unprecedented.
Bitcoin wasn't "doomed." Before the crash, LUNA was one of the top 5 cryptos by market cap. LUNA was trading around $80 at the start of May 2022, but after the rate hike?
Less than 1 cent. LUNA lost 99.99% of its value in days and was removed from every crypto exchange. Bitcoin's "crash" isn't as devastating when compared to LUNA.
Many people said Bitcoin is "due" for a LUNA-like crash and that the only reason it hasn't crashed is because it's bigger. Still false. If so, Bitcoin should be worth zero by now. We didn't. Instead, Bitcoin reached 28,000, then 29k, 30k, and 31k before falling to 18k. That's not the world's greatest recovery, but it shows Bitcoin's safety.
Bitcoin isn't falling constantly. It fell because of the initial shock of interest rates, but not further. Now, Bitcoin's value is more likely to rise than fall. Bitcoin's low price also attracts investors. They know what prices Bitcoin can reach with enough hype, and they want to capitalize on low prices before it's too late.

Bitcoin's crash was bad, but in a way it wasn't. To understand, consider 2021. In March 2021, Bitcoin surpassed $60k for the first time. Elon Musk's announcement in May that he would no longer support Bitcoin caused a massive crash in the crypto market. In May 2017, Bitcoin's price hit $29,000. Elon Musk's statement isn't worth more than the Fed raising rates. Many expected this big announcement to kill Bitcoin.

Not so. Bitcoin crashed from $58k to $31k in 2021. Bitcoin fell from $41k to $28k in 2022. This crash is smaller. Bitcoin's price held up despite tensions and stress, proving investors still believe in it. What happened after the initial crash in the past?
Bitcoin fell until mid-July. This is also something we’re not seeing today. After a week, Bitcoin began to improve daily. Bitcoin's price rose after mid-July. Bitcoin's price fluctuated throughout the rest of 2021, but it topped $67k in November. Despite no major changes, the peak occurred after the crash. Elon Musk seemed uninterested in crypto and wasn't likely to change his mind soon. What triggered this peak? Nothing, really. What really happened is that people got over the initial statement. They forgot.
Internet users have goldfish-like attention spans. People quickly forgot the crash's cause and were back investing in crypto months later. Despite the market's setbacks, more crypto investors emerged by the end of 2017. Who gained from these peaks? Bitcoin investors who bought low. Bitcoin not only recovered but also doubled its ROI. It was like a movie, and it shows us what to expect from Bitcoin in the coming months.
The current Bitcoin crash isn't as bad as the last one. LUNA is causing market panic. LUNA and Bitcoin are different cryptocurrencies. LUNA crashed because Terra wasn’t able to keep its peg with the USD. Bitcoin is unanchored. It's one of the most decentralized investments available. LUNA's distrust affected crypto prices, including Bitcoin, but it won't last forever.
This is why Bitcoin will likely rebound in the coming months. In 2022, people will get over the rise in interest rates and the crash of LUNA, just as they did with Elon Musk's crypto stance in 2021. When the world moves on to the next big controversy, Bitcoin's price will soar.
Bitcoin may recover for another reason. Like controversy, interest rates fluctuate. The Russian invasion caused this inflation. World markets will stabilize, prices will fall, and interest rates will drop.
Next, lower interest rates could boost Bitcoin's price. Eventually, it will happen. The U.S. economy can't sustain such high interest rates. Investors will put every last dollar into Bitcoin if interest rates fall again.
Bitcoin has proven to be a stable investment. This boosts its investment reputation. Even if Ethereum dethrones Bitcoin as crypto king one day (or any other crypto, for that matter). Bitcoin may stay on top of the crypto ladder for a while. We'll have to wait a few months to see if any of this is true.
This post is a summary. Read the full article here.
You might also like
Matthew Royse
3 years ago
These 10 phrases are unprofessional at work.
Successful workers don't talk this way.

"I know it's unprofessional, but I can't stop." — Author Sandy Hall
Do you realize your unprofessionalism? Do you care? Self-awareness?
Everyone can improve their unprofessionalism. Some workplace phrases and words shouldn't be said.
People often say out loud what they're thinking. They show insecurity, incompetence, and disrespect.
"Think before you speak," goes the saying.
Some of these phrases are "okay" in certain situations, but you'll lose colleagues' respect if you use them often.
Your word choice. Your tone. Your intentions. They matter.
Choose your words carefully to build work relationships and earn peer respect. You should build positive relationships with coworkers and clients.
These 10 phrases are unprofessional.
1. That Meeting Really Sucked
Wow! Were you there? You should be responsible if you attended. You can influence every conversation.
Alternatives
Improve the meeting instead of complaining afterward. Make it more meaningful and productive.
2. Not Sure if You Saw My Last Email
Referencing a previous email irritates people. Email follow-up can be difficult. Most people get tons of emails a day, so it may have been buried, forgotten, or low priority.
Alternatives
It's okay to follow up, but be direct, short, and let the recipient "save face"
3. Any Phrase About Sex, Politics, and Religion
Discussing sex, politics, and religion at work is foolish. If you discuss these topics, you could face harassment lawsuits.
Alternatives
Keep quiet about these contentious issues. Don't touch them.
4. I Know What I’m Talking About
Adding this won't persuade others. Research, facts, and topic mastery are key to persuasion. If you're knowledgeable, you don't need to say this.
Alternatives
Please don’t say it at all. Justify your knowledge.
5. Per Our Conversation
This phrase sounds like legal language. You seem to be documenting something legally. Cold, stern, and distant. "As discussed" sounds inauthentic.
Alternatives
It was great talking with you earlier; here's what I said.
6. Curse-Word Phrases
Swearing at work is unprofessional. You never know who's listening, so be careful. A child may be at work or on a Zoom or Teams call. Workplace cursing is unacceptable.
Alternatives
Avoid adult-only words.
7. I Hope This Email Finds You Well
This is a unique way to wish someone well. This phrase isn't as sincere as the traditional one. When you talk about the email, you're impersonal.
Alternatives
Genuinely care for others.
8. I Am Really Stressed
Happy, strong, stress-managing coworkers are valued. Manage your own stress. Exercise, sleep, and eat better.
Alternatives
Everyone has stress, so manage it. Don't talk about your stress.
9. I Have Too Much to Do
You seem incompetent. People think you can't say "no" or have poor time management. If you use this phrase, you're telling others you may need to change careers.
Alternatives
Don't complain about your workload; just manage it.
10. Bad Closing Salutations
"Warmly," "best," "regards," and "warm wishes" are common email closings. This conclusion sounds impersonal. Why use "warmly" for finance's payment status?
Alternatives
Personalize the closing greeting to the message and recipient. Use "see you tomorrow" or "talk soon" as closings.
Bringing It All Together
These 10 phrases are unprofessional at work. That meeting sucked, not sure if you saw my last email, and sex, politics, and religion phrases.
Also, "I know what I'm talking about" and any curse words. Also, avoid phrases like I hope this email finds you well, I'm stressed, and I have too much to do.
Successful workers communicate positively and foster professionalism. Don't waste chances to build strong work relationships by being unprofessional.
“Unprofessionalism damages the business reputation and tarnishes the trust of society.” — Pearl Zhu, an American author
This post is a summary. Read full article here

Dr. Linda Dahl
3 years ago
We eat corn in almost everything. Is It Important?

Corn Kid got viral on TikTok after being interviewed by Recess Therapy. Tariq, called the Corn Kid, ate a buttery ear of corn in the video. He's corn crazy. He thinks everyone just has to try it. It turns out, whether we know it or not, we already have.
Corn is a fruit, veggie, and grain. It's the second-most-grown crop. Corn makes up 36% of U.S. exports. In the U.S., it's easy to grow and provides high yields, as proven by the vast corn belt spanning the Midwest, Great Plains, and Texas panhandle. Since 1950, the corn crop has doubled to 10 billion bushels.
You say, "Fine." We shouldn't just grow because we can. Why so much corn? What's this corn for?
Why is practical and political. Michael Pollan's The Omnivore's Dilemma has the full narrative. Early 1970s food costs increased. Nixon subsidized maize to feed the public. Monsanto genetically engineered corn seeds to make them hardier, and soon there was plenty of corn. Everyone ate. Woot! Too much corn followed. The powers-that-be had to decide what to do with leftover corn-on-the-cob.
They are fortunate that corn has a wide range of uses.
First, the edible variants. I divide corn into obvious and stealth.
Obvious corn includes popcorn, canned corn, and corn on the cob. This form isn't always digested and often comes out as entire, polka-dotting poop. Cornmeal can be ground to make cornbread, polenta, and corn tortillas. Corn provides antioxidants, minerals, and vitamins in moderation. Most synthetic Vitamin C comes from GMO maize.
Corn oil, corn starch, dextrose (a sugar), and high-fructose corn syrup are often overlooked. They're stealth corn because they sneak into practically everything. Corn oil is used for frying, baking, and in potato chips, mayonnaise, margarine, and salad dressing. Baby food, bread, cakes, antibiotics, canned vegetables, beverages, and even dairy and animal products include corn starch. Dextrose appears in almost all prepared foods, excluding those with high-fructose corn syrup. HFCS isn't as easily digested as sucrose (from cane sugar). It can also cause other ailments, which we'll discuss later.
Most foods contain corn. It's fed to almost all food animals. 96% of U.S. animal feed is corn. 39% of U.S. corn is fed to livestock. But animals prefer other foods. Omnivore chickens prefer insects, worms, grains, and grasses. Captive cows are fed a total mixed ration, which contains corn. These animals' products, like eggs and milk, are also corn-fed.
There are numerous non-edible by-products of corn that are employed in the production of items like:
fuel-grade ethanol
plastics
batteries
cosmetics
meds/vitamins binder
carpets, fabrics
glutathione
crayons
Paint/glue

How does corn influence you? Consider quick food for dinner. You order a cheeseburger, fries, and big Coke at the counter (or drive-through in the suburbs). You tell yourself, "No corn." All that contains corn. Deconstruct:
Cows fed corn produce meat and cheese. Meat and cheese were bonded with corn syrup and starch (same). The bun (corn flour and dextrose) and fries were fried in maize oil. High fructose corn syrup sweetens the drink and helps make the cup and straw.
Just about everything contains corn. Then what? A cornspiracy, perhaps? Is eating too much maize an issue, or should we strive to stay away from it whenever possible?
As I've said, eating some maize can be healthy. 92% of U.S. corn is genetically modified, according to the Center for Food Safety. The adjustments are expected to boost corn yields. Some sweet corn is genetically modified to produce its own insecticide, a protein deadly to insects made by Bacillus thuringiensis. It's safe to eat in sweet corn. Concerns exist about feeding agricultural animals so much maize, modified or not.
High fructose corn syrup should be consumed in moderation. Fructose, a sugar, isn't easily metabolized. Fructose causes diabetes, fatty liver, obesity, and heart disease. It causes inflammation, which might aggravate gout. Candy, packaged sweets, soda, fast food, juice drinks, ice cream, ice cream topping syrups, sauces & condiments, jams, bread, crackers, and pancake syrup contain the most high fructose corn syrup. Everyday foods with little nutrients. Check labels and choose cane sugar or sucrose-sweetened goods. Or, eat corn like the Corn Kid.

Alison Randel
3 years ago
Raising the Bar on Your 1:1s

Managers spend much time in 1:1s. Most team members meet with supervisors regularly. 1:1s can help create relationships and tackle tough topics. Few appreciate the 1:1 format's potential. Most of the time, that potential is spent on small talk, surface-level updates, and ranting (Ugh, the marketing team isn’t stepping up the way I want them to).
What if you used that time to have deeper conversations and important insights? What if change was easy?
This post introduces a new 1:1 format to help you dive deeper, faster, and develop genuine relationships without losing impact.
A 1:1 is a chat, you would assume. Why use structure to talk to a coworker? Go! I know how to talk to people. I can write. I've always written. Also, This article was edited by Zoe.
Before you discard something, ask yourself if there's a good reason not to try anything new. Is the 1:1 only a talk, or do you want extra benefits? Try the steps below to discover more.
I. Reflection (5 minutes)
Context-free, broad comments waste time and are useless. Instead, give team members 5 minutes to write these 3 prompts.
What's effective?
What is decent but could be improved?
What is broken or missing?
Why these? They encourage people to be honest about all their experiences. Answering these questions helps people realize something isn't working. These prompts let people consider what's working.
Why take notes? Because you get more in less time. Will you feel awkward sitting quietly while your coworker writes? Probably. Persevere. Multi-task. Take a break from your afternoon meeting marathon. Any awkwardness will pay off.
What happens? After a few minutes of light conversation, create a template like the one given here and have team members fill in their replies. You can pre-share the template (with the caveat that this isn’t meant to take much prep time). Do this with your coworker: Answer the prompts. Everyone can benefit from pondering and obtaining guidance.
This step's output.

Part II: Talk (10-20 minutes)
Most individuals can explain what they see but not what's behind an answer. You don't like a meeting. Why not? Marketing partnership is difficult. What makes working with them difficult? I don't recommend slandering coworkers. Consider how your meetings, decisions, and priorities make work harder. The excellent stuff too. You want to know what's humming so you can reproduce the magic.
First, recognize some facts.
Real power dynamics exist. To encourage individuals to be honest, you must provide a safe environment and extend clear invites. Even then, it may take a few 1:1s for someone to feel secure enough to go there in person. It is part of your responsibility to admit that it is normal.
Curiosity and self-disclosure are crucial. Most leaders have received training to present themselves as the authorities. However, you will both benefit more from the dialogue if you can be open and honest about your personal experience, ask questions out of real curiosity, and acknowledge the pertinent sacrifices you're making as a leader.
Honesty without bias is difficult and important. Due to concern for the feelings of others, people frequently hold back. Or if they do point anything out, they do so in a critical manner. The key is to be open and unapologetic about what you observe while not presuming that your viewpoint is correct and that of the other person is incorrect.
Let's go into some prompts (based on genuine conversations):
“What do you notice across your answers?”
“What about the way you/we/they do X, Y, or Z is working well?”
“ Will you say more about item X in ‘What’s not working?’”
“I’m surprised there isn’t anything about Z. Why is that?”
“All of us tend to play some role in maintaining certain patterns. How might you/we be playing a role in this pattern persisting?”
“How might the way we meet, make decisions, or collaborate play a role in what’s currently happening?”
Consider the preceding example. What about the Monday meeting isn't working? Why? or What about the way we work with marketing makes collaboration harder? Remember to share your honest observations!
Third section: observe patterns (10-15 minutes)
Leaders desire to empower their people but don't know how. We also have many preconceptions about what empowerment means to us and how it works. The next phase in this 1:1 format will assist you and your team member comprehend team power and empowerment. This understanding can help you support and shift your team member's behavior, especially where you disagree.
How to? After discussing the stated responses, ask each team member what they can control, influence, and not control. Mark their replies. You can do the same, adding colors where you disagree.
This step's output.

Next, consider the color constellation. Discuss these questions:
Is one color much more prevalent than the other? Why, if so?
Are the colors for the "what's working," "what's fine," and "what's not working" categories clearly distinct? Why, if so?
Do you have any disagreements? If yes, specifically where does your viewpoint differ? What activities do you object to? (Remember, there is no right or wrong in this. Give explicit details and ask questions with curiosity.)
Example: Based on the colors, you can ask, Is the marketing meeting's quality beyond your control? Were our marketing partners consulted? Are there any parts of team decisions we can control? We can't control people, but have we explored another decision-making method? How can we collaborate and generate governance-related information to reduce work, even if the requirement for prep can't be eliminated?
Consider the top one or two topics for this conversation. No 1:1 can cover everything, and that's OK. Focus on the present.
Part IV: Determine the next step (5 minutes)
Last, examine what this conversation means for you and your team member. It's easy to think we know the next moves when we don't.
Like what? You and your teammate answer these questions.
What does this signify moving ahead for me? What can I do to change this? Make requests, for instance, and see how people respond before thinking they won't be responsive.
What demands do I have on other people or my partners? What should I do first? E.g. Make a suggestion to marketing that we hold a monthly retrospective so we can address problems and exchange input more frequently. Include it on the meeting's agenda for next Monday.
Close the 1:1 by sharing what you noticed about the chat. Observations? Learn anything?
Yourself, you, and the 1:1
As a leader, you either reinforce or disrupt habits. Try this template if you desire greater ownership, empowerment, or creativity. Consider how you affect surrounding dynamics. How can you expect others to try something new in high-stakes scenarios, like meetings with cross-functional partners or senior stakeholders, if you won't? How can you expect deep thought and relationship if you don't encourage it in 1:1s? What pattern could this new format disrupt or reinforce?
Fight reluctance. First attempts won't be ideal, and that's OK. You'll only learn by trying.
