More on Personal Growth

Merve Yılmaz
3 years ago
Dopamine detox
This post is for you if you can't read or study for 5 minutes.

If you clicked this post, you may be experiencing problems focusing on tasks. A few minutes of reading may tire you. Easily distracted? Using social media and video games for hours without being sidetracked may impair your dopamine system.
When we achieve a goal, the brain secretes dopamine. It might be as simple as drinking water or as crucial as college admission. Situations vary. Various events require different amounts.
Dopamine is released when we start learning but declines over time. Social media algorithms provide new material continually, making us happy. Social media use slows down the system. We can't continue without an award. We return to social media and dopamine rewards.
Mice were given a button that released dopamine into their brains to study the hormone. The mice lost their hunger, thirst, and libido and kept pressing the button. Think this is like someone who spends all day gaming or on Instagram?
When we cause our brain to release so much dopamine, the brain tries to balance it in 2 ways:
1- Decreases dopamine production
2- Dopamine cannot reach its target.
Too many quick joys aren't enough. We'll want more joys. Drugs and alcohol are similar. Initially, a beer will get you drunk. After a while, 3-4 beers will get you drunk.
Social media is continually changing. Updates to these platforms keep us interested. When social media conditions us, we can't read a book.
Same here. I used to complete a book in a day and work longer without distraction. Now I'm addicted to Instagram. Daily, I spend 2 hours on social media. This must change. My life needs improvement. So I started the 50-day challenge.
I've compiled three dopamine-related methods.
Recommendations:
Day-long dopamine detox
First, take a day off from all your favorite things. Social media, gaming, music, junk food, fast food, smoking, alcohol, friends. Take a break.
Hanging out with friends or listening to music may seem pointless. Our minds are polluted. One day away from our pleasures can refresh us.
2. One-week dopamine detox by selecting
Choose one or more things to avoid. Social media, gaming, music, junk food, fast food, smoking, alcohol, friends. Try a week without Instagram or Twitter. I use this occasionally.
One week all together
One solid detox week. It's the hardest program. First or second options are best for dopamine detox. Time will help you.
You can walk, read, or pray during a dopamine detox. Many options exist. If you want to succeed, you must avoid instant gratification. Success after hard work is priceless.

Katrine Tjoelsen
3 years ago
8 Communication Hacks I Use as a Young Employee
Learn these subtle cues to gain influence.

Hate being ignored?
As a 24-year-old, I struggled at work. Attention-getting tips How to avoid being judged by my size, gender, and lack of wrinkles or gray hair?
I've learned seniority hacks. Influence. Within two years as a product manager, I led a team. I'm a Stanford MBA student.
These communication hacks can make you look senior and influential.
1. Slowly speak
We speak quickly because we're afraid of being interrupted.
When I doubt my ideas, I speak quickly. How can we slow down? Jamie Chapman says speaking slowly saps our energy.
Chapman suggests emphasizing certain words and pausing.
2. Interrupted? Stop the stopper
Someone interrupt your speech?
Don't wait. "May I finish?" No pause needed. Stop interrupting. I first tried this in Leadership Laboratory at Stanford. How quickly I gained influence amazed me.
Next time, try “May I finish?” If that’s not enough, try these other tips from Wendy R.S. O’Connor.
3. Context
Others don't always see what's obvious to you.
Through explanation, you help others see the big picture. If a senior knows it, you help them see where your work fits.
4. Don't ask questions in statements
“Your statement lost its effect when you ended it on a high pitch,” a group member told me. Upspeak, it’s called. I do it when I feel uncertain.
Upspeak loses influence and credibility. Unneeded. When unsure, we can say "I think." We can even ask a proper question.
Someone else's boasting is no reason to be dismissive. As leaders and colleagues, we should listen to our colleagues even if they use this speech pattern.
Give your words impact.
5. Signpost structure
Signposts improve clarity by providing structure and transitions.
Communication coach Alexander Lyon explains how to use "first," "second," and "third" He explains classic and summary transitions to help the listener switch topics.
Signs clarify. Clarity matters.

6. Eliminate email fluff
“Fine. When will the report be ready? — Jeff.”
Notice how senior leaders write short, direct emails? I often use formalities like "dear," "hope you're well," and "kind regards"
Formality is (usually) unnecessary.
7. Replace exclamation marks with periods
See how junior an exclamation-filled email looks:
Hi, all!
Hope you’re as excited as I am for tomorrow! We’re celebrating our accomplishments with cake! Join us tomorrow at 2 pm!
See you soon!
Why the exclamation points? Why not just one?
Hi, all.
Hope you’re as excited as I am for tomorrow. We’re celebrating our accomplishments with cake. Join us tomorrow at 2 pm!
See you soon.
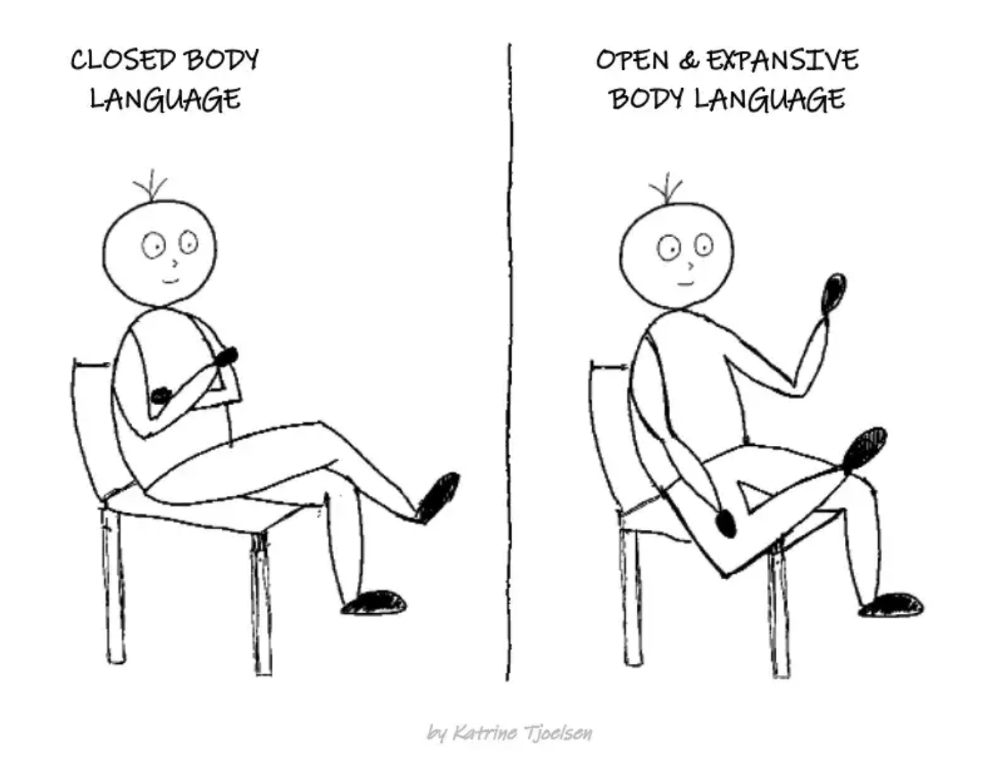
8. Take space
"Playing high" means having an open, relaxed body, says Stanford professor and author Deborah Gruenfield.
Crossed legs or looking small? Relax. Get bigger.

Theo Seeds
3 years ago
The nine novels that have fundamentally altered the way I view the world
I read 53 novels last year and hope to do so again.
Books are best if you love learning. You get a range of perspectives, unlike podcasts and YouTube channels where you get the same ones.
Book quality varies. I've read useless books. Most books teach me something.

These 9 novels have changed my outlook in recent years. They've made me rethink what I believed or introduced me to a fresh perspective that changed my worldview.
You can order these books yourself. Or, read my summaries to learn what I've synthesized.
Enjoy!
Fooled By Randomness

Nassim Taleb worked as a Wall Street analyst. He used options trading to bet on unlikely events like stock market crashes.
Using financial models, investors predict stock prices. The models assume constant, predictable company growth.
These models base their assumptions on historical data, so they assume the future will be like the past.
Fooled By Randomness argues that the future won't be like the past. We often see impossible market crashes like 2008's housing market collapse. The world changes too quickly to use historical data: by the time we understand how it works, it's changed.
Most people don't live to see history unfold. We think our childhood world will last forever. That goes double for stable societies like the U.S., which hasn't seen major turbulence in anyone's lifetime.
Fooled By Randomness taught me to expect the unexpected. The world is deceptive and rarely works as we expect. You can't always trust your past successes or what you've learned.
Antifragile

More Taleb. Some things, like the restaurant industry and the human body, improve under conditions of volatility and turbulence.
We didn't have a word for this counterintuitive concept until Taleb wrote Antifragile. The human body (which responds to some stressors, like exercise, by getting stronger) and the restaurant industry both benefit long-term from disorder (when economic turbulence happens, bad restaurants go out of business, improving the industry as a whole).
Many human systems are designed to minimize short-term variance because humans don't understand it. By eliminating short-term variation, we increase the likelihood of a major disaster.
Once, we put out every forest fire we found. Then, dead wood piled up in forests, causing catastrophic fires.
We don't like price changes, so politicians prop up markets with stimulus packages and printing money. This leads to a bigger crash later. Two years ago, we printed a ton of money for stimulus checks, and now we have double-digit inflation.
Antifragile taught me how important Plan B is. A system with one or two major weaknesses will fail. Make large systems redundant, foolproof, and change-responsive.
Reality is broken

We dread work. Work is tedious. Right?
Wrong. Work gives many people purpose. People are happiest when working. (That's why some are workaholics.)
Factory work saps your soul, office work is boring, and working for a large company you don't believe in and that operates unethically isn't satisfying.
Jane McGonigal says in Reality Is Broken that meaningful work makes us happy. People love games because they simulate good work. McGonigal says work should be more fun.
Some think they'd be happy on a private island sipping cocktails all day. That's not true. Without anything to do, most people would be bored. Unemployed people are miserable. Many retirees die within 2 years, much more than expected.
Instead of complaining, find meaningful work. If you don't like your job, it's because you're in the wrong environment. Find the right setting.
The Lean Startup

Before the airplane was invented, Harvard scientists researched flying machines. Who knew two North Carolina weirdos would beat them?
The Wright Brothers' plane design was key. Harvard researchers were mostly theoretical, designing an airplane on paper and trying to make it fly in theory. They'd build it, test it, and it wouldn't fly.
The Wright Brothers were different. They'd build a cheap plane, test it, and it'd crash. Then they'd learn from their mistakes, build another plane, and it'd crash.
They repeated this until they fixed all the problems and one of their planes stayed aloft.
Mistakes are considered bad. On the African savannah, one mistake meant death. Even today, if you make a costly mistake at work, you'll be fired as a scapegoat. Most people avoid failing.
In reality, making mistakes is the best way to learn.
Eric Reis offers an unintuitive recipe in The Lean Startup: come up with a hypothesis, test it, and fail. Then, try again with a new hypothesis. Keep trying, learning from each failure.
This is a great startup strategy. Startups are new businesses. Startups face uncertainty. Run lots of low-cost experiments to fail, learn, and succeed.
Don't fear failing. Low-cost failure is good because you learn more from it than you lose. As long as your worst-case scenario is acceptable, risk-taking is good.
The Sovereign Individual

Today, nation-states rule the world. The UN recognizes 195 countries, and they claim almost all land outside of Antarctica.
We agree. For the past 2,000 years, much of the world's territory was ungoverned.
Why today? Because technology has created incentives for nation-states for most of the past 500 years. The logic of violence favors nation-states, according to James Dale Davidson, author of the Sovereign Individual. Governments have a lot to gain by conquering as much territory as possible, so they do.
Not always. During the Dark Ages, Europe was fragmented and had few central governments. Partly because of armor. With armor, a sword, and a horse, you couldn't be stopped. Large states were hard to form because they rely on the threat of violence.
When gunpowder became popular in Europe, violence changed. In a world with guns, assembling large armies and conquest are cheaper.
James Dale Davidson says the internet will make nation-states obsolete. Most of the world's wealth will be online and in people's heads, making capital mobile.
Nation-states rely on predatory taxation of the rich to fund large militaries and welfare programs.
When capital is mobile, people can live anywhere in the world, Davidson says, making predatory taxation impossible. They're not bound by their job, land, or factory location. Wherever they're treated best.
Davidson says that over the next century, nation-states will collapse because they won't have enough money to operate as they do now. He imagines a world of small city-states, like Italy before 1900. (or Singapore today).
We've already seen some movement toward a more Sovereign Individual-like world. The pandemic proved large-scale remote work is possible, freeing workers from their location. Many cities and countries offer remote workers incentives to relocate.
Many Western businesspeople live in tax havens, and more people are renouncing their US citizenship due to high taxes. Increasing globalization has led to poor economic conditions and resentment among average people in the West, which is why politicians like Trump and Sanders rose to popularity with angry rhetoric, even though Obama rose to popularity with a more hopeful message.
The Sovereign Individual convinced me that the future will be different than Nassim Taleb's. Large countries like the U.S. will likely lose influence in the coming decades, while Portugal, Singapore, and Turkey will rise. If the trend toward less freedom continues, people may flee the West en masse.
So a traditional life of college, a big firm job, hard work, and corporate advancement may not be wise. Young people should learn as much as possible and develop flexible skills to adapt to the future.
Sapiens

Sapiens is a history of humanity, from proto-humans in Ethiopia to our internet society today, with some future speculation.
Sapiens views humans (and Homo sapiens) as a unique species on Earth. We were animals 100,000 years ago. We're slowly becoming gods, able to affect the climate, travel to every corner of the Earth (and the Moon), build weapons that can kill us all, and wipe out thousands of species.
Sapiens examines what makes Homo sapiens unique. Humans can believe in myths like religion, money, and human-made entities like countries and LLCs.
These myths facilitate large-scale cooperation. Ants from the same colony can cooperate. Any two humans can trade, though. Even if they're not genetically related, large groups can bond over religion and nationality.
Combine that with intelligence, and you have a species capable of amazing feats.
Sapiens may make your head explode because it looks at the world without presupposing values, unlike most books. It questions things that aren't usually questioned and says provocative things.
It also shows how human history works. It may help you understand and predict the world. Maybe.
The 4-hour Workweek

Things can be done better.
Tradition, laziness, bad bosses, or incentive structures cause complacency. If you're willing to make changes and not settle for the status quo, you can do whatever you do better and achieve more in less time.
The Four-Hour Work Week advocates this. Tim Ferriss explains how he made more sales in 2 hours than his 8-hour-a-day colleagues.
By firing 2 of his most annoying customers and empowering his customer service reps to make more decisions, he was able to leave his business and travel to Europe.
Ferriss shows how to escape your 9-to-5, outsource your life, develop a business that feeds you with little time, and go on mini-retirement adventures abroad.
Don't accept the status quo. Instead, level up. Find a way to improve your results. And try new things.
Why Nations Fail

Nogales, Arizona and Mexico were once one town. The US/Mexico border was arbitrarily drawn.
Both towns have similar cultures and populations. Nogales, Arizona is well-developed and has a high standard of living. Nogales, Mexico is underdeveloped and has a low standard of living. Whoa!
Why Nations Fail explains how government-created institutions affect country development. Strong property rights, capitalism, and non-corrupt governments promote development. Countries without capitalism, strong property rights, or corrupt governments don't develop.
Successful countries must also embrace creative destruction. They must offer ordinary citizens a way to improve their lot by creating value for others, not reducing them to slaves, serfs, or peasants. Authors say that ordinary people could get rich on trading expeditions in 11th-century Venice.
East and West Germany and North and South Korea have different economies because their citizens are motivated differently. It explains why Chile, China, and Singapore grow so quickly after becoming market economies.
People have spent a lot of money on third-world poverty. According to Why Nations Fail, education and infrastructure aren't the answer. Developing nations must adopt free-market economic policies.
Elon Musk

Elon Musk is the world's richest man, but that’s not a good way to describe him. Elon Musk is the world's richest man, which is like calling Steve Jobs a turtleneck-wearer or Benjamin Franklin a printer.
Elon Musk does cool sci-fi stuff to help humanity avoid existential threats.
Oil will run out. We've delayed this by developing better extraction methods. We only have so much nonrenewable oil.
Our society is doomed if it depends on oil. Elon Musk invested heavily in Tesla and SolarCity to speed the shift to renewable energy.
Musk worries about AI: we'll build machines smarter than us. We won't be able to stop these machines if something goes wrong, just like cows can't fight humans. Neuralink: we need to be smarter to compete with AI when the time comes.
If Earth becomes uninhabitable, we need a backup plan. Asteroid or nuclear war could strike Earth at any moment. We may not have much time to react if it happens in a few days. We must build a new civilization while times are good and resources are plentiful.
Short-term problems dominate our politics, but long-term issues are more important. Long-term problems can cause mass casualties and homelessness. Musk demonstrates how to think long-term.
The main reason people are impressed by Elon Musk, and why Ashlee Vances' biography influenced me so much, is that he does impossible things.
Electric cars were once considered unprofitable, but Tesla has made them mainstream. SpaceX is the world's largest private space company.
People lack imagination and dismiss ununderstood ideas as impossible. Humanity is about pushing limits. Don't worry if your dreams seem impossible. Try it.
Thanks for reading.
You might also like

William Anderson
3 years ago
When My Remote Leadership Skills Took Off
4 Ways To Manage Remote Teams & Employees
The wheels hit the ground as I landed in Rochester.
Our six-person satellite office was now part of my team.
Their manager only reported to me the day before, but I had my ticket booked ahead of time.
I had managed remote employees before but this was different. Engineers dialed into headquarters for every meeting.
So when I learned about the org chart change, I knew a strong first impression would set the tone for everything else.
I was either their boss, or their boss's boss, and I needed them to know I was committed.
Managing a fleet of satellite freelancers or multiple offices requires treating others as more than just a face behind a screen.
You must comprehend each remote team member's perspective and daily interactions.
The good news is that you can start using these techniques right now to better understand and elevate virtual team members.
1. Make Visits To Other Offices
If budgeted, visit and work from offices where teams and employees report to you. Only by living alongside them can one truly comprehend their problems with communication and other aspects of modern life.
2. Have Others Come to You
• Having remote, distributed, or satellite employees and teams visit headquarters every quarter or semi-quarterly allows the main office culture to rub off on them.
When remote team members visit, more people get to meet them, which builds empathy.
If you can't afford to fly everyone, at least bring remote managers or leaders. Hopefully they can resurrect some culture.
3. Weekly Work From Home
No home office policy?
Make one.
WFH is a team-building, problem-solving, and office-viewing opportunity.
For dial-in meetings, I started working from home on occasion.
It also taught me which teams “forget” or “skip” calls.
As a remote team member, you experience all the issues first hand.
This isn't as accurate for understanding teams in other offices, but it can be done at any time.
4. Increase Contact Even If It’s Just To Chat
Don't underestimate office banter.
Sometimes it's about bonding and trust, other times it's about business.
If you get all this information in real-time, please forward it.
Even if nothing critical is happening, call remote team members to check in and chat.
I guarantee that building relationships and rapport will increase both their job satisfaction and yours.

Francesca Furchtgott
3 years ago
Giving customers what they want or betraying the values of the brand?
A J.Crew collaboration for fashion label Eveliina Vintage is not a paradox; it is a solution.

Eveliina Vintage's capsule collection debuted yesterday at J.Crew. This J.Crew partnership stopped me in my tracks.
Eveliina Vintage sells vintage goods. Eeva Musacchia founded the shop in Finland in the 1970s. It's recognized for its one-of-a-kind slip dresses from the 1930s and 1940s.
I wondered why a vintage brand would partner with a mass shop. Fast fashion against vintage shopping? Will Eveliina Vintages customers be turned off?
But Eveliina Vintages customers don't care about sustainability. They want Eveliina's Instagram look. Eveliina Vintage collaborated with J.Crew to give customers what they wanted: more Eveliina at a lower price.
Vintage: A Fashion Option That Is Eco-Conscious
Secondhand shopping is a trendy response to quick fashion. J.Crew releases hundreds of styles annually. Waste and environmental damage have been criticized. A pair of jeans requires 1,800 gallons of water. J.Crew's limited-time deals promote more purchases. J.Crew items are likely among those Americans wear 7 times before discarding.
Consumers and designers have emphasized sustainability in recent years. Stella McCartney and Eileen Fisher are popular eco-friendly brands. They've also flocked to ThredUp and similar sites.
Gap, Levis, and Allbirds have listened to consumer requests. They promote recycling, ethical sourcing, and secondhand shopping.
Secondhand shoppers feel good about reusing and recycling clothing that might have ended up in a landfill.
Eco-conscious fashionistas shop vintage. These shoppers enjoy the thrill of the hunt (that limited-edition Chanel bag!) and showing off a unique piece (nobody will have my look!). They also reduce their environmental impact.
Is Eveliina Vintage capitalizing on an aesthetic or is it a sustainable brand?
Eveliina Vintage emphasizes environmental responsibility. Vogue's Amanda Musacchia emphasized sustainability. Amanda, founder Eeva's daughter, is a company leader.
But Eveliina's press message doesn't address sustainability, unlike Instagram. Scarcity and fame rule.
Eveliina Vintages Instagram has see-through dresses and lace-trimmed slip dresses. Celebrities and influencers are often photographed in Eveliina's apparel, which has 53,000+ followers. Vogue appreciates Eveliina's style. Multiple publications discuss Alexa Chung's Eveliina dress.
Eveliina Vintage markets its one-of-a-kind goods. It teases future content, encouraging visitors to return. Scarcity drives demand and raises clothing prices. One dress is $1,600+, but most are $500-$1,000.
The catch: Eveliina can't monetize its expanding popularity due to exorbitant prices and limited quantity. Why?
Most people struggle to pay for their clothing. But Eveliina Vintage lacks those more affordable entry-level products, in contrast to other luxury labels that sell accessories or perfume.
Many people have trouble fitting into their clothing. The bodies of most women in the past were different from those for which vintage clothing was designed. Each Eveliina dress's specific measurements are mentioned alongside it. Be careful, you can fall in love with an ill-fitting dress.
No matter how many people can afford it and fit into it, there is only one item to sell. To get the item before someone else does, those people must be on the Eveliina Vintage website as soon as it becomes available.
A Way for Eveliina Vintage to Make Money (and Expand) with J.Crew Its following
Eveliina Vintages' cooperation with J.Crew makes commercial sense.
This partnership spreads Eveliina's style. Slightly better pricing The $390 outfits have multicolored slips and gauzy cotton gowns. Sizes range from 00 to 24, which is wider than vintage racks.
Eveliina Vintage customers like the combination. Excited comments flood the brand's Instagram launch post. Nobody is mocking the 50-year-old vintage brand's fast-fashion partnership.
Vintage may be a sustainable fashion trend, but that's not why Eveliina's clients love the brand. They only care about the old look.
And that is a tale as old as fashion.

Matthew Cluff
3 years ago
GTO Poker 101
"GTO" (Game Theory Optimal) has been used a lot in poker recently. To clarify its meaning and application, the aim of this article is to define what it is, when to use it when playing, what strategies to apply for how to play GTO poker, for beginner and more advanced players!
Poker GTO
In poker, you can choose between two main winning strategies:
Exploitative play maximizes expected value (EV) by countering opponents' sub-optimal plays and weaker tendencies. Yes, playing this way opens you up to being exploited, but the weaker opponents you're targeting won't change their game to counteract this, allowing you to reap maximum profits over the long run.
GTO (Game-Theory Optimal): You try to play perfect poker, which forces your opponents to make mistakes (which is where almost all of your profit will be derived from). It mixes bluffs or semi-bluffs with value bets, clarifies bet sizes, and more.
GTO vs. Exploitative: Which is Better in Poker?
Before diving into GTO poker strategy, it's important to know which of these two play styles is more profitable for beginners and advanced players. The simple answer is probably both, but usually more exploitable.
Most players don't play GTO poker and can be exploited in their gameplay and strategy, allowing for more profits to be made using an exploitative approach. In fact, it’s only in some of the largest games at the highest stakes that GTO concepts are fully utilized and seen in practice, and even then, exploitative plays are still sometimes used.
Knowing, understanding, and applying GTO poker basics will create a solid foundation for your poker game. It's also important to understand GTO so you can deviate from it to maximize profits.
GTO Poker Strategy
According to Ed Miller's book "Poker's 1%," the most fundamental concept that only elite poker players understand is frequency, which could be in relation to cbets, bluffs, folds, calls, raises, etc.
GTO poker solvers (downloadable online software) give solutions for how to play optimally in any given spot and often recommend using mixed strategies based on select frequencies.
In a river situation, a solver may tell you to call 70% of the time and fold 30%. It may also suggest calling 50% of the time, folding 35% of the time, and raising 15% of the time (with a certain range of hands).
Frequencies are a fundamental and often unrecognized part of poker, but they run through these 5 GTO concepts.
1. Preflop ranges
To compensate for positional disadvantage, out-of-position players must open tighter hand ranges.
Premium starting hands aren't enough, though. Considering GTO poker ranges and principles, you want a good, balanced starting hand range from each position with at least some hands that can make a strong poker hand regardless of the flop texture (low, mid, high, disconnected, etc).
Below is a GTO preflop beginner poker chart for online 6-max play, showing which hand ranges one should open-raise with. Table positions are color-coded (see key below).
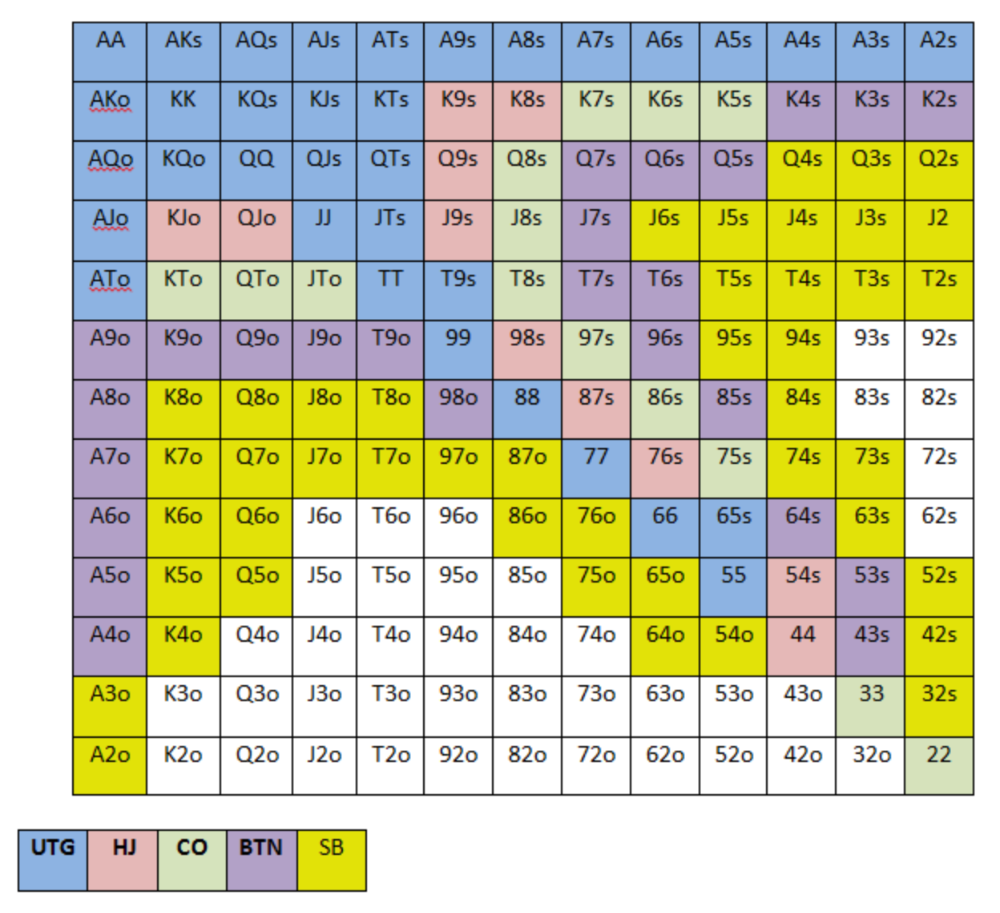
NOTE: For GTO play, it's advisable to use a mixed strategy for opening in the small blind, combining open-limps and open-raises for various hands. This cannot be illustrated with the color system used for the chart.
Choosing which hands to play is often a math problem, as discussed below.
Other preflop GTO poker charts include which hands to play after a raise, which to 3bet, etc. Solvers can help you decide which preflop hands to play (call, raise, re-raise, etc.).
2. Pot Odds
Always make +EV decisions that profit you as a poker player. Understanding pot odds (and equity) can help.
Postflop Pot Odds
Let’s say that we have JhTh on a board of 9h8h2s4c (open-ended straight-flush draw). We have $40 left and $50 in the pot. He has you covered and goes all-in. As calling or folding are our only options, playing GTO involves calculating whether a call is +EV or –EV. (The hand was empty.)
Any remaining heart, Queen, or 7 wins the hand. This means we can improve 15 of 46 unknown cards, or 32.6% of the time.
What if our opponent has a set? The 4h or 2h could give us a flush, but it could also give the villain a boat. If we reduce outs from 15 to 14.5, our equity would be 31.5%.
We must now calculate pot odds.
(bet/(our bet+pot)) = pot odds
= $50 / ($40 + $90)
= $40 / $130
= 30.7%
To make a profitable call, we need at least 30.7% equity. This is a profitable call as we have 31.5% equity (even if villain has a set). Yes, we will lose most of the time, but we will make a small profit in the long run, making a call correct.
Pot odds aren't just for draws, either. If an opponent bets 50% pot, you get 3 to 1 odds on a call, so you must win 25% of the time to be profitable. If your current hand has more than 25% equity against your opponent's perceived range, call.
Preflop Pot Odds
Preflop, you raise to 3bb and the button 3bets to 9bb. You must decide how to act. In situations like these, we can actually use pot odds to assist our decision-making.
This pot is:
(our open+3bet size+small blind+big blind)
(3bb+9bb+0.5bb+1bb)
= 13.5
This means we must call 6bb to win a pot of 13.5bb, which requires 30.7% equity against the 3bettor's range.
Three additional factors must be considered:
Being out of position on our opponent makes it harder to realize our hand's equity, as he can use his position to put us in tough spots. To profitably continue against villain's hand range, we should add 7% to our equity.
Implied Odds / Reverse Implied Odds: The ability to win or lose significantly more post-flop (than pre-flop) based on our remaining stack.
While statistics on 3bet stats can be gained with a large enough sample size (i.e. 8% 3bet stat from button), the numbers don't tell us which 8% of hands villain could be 3betting with. Both polarized and depolarized charts below show 8% of possible hands.
7.4% of hands are depolarized.
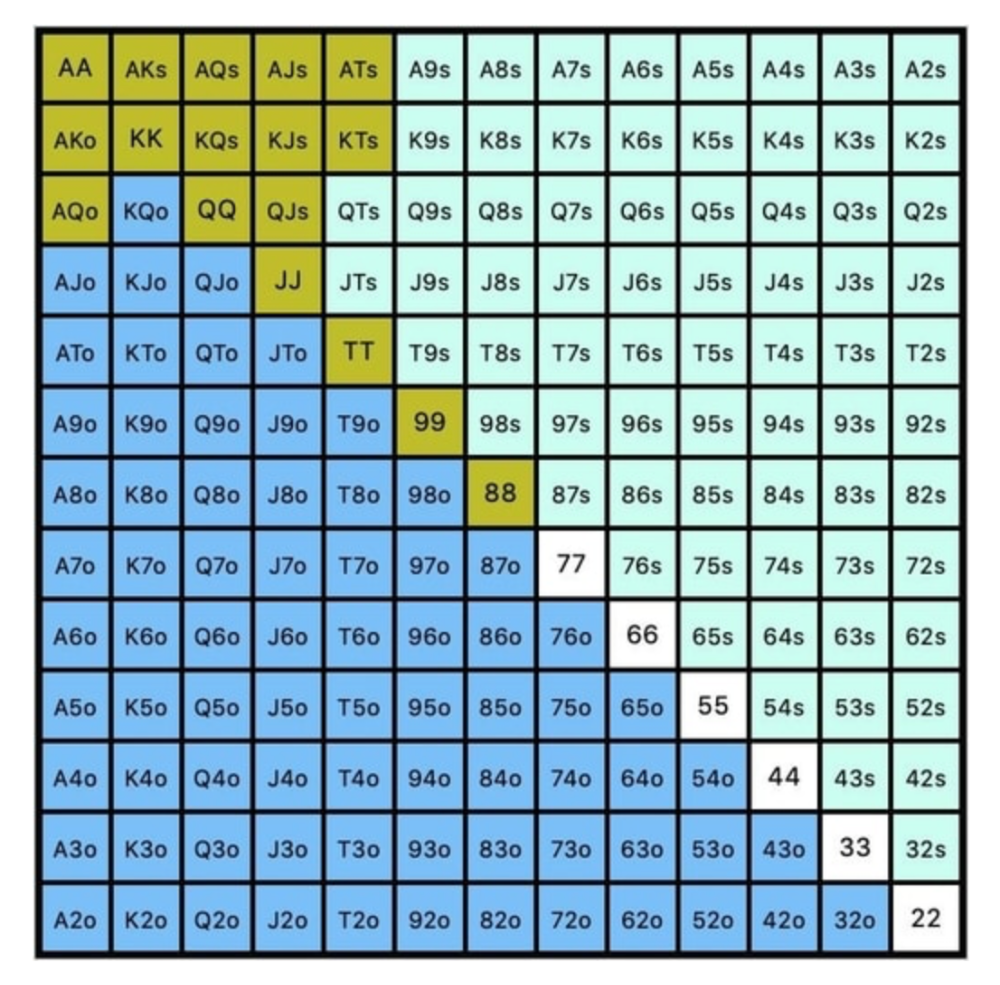
Polarized Hand range (7.54%):
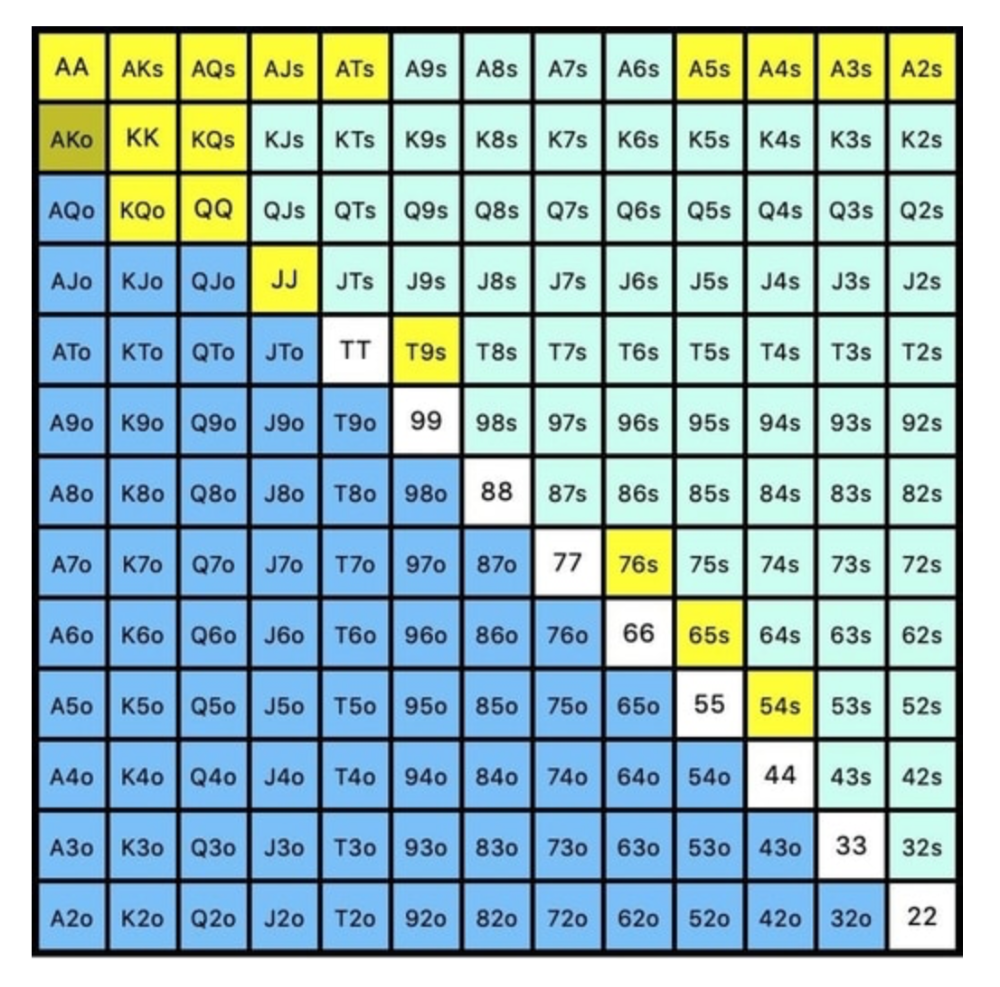
Each hand range has different contents. We don't know if he 3bets some hands and calls or folds others.
Using an exploitable strategy can help you play a hand range correctly. The next GTO concept will make things easier.
3. Minimum Defense Frequency:
This concept refers to the % of our range we must continue with (by calling or raising) to avoid being exploited by our opponents. This concept is most often used off-table and is difficult to apply in-game.
These beginner GTO concepts will help your decision-making during a hand, especially against aggressive opponents.
MDF formula:
MDF = POT SIZE/(POT SIZE+BET SIZE)
Here's a poker GTO chart of common bet sizes and minimum defense frequency.
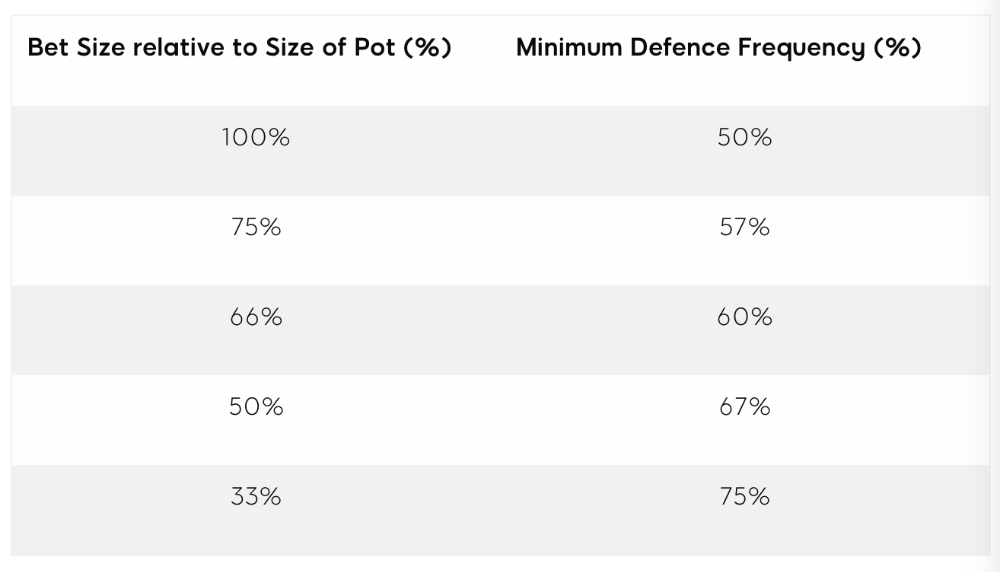
Take the number of hand combos in your starting hand range and use the MDF to determine which hands to continue with. Choose hands with the most playability and equity against your opponent's betting range.
Say you open-raise HJ and BB calls. Qh9h6c flop. Your opponent leads you for a half-pot bet. MDF suggests keeping 67% of our range.
Using the above starting hand chart, we can determine that the HJ opens 254 combos:
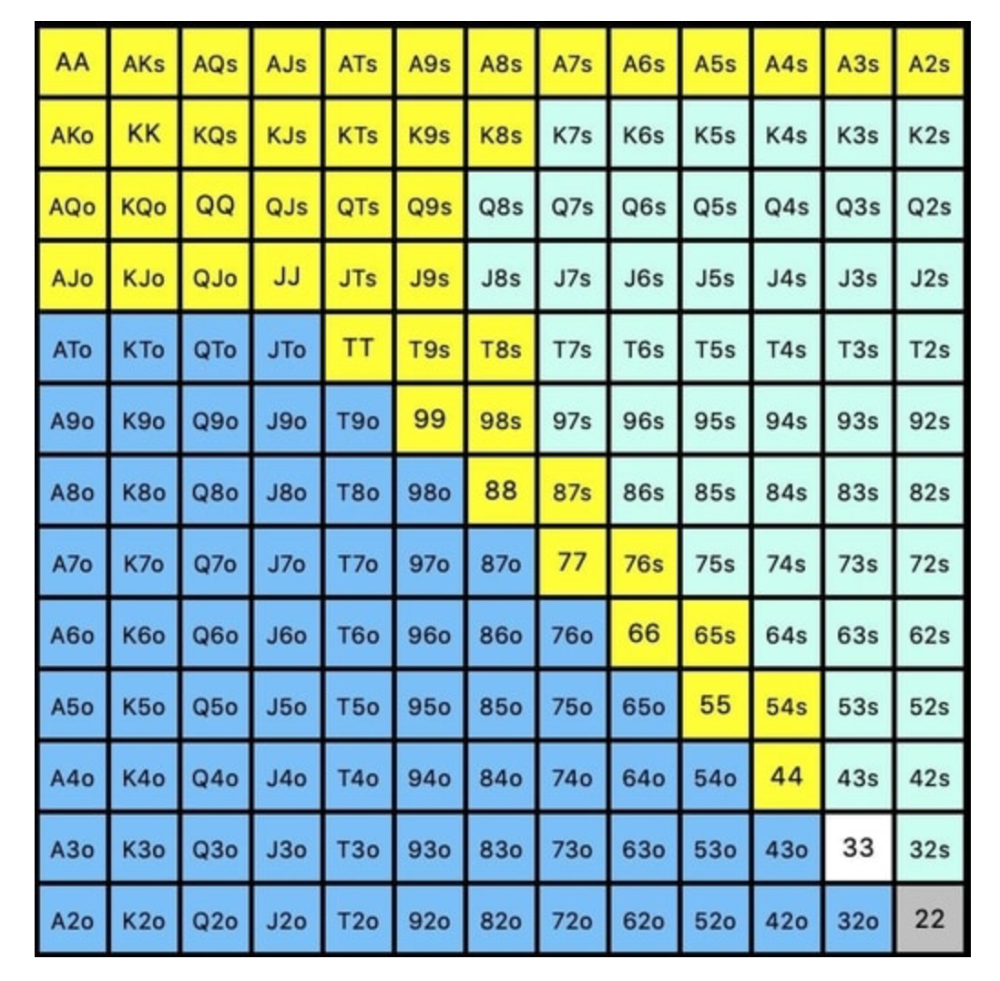
We must defend 67% of these hands, or 170 combos, according to MDF. Hands we should keep include:
Flush draws
Open-Ended Straight Draws
Gut-Shot Straight Draws
Overcards
Any Pair or better
So, our flop continuing range could be:
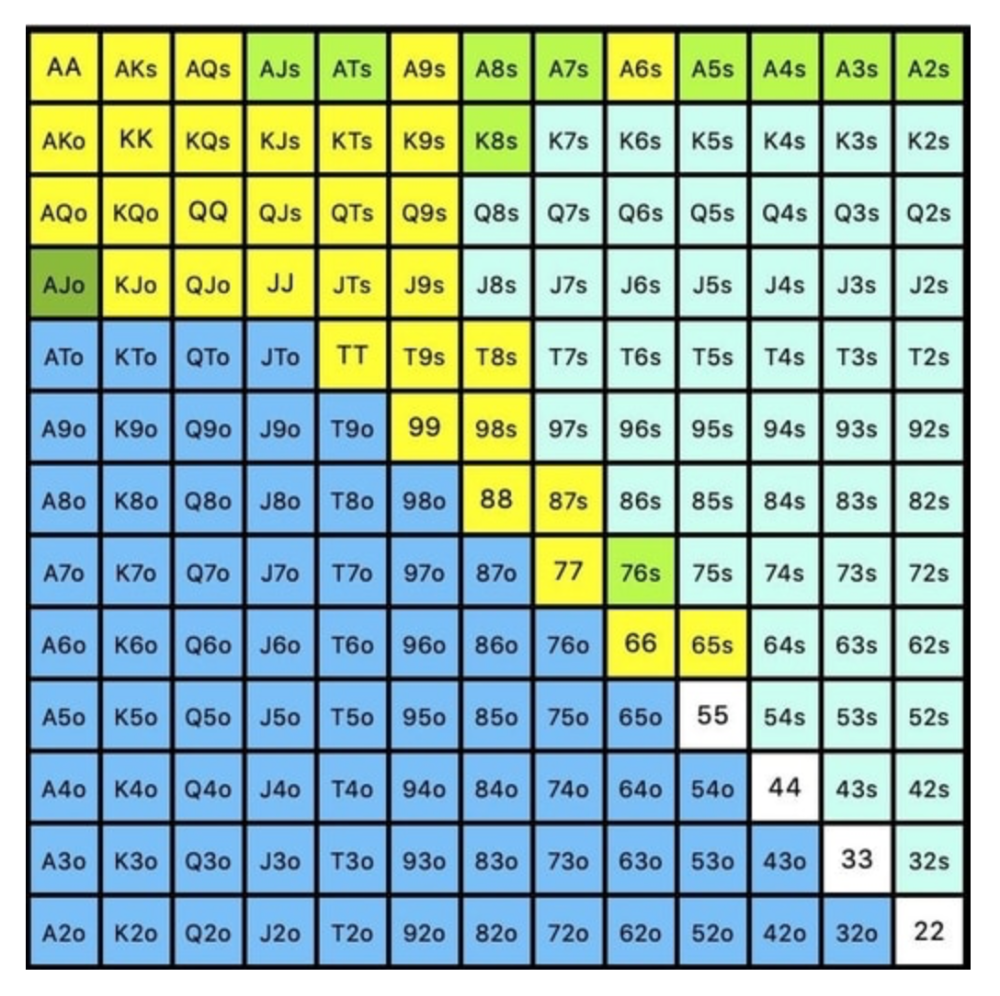
Some highlights:
Fours and fives have little chance of improving on the turn or river.
We only continue with AX hearts (with a flush draw) without a pair or better.
We'll also include 4 AJo combos, all of which have the Ace of hearts, and AcJh, which can block a backdoor nut flush combo.
Let's assume all these hands are called and the turn is blank (2 of spades). Opponent bets full-pot. MDF says we must defend 50% of our flop continuing range, or 85 of 170 combos, to be unexploitable. This strategy includes our best flush draws, straight draws, and made hands.
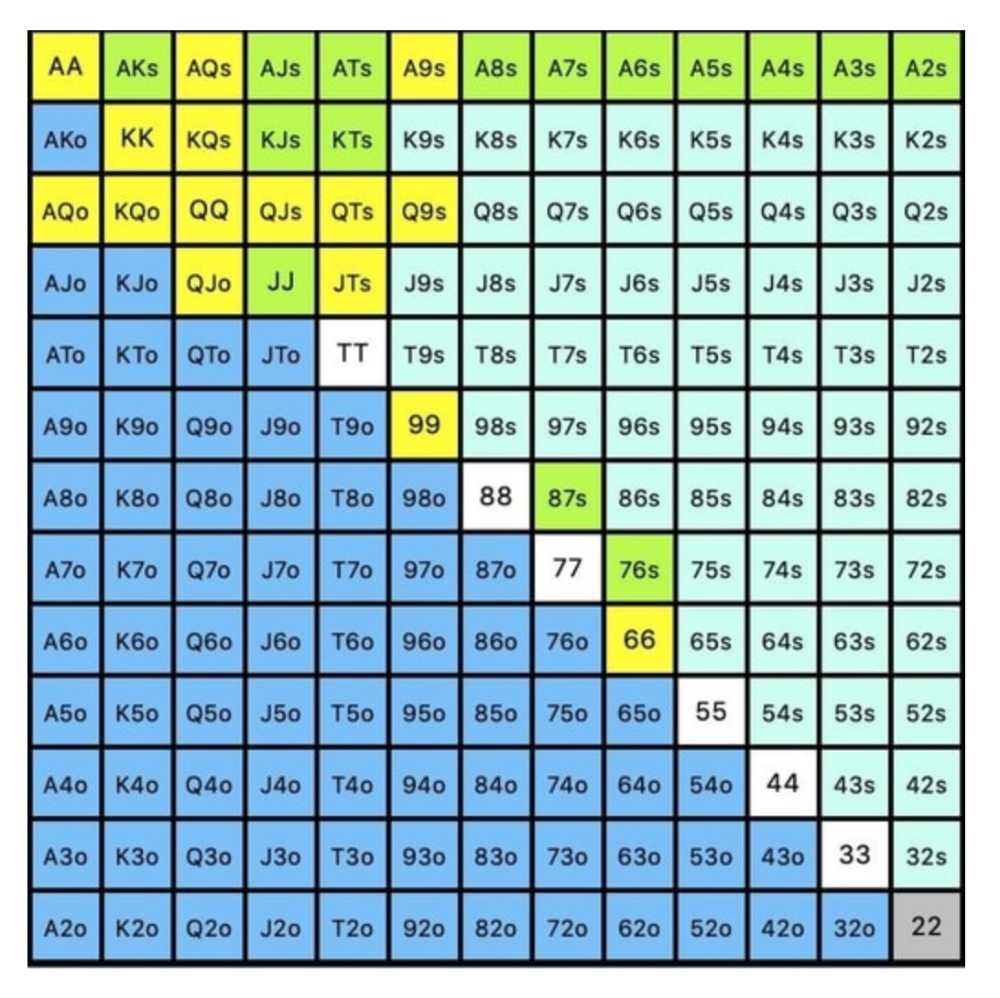
Here, we keep combining:
Nut flush draws
Pair + flush draws
GS + flush draws
Second Pair, Top Kicker+
One combo of JJ that doesn’t block the flush draw or backdoor flush draw.
On the river, we can fold our missed draws and keep our best made hands. When calling with weaker hands, consider blocker effects and card removal to avoid overcalling and decide which combos to continue.
4. Poker GTO Bet Sizing
To avoid being exploited, balance your bluffs and value bets. Your betting range depends on how much you bet (in relation to the pot). This concept only applies on the river, as draws (bluffs) on the flop and turn still have equity (and are therefore total bluffs).
On the flop, you want a 2:1 bluff-to-value-bet ratio. On the flop, there won't be as many made hands as on the river, and your bluffs will usually contain equity. The turn should have a "bluffing" ratio of 1:1. Use the chart below to determine GTO river bluff frequencies (relative to your bet size):
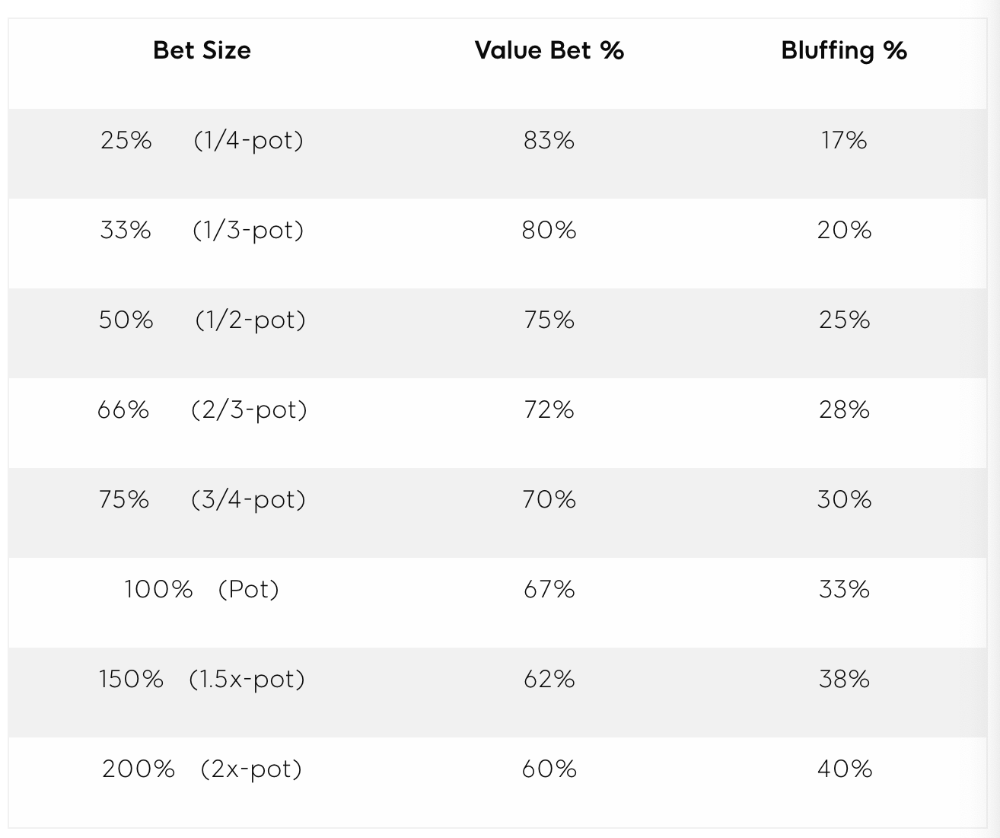
This chart relates to your opponent's pot odds. If you bet 50% pot, your opponent gets 3:1 odds and must win 25% of the time to call. Poker GTO theory suggests including 25% bluff combinations in your betting range so you're indifferent to your opponent calling or folding.
Best river bluffs don't block hands you want your opponent to have (or not have). For example, betting with missed Ace-high flush draws is often a mistake because you block a missed flush draw you want your opponent to have when bluffing on the river (meaning that it would subsequently be less likely he would have it, if you held two of the flush draw cards). Ace-high usually has some river showdown value.
If you had a 3-flush on the river and wanted to raise, you could bluff raise with AX combos holding the bluff suit Ace. Blocking the nut flush prevents your opponent from using that combo.
5. Bet Sizes and Frequency
GTO beginner strategies aren't just bluffs and value bets. They show how often and how much to bet in certain spots. Top players have benefited greatly from poker solvers, which we'll discuss next.
GTO Poker Software
In recent years, various poker GTO solvers have been released to help beginner, intermediate, and advanced players play balanced/GTO poker in various situations.
PokerSnowie and PioSolver are popular GTO and poker study programs.
While you can't compute players' hand ranges and what hands to bet or check with in real time, studying GTO play strategies with these programs will pay off. It will improve your poker thinking and understanding.
Solvers can help you balance ranges, choose optimal bet sizes, and master cbet frequencies.
GTO Poker Tournament
Late-stage tournaments have shorter stacks than cash games. In order to follow GTO poker guidelines, Nash charts have been created, tweaked, and used for many years (and also when to call, depending on what number of big blinds you have when you find yourself shortstacked).
The charts are for heads-up push/fold. In a multi-player game, the "pusher" chart can only be used if play is folded to you in the small blind. The "caller" chart can only be used if you're in the big blind and assumes a small blind "pusher" (with a much wider range than if a player in another position was open-shoving).
Divide the pusher chart's numbers by 2 to see which hand to use from the Button. Divide the original chart numbers by 4 to find the CO's pushing range. Some of the figures will be impossible to calculate accurately for the CO or positions to the right of the blinds because the chart's highest figure is "20+" big blinds, which is also used for a wide range of hands in the push chart.
Both of the GTO charts below are ideal for heads-up play, but exploitable HU shortstack strategies can lead to more +EV decisions against certain opponents. Following the charts will make your play GTO and unexploitable.
Poker pro Max Silver created the GTO push/fold software SnapShove. (It's accessible online at www.snapshove.com or as iOS or Android apps.)
Players can access GTO shove range examples in the full version. (You can customize the number of big blinds you have, your position, the size of the ante, and many other options.)
In Conclusion
Due to the constantly changing poker landscape, players are always improving their skills. Exploitable strategies often yield higher profit margins than GTO-based approaches, but knowing GTO beginner and advanced concepts can give you an edge for a few reasons.
It creates a solid gameplay base.
Having a baseline makes it easier to exploit certain villains.
You can avoid leveling wars with your opponents by making sound poker decisions based on GTO strategy.
It doesn't require assuming opponents' play styles.
Not results-oriented.
This is just the beginning of GTO and poker theory. Consider investing in the GTO poker solver software listed above to improve your game.
