Key Takeaways:

Another hack. This time was different. This is a doozy.

Why? Nomad got exploited for $190m. It was crypto's 5th-biggest hack. Ouch.

It wasn't hackers, but random folks. What happened:

A Nomad smart contract flaw was discovered. They couldn't drain the funds at once, so they tried numerous transactions. Rookie!

People noticed and copied the attack.

They just needed to discover a working transaction, substitute the other person's address with theirs, and run it.

In a two-and-a-half-hour attack, $190M was siphoned from Nomad Bridge.

Nomad is a novel approach to blockchain interoperability that leverages an optimistic mechanism to increase the security of cross-chain communication.  — nomad.xyz

This hack was permissionless, therefore anyone could participate.

After the fatal blow, people fought over the scraps.

Cross-chain bridges remain a DeFi weakness and exploit target. When they collapse, it's typically total.

$190M...gobbled.

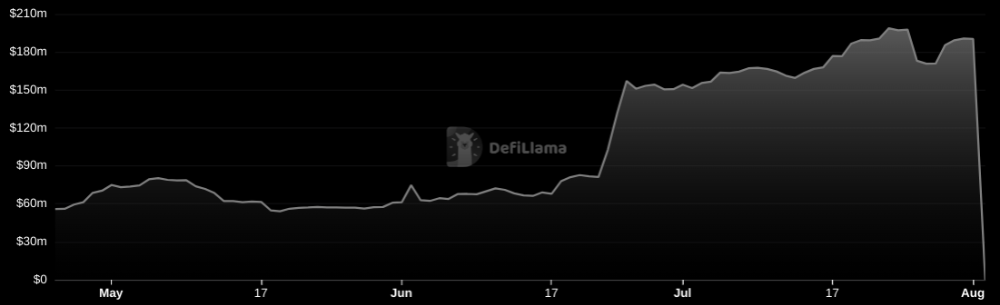
Unbacked assets are hurting Nomad-dependent chains. Moonbeam, EVMOS, and Milkomeda's TVLs dropped.

This incident is every-man-for-himself, although numerous whitehats exploited the issue... 

But what triggered the feeding frenzy?

How did so many pick the bones?

After a normal upgrade in June, the bridge's Replica contract was initialized with a severe security issue. The  0x00 address was a trusted root, therefore all messages were valid by default.

After a botched first attempt (costing $350k in gas), the original attacker's exploit tx called process() without first 'proving' its validity.

The process() function executes all cross-chain messages and checks the merkle root of all messages (line 185).

The upgrade caused transactions with a'messages' value of 0 (invalid, according to old logic) to be read by default as 0x00, a trusted root, passing validation as 'proven'

Any process() calls were valid. In reality, a more sophisticated exploiter may have designed a contract to drain the whole bridge.

Copycat attackers simply copied/pasted the same process() function call using Etherscan, substituting their address.

The incident was a wild combination of crowdhacking, whitehat activities, and MEV-bot (Maximal Extractable Value) mayhem.

For example, 🍉🍉🍉. eth stole $4M from the bridge, but claims to be whitehat.

Others stood out for the wrong reasons. Repeat criminal Rari Capital (Artibrum) exploited over $3M in stablecoins, which moved to Tornado Cash.

The top three exploiters (with 95M between them) are:

$47M: 0x56D8B635A7C88Fd1104D23d632AF40c1C3Aac4e3

$40M: 0xBF293D5138a2a1BA407B43672643434C43827179

$8M: 0xB5C55f76f90Cc528B2609109Ca14d8d84593590E

Here's a list of all the exploiters:

The project conducted a Quantstamp audit in June; QSP-19 foreshadowed a similar problem.

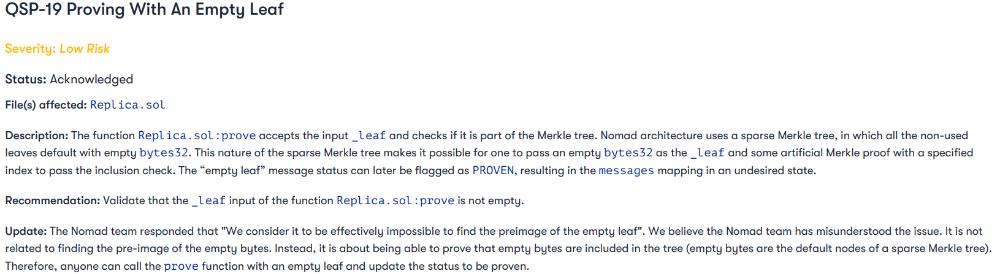
The auditor's comments that "We feel the Nomad team misinterpreted the issue" speak to a troubling attitude towards security that the project's "Long-Term Security" plan appears to confirm:

Concerns were raised about the team's response time to a live, public exploit; the team's official acknowledgement came three hours later.

"Removing the Replica contract as owner" stopped the exploit, but it was too late to preserve the cash.

Closed blockchain systems are only as strong as their weakest link.

The Harmony network is in turmoil after its bridge was attacked and lost $100M in late June.

What's next for Nomad's ecosystems?

Moonbeam's TVL is now $135M, EVMOS's is $3M, and Milkomeda's is $20M.

Loss of confidence may do more damage than $190M.

Cross-chain infrastructure is difficult to secure in a new, experimental sector. Bridge attacks can pollute an entire ecosystem or more.

Nomadic liquidity has no permanent home, so consumers will always migrate in pursuit of the "next big thing" and get stung when attentiveness wanes.

DeFi still has easy prey...

Sources: rekt.news & The Milk Road.

James Howells lost 8,000 bitcoins. He has $11 million to get them back.

His life altered when he threw out an iPhone-sized hard drive.

Howells, from the city of Newport in southern Wales, had two identical laptop hard drives squirreled away in a drawer in 2013. One was blank; the other had 8,000 bitcoins, currently worth around $181 million.

He wanted to toss out the blank one, but the drive containing the Bitcoin went to the dump.

He's determined to reclaim his 2009 stash.

Howells, 36, wants to arrange a high-tech treasure hunt for bitcoins. He can't enter the landfill.

Newport's city council has rebuffed Howells' requests to dig for his hard drive for almost a decade, stating it would be expensive and environmentally destructive.

I got an early look at his $11 million idea to search 110,000 tons of trash. He expects submitting it to the council would convince it to let him recover the hard disk.

110,000 tons of trash, 1 hard drive

Finding a hard disk among heaps of trash may seem Herculean.

Former IT worker Howells claims it's possible with human sorters, robot dogs, and an AI-powered computer taught to find hard drives on a conveyor belt.

His idea has two versions, depending on how much of the landfill he can search.

His most elaborate solution would take three years and cost $11 million to sort 100,000 metric tons of waste. Scaled-down version costs $6 million and takes 18 months.

He's created a team of eight professionals in AI-powered sorting, landfill excavation, garbage management, and data extraction, including one who recovered Columbia's black box data.

The specialists and their companies would be paid a bonus if they successfully recovered the bitcoin stash.

Howells: "We're trying to commercialize this project."

Howells claimed rubbish would be dug up by machines and sorted near the landfill.

Human pickers and a Max-AI machine would sort it. The machine resembles a scanner on a conveyor belt.

Remi Le Grand of Max-AI told us it will train AI to recognize Howells-like hard drives. A robot arm would select candidates.

Howells has added security charges to his scheme because he fears people would steal the hard drive.

He's budgeted for 24-hour CCTV cameras and two robotic "Spot" canines from Boston Dynamics that would patrol at night and look for his hard drive by day.

Howells said his crew met in May at the Celtic Manor Resort outside Newport for a pitch rehearsal.

Richard Hammond's narrative swings from banal to epic.

Richard Hammond filmed the meeting and created a YouTube documentary on Howells.

Hammond said of Howells' squad, "They're committed and believe in him and the idea."

Hammond: "It goes from banal to gigantic." "If I were in his position, I wouldn't have the strength to answer the door."

Howells said trash would be cleaned and repurposed after excavation. Reburying the rest.

"We won't pollute," he declared. "We aim to make everything better."

After the project is finished, he hopes to develop a solar or wind farm on the dump site. The council is unlikely to accept his vision soon.

A council representative told us, "Mr. Howells can't convince us of anything." "His suggestions constitute a significant ecological danger, which we can't tolerate and are forbidden by our permit."

Will the recovered hard drive work?

The "platter" is a glass or metal disc that holds the hard drive's data. Howells estimates 80% to 90% of the data will be recoverable if the platter isn't damaged.

Phil Bridge, a data-recovery expert who consulted Howells, confirmed these numbers.

If the platter is broken, Bridge adds, data recovery is unlikely.

Bridge says he was intrigued by the proposal. "It's an intriguing case," he added. Helping him get it back and proving everyone incorrect would be a great success story.

Who'd pay?

Swiss and German venture investors Hanspeter Jaberg and Karl Wendeborn told us they would fund the project if Howells received council permission.

Jaberg: "It's a needle in a haystack and a high-risk investment."

Howells said he had no contract with potential backers but had discussed the proposal in Zoom meetings. "Until Newport City Council gives me something in writing, I can't commit," he added.

Suppose he finds the bitcoins.

Howells said he would keep 30% of the data, worth $54 million, if he could retrieve it.

A third would go to the recovery team, 30% to investors, and the remainder to local purposes, including gifting £50 ($61) in bitcoin to each of Newport's 150,000 citizens.

Howells said he opted to spend extra money on "professional firms" to help convince the council.

What if the council doesn't approve?

If Howells can't win the council's support, he'll sue, claiming its actions constitute a "illegal embargo" on the hard drive. "I've avoided that path because I didn't want to cause complications," he stated. I wanted to cooperate with Newport's council.

Howells never met with the council face-to-face. He mentioned he had a 20-minute Zoom meeting in May 2021 but thought his new business strategy would help.

He met with Jessica Morden on June 24. Morden's office confirmed meeting.

After telling the council about his proposal, he can only wait. "I've never been happier," he said. This is our most professional operation, with the best employees.

The "crypto proponent" buys bitcoin every month and sells it for cash.

Howells tries not to think about what he'd do with his part of the money if the hard disk is found functional. "Otherwise, you'll go mad," he added.

This post is a summary. Read the full article here.

Research on preventing disease, extending life, and caring for your body from the inside out

Grapefruit and pomegranates aren't on the list, so ignore that. Mostly, I enjoyed the visual, but those fruits are healthful, too.

15 (or 17 if you consider the photo) different foods a day sounds like a lot. If you're not used to it  — it is.

These lists don't aim for perfection. Instead, use this article and the science below to eat more of these foods. If you can eat 5 foods one day and 5 the next, you're doing well. This list should be customized to your requirements and preferences.

“Every time you eat or drink, you are either feeding disease or fighting it” -Heather Morgan.

The 15 Foods That You Should Consume Daily and Why:

1. Dark/Red Berries

(blueberries, blackberries, acai, goji, cherries, strawberries, raspberries)

The 2010 Global Burden of Disease Study is the greatest definitive analysis of death and disease risk factors in history. They found the primary cause of both death, disability, and disease inside the United States was diet.

Not eating enough fruit, and specifically berries, was one of the best predictors of disease (1).

What's special about berries? It's their color! Berries have the most antioxidants of any fruit, second only to spices. The American Cancer Society found that those who ate the most berries were less likely to die of cardiovascular disease.

2. Beans

Soybeans, black beans, kidney beans, lentils, split peas, chickpeas.

Beans are one of the most important predictors of survival in older people, according to global research (2).

For every 20 grams (2 tablespoons) of beans consumed daily, the risk of death is reduced by 8%.

Soybeans and soy foods are high in phytoestrogen, which reduces breast and prostate cancer risks. Phytoestrogen blocks the receptors' access to true estrogen, mitigating the effects of weight gain, dairy (high in estrogen), and hormonal fluctuations (3).

3. Nuts

(almonds, walnuts, pecans, pistachios, Brazil nuts, cashews, hazelnuts, macadamia nuts)

Eating a handful of nuts every day reduces the risk of chronic diseases like heart disease and diabetes. Nuts also reduce oxidation, blood sugar, and LDL (bad) cholesterol, improving arterial function (4).

Despite their high-fat content, studies have linked daily nut consumption to a slimmer waistline and a lower risk of obesity (5).

4. Flaxseed

(milled flaxseed)

2013 research found that ground flaxseed had one of the strongest anti-hypertensive effects of any food. A few tablespoons (added to a smoothie or baked goods) lowered blood pressure and stroke risk 23 times more than daily aerobic exercise (6).

Flax shouldn't replace exercise, but its nutritional punch is worth adding to your diet.

5. Other seeds

(chia seeds, hemp seeds, pumpkin seeds, sesame seeds, fennel seeds)

Seeds are high in fiber and omega-3 fats and can be added to most dishes without being noticed.

When eaten with or after a meal, chia seeds moderate blood sugar and reduce inflammatory chemicals in the blood (7). Overall, a great daily addition.

6. Dates

Dates are one of the world's highest sugar foods, with 80% sugar by weight. Pure cake frosting is 60%, maple syrup is 66%, and cotton-candy jelly beans are 70%.

Despite their high sugar content, dates have a low glycemic index, meaning they don't affect blood sugar levels dramatically. They also improve triglyceride and antioxidant stress levels (8).

Dates are a great source of energy and contain high levels of dietary fiber and polyphenols, making 3-10 dates a great way to fight disease, support gut health with prebiotics, and satisfy a sweet tooth (9).

7. Cruciferous Veggies

(broccoli, Brussel sprouts, horseradish, kale, cauliflower, cabbage, boy choy, arugula, radishes, turnip greens)

Cruciferous vegetables contain an active ingredient that makes them disease-fighting powerhouses. Sulforaphane protects our brain, eyesight, against free radicals and environmental hazards, and treats and prevents cancer (10).

Unless you eat raw cruciferous vegetables daily, you won't get enough sulforaphane (and thus, its protective nutritional benefits). Cooking destroys the enzyme needed to create this super-compound.

If you chop broccoli, cauliflower, or turnip greens and let them sit for 45 minutes before cooking them, the enzyme will have had enough time to work its sulforaphane magic, allowing the vegetables to retain the same nutritional value as if eaten raw. Crazy, right? For more on this, see What Chopping Your Vegetables Has to Do with Fighting Cancer.

8. Whole grains

(barley, brown rice, quinoa, oats, millet, popcorn, whole-wheat pasta, wild rice)

Whole-grains are one of the healthiest ways to consume your daily carbs and help maintain healthy gut flora.

This happens when fibre is broken down in the colon and starts a chain reaction, releasing beneficial substances into the bloodstream and reducing the risk of Type 2 Diabetes and inflammation (11).

9. Spices

(turmeric, cumin, cinnamon, ginger, saffron, cloves, cardamom, chili powder, nutmeg, coriander)

7% of a person's cells will have DNA damage. This damage is caused by tiny breaks in our DNA caused by factors like free-radical exposure.

Free radicals cause mutations that damage lipids, proteins, and DNA, increasing the risk of disease and cancer. Free radicals are unavoidable because they result from cellular metabolism, but they can be avoided by consuming anti-oxidant and detoxifying foods.

Including spices and herbs like rosemary or ginger in our diet may cut DNA damage by 25%. Yes, this damage can be improved through diet. Turmeric worked better at a lower dose (just a pinch, daily). For maximum free-radical fighting (and anti-inflammatory) effectiveness, use 1.5 tablespoons of similar spices (12).

10. Leafy greens

(spinach, collard greens, lettuce, other salad greens, swiss chard)

Studies show that people who eat more leafy greens perform better on cognitive tests and slow brain aging by a year or two (13).

As we age, blood flow to the brain drops due to a decrease in nitric oxide, which prevents blood vessels from dilatation. Daily consumption of nitrate-rich vegetables like spinach and swiss chard may prevent dementia and Alzheimer's.

11. Fermented foods

(sauerkraut, tempeh, kombucha, plant-based kefir)

Miso, kimchi, and sauerkraut contain probiotics that support gut microbiome.

Probiotics balance the good and bad bacteria in our bodies and offer other benefits. Fermenting fruits and vegetables increases their antioxidant and vitamin content, preventing disease in multiple ways (14).

12. Sea vegetables

(seaweed, nori, dulse flakes)

A population study found that eating one sheet of nori seaweed per day may cut breast cancer risk by more than half (15).

Seaweed and sea vegetables may help moderate estrogen levels in the metabolism, reducing cancer and disease risk.

Sea vegetables make up 30% of the world's edible plants and contain unique phytonutrients. A teaspoon of these super sea-foods on your dinner will help fight disease from the inside out.

13. Water

I'm less concerned about whether you consider water food than whether you drink enough. If this list were ranked by what single item led to the best health outcomes, water would be first.

Research shows that people who drink 5 or more glasses of water per day have a 50% lower risk of dying from heart disease than those who drink 2 or less (16).

Drinking enough water boosts energy, improves skin, mental health, and digestion, and reduces the risk of various health issues, including obesity.

14. Tea

All tea consumption is linked to a lower risk of stroke, heart disease, and early death, with green tea leading for antioxidant content and immediate health benefits.

Green tea leaves may also be able to interfere with each stage of cancer formation, from the growth of the first mutated cell to the spread and progression of cancer in the body. Green tea is a quick and easy way to support your long-term and short-term health (17).

15. Supplemental B12 vitamin

B12, or cobalamin, is a vitamin responsible for cell metabolism. Not getting enough B12 can have serious consequences.

Historically, eating vegetables from untreated soil helped humans maintain their vitamin B12 levels. Due to modern sanitization, our farming soil lacks B12.

B12 is often cited as a problem only for vegetarians and vegans (as animals we eat are given B12 supplements before slaughter), but recent studies have found that plant-based eaters have lower B12 deficiency rates than any other diet (18).

Article Sources:

1. The Global Burden of Disease Study 2010 (GBD 2010)

2. I. Darmadi-Blackberry, M. Wahlqvist, A. Kouris-Blazos, et al. Legumes: the most important dietary predictor of survival in older people of different ethnicities. Asia Pac J Clin Nutr. 2004;13(2):217–20.

3. Guha N, Kwan ML, Quesenberry CP Jr, Weltzien EK, Castillo AL, Caan BJ. Soy isoflavones and risk of cancer recurrence in a cohort of breast cancer survivors: the Life After Cancer Epidemiology study. Breast Cancer Res Treat. 2009 Nov;118(2):395–405.

4. Y. Bao, J. Han, F. B. Hu, E. L. Giovannucci, M. J. Stampfer, W. C. Willett, C. S. Fuchs. Association of nut consumption with total and cause-specific mortality. N. Engl. J. Med. 2013 369(21):2001–2011.

5. V. Vadivel, C. N. Kunyanga, H. K. Biesalski. Health benefits of nut consumption with special reference to body weight control. Nutrition 2012 28(11–12):1089–1097.

6. D Rodriguez-Leyva, W Weighell, A L Edel,R LaVallee, E Dibrov,R Pinneker, T G Maddaford, B Ramjiawan, M Aliani, R Guzman R, G N Pierce. Potent antihypertensive action of dietary flaxseed in hypertensive patients. Hypertension. 2013 Dec;62(6):1081–9. doi: 10.1161/HYPERTENSIONAHA.113.02094.

7. Vuksan V, Jenkins AL, Dias AG, Lee AS, Jovanovski E, Rogovik AL, Hanna A. Reduction in postprandial glucose excursion and prolongation of satiety: possible explanation of the long-term effects of whole grain Salba (Salvia Hispanica L.). Eur J Clin Nutr. 2010 Apr;64(4):436–8. doi: 10.1038/ejcn.2009.159. Epub 2010 Jan 20. PMID: 20087375.

8. W. Rock, M. Rosenblat, H. Borochov-Neori, N. Volkova, S. Judeinstein, M. Elias, and M. Aviram. Effects of date (Phoenix dactylifera L., Medjool or Hallawi Variety) consumption by healthy subjects on serum glucose and lipid levels and on serum oxidative status: a pilot study. J. Agric. Food. Chem., 57(17):8010{8017, 2009.

9. Eid N, Enani S, Walton G, et al. The impact of date palm fruits and their component polyphenols, on gut microbial ecology, bacterial metabolites and colon cancer cell proliferation. J Nutr Sci. 2014;3:e46.

10. Li Y, Zhang T, Korkaya H, Liu S, Lee HF, Newman B, Yu Y, Clouthier SG, Schwartz SJ, Wicha MS, Sun D. Sulforaphane, a Dietary Component of Broccoli/Broccoli Sprouts, Inhibits Breast Cancer Stem Cells. Clin Cancer Res. 2010 May 1;16(9):2580–90.

11. Lappi J, Kolehmainen M, Mykkänen H, Poutanen K. Do large intestinal events explain the protective effects of whole grain foods against type 2 diabetes? Crit Rev Food Sci Nutr. 2013;53(6):631–40.

12. S. S. Percival, J. P. V. Heuvel, C. J. Nieves, C. Montero, A. J. Migliaccio, J. Meadors. Bioavailability of Herbs and Spices in Humans as Determined by ex vivo Inflammatory Suppression and DNA Strand Breaks. J Am Coll Nutr. 2012 31(4):288–294.

13. Nurk E, Refsum H, Drevon CA, et al. Cognitive performance among the elderly in relation to the intake of plant foods. The Hordaland Health Study. Br J Nutr. 2010;104(8):1190–201.

14. Melini, F.; Melini, V.; Luziatelli, F.; Ficca, A.G.; Ruzzi, M. Health-Promoting Components in Fermented Foods: An Up-to-Date Systematic Review. Nutrients2019, 11, 1189.

15. H. Funahashi, T. Imai, T. Mase, M. Sekiya, K. Yokoi, H. Hayashi, A. Shibata, T. Hayashi, M. Nishikawa, N. Suda, Y. Hibi, Y. Mizuno, K. Tsukamura, A. Hayakawa, S. Tanuma. Seaweed prevents breast cancer? Jpn. J. Cancer Res. 2001 92(5):483–487.

16. Chan J, Knutsen SF, Blix GG, Lee JW, Fraser GE. Water, other fluids, and fatal coronary heart disease: the Adventist Health Study. Am J Epidemiol. 2002 May 1;155(9):827–33. doi: 10.1093/aje/155.9.827. PMID: 11978586.

17. Fujiki H, Imai K, Nakachi K, Shimizu M, Moriwaki H, Suganuma M. Challenging the effectiveness of green tea in primary and tertiary cancer prevention. J Cancer Res Clin Oncol. 2012 Aug;138(8):1259–70.

18. Damayanti, D., Jaceldo-Siegl, K., Beeson, W. L., Fraser, G., Oda, K., & Haddad, E. H. (2018). Foods and Supplements Associated with Vitamin B12Biomarkers among Vegetarian and Non-Vegetarian Participants of the Adventist Health Study-2 (AHS-2) Calibration Study. Nutrients, 10(6), 722. doi:10.3390/nu10060722

The trick Notion could use is simply Facebook-ing the hell out of them.

*Time travel to fifteen years ago.* Future-Me: “Hey! What are you up to?” Old-Me: “I am proofreading an article. It’s taking a few hours, but I will be done soon.” Future-Me: “You know, in the future, you will be using a google chrome plugin called Grammarly that will help you easily proofread articles in half that time.” Old-Me: “What is… Google Chrome?” Future-Me: “Gosh…”

I love Grammarly. It’s one of those products that I personally feel the effects of. I mean, Space X is a great company. But I am not a rocket writing this article in space (or am I?)…

No, I’m not. So I don’t personally feel a connection to Space X. So, if a company collapse occurs in the morning, I might write about it. But I will have zero emotions regarding it.

Yet, if Grammarly fails tomorrow, I will feel 1% emotionally distressed. So looking at the title of this article, you’d realize that I am betting against them. This is how much I believe in the critical business model that’s taking over the world, the one of Notion.

Notion How frequently do you go through your notes?

Grammarly is everywhere, which helps its success. Grammarly is available when you update LinkedIn on Chrome. Grammarly prevents errors in Google Docs.

My internal concentration isn't apparent in the previous paragraph. Not Grammarly. I should have used Chrome to make a Google doc and LinkedIn update. Without this base, Grammarly will be useless.

So, welcome to this business essay.

• Grammarly provides a solution.

• Another issue is resolved by Jasper.

• Your entire existence is supposed to be contained within Notion.

New Google Chrome is offline. It's an all-purpose notepad (in the near future.)

• How should I start my blog? Enter it in Note.

• an update on LinkedIn? If you mention it, it might be automatically uploaded there (with little help from another app.)

• An advanced thesis? You can brainstorm it with your coworkers.

This ad sounds great! I won't cry if Notion dies tomorrow.

I'll reread the following passages to illustrate why I think Notion could kill Grammarly and Jasper.

Notion is a fantastic app that incubates your work.

Smartly, they began with note-taking.

Hopefully, your work will be on Notion. Grammarly and Jasper are still must-haves.

Grammarly will proofread your typing while Jasper helps with copywriting and AI picture development.

They're the best, therefore you'll need them. Correct? Nah.

Notion might bombard them with Facebook posts.

Notion: “Hi Grammarly, do you want to sell your product to us?” Grammarly: “Dude, we are more valuable than you are. We’ve even raised $400m, while you raised $342m. Our last valuation round put us at $13 billion, while yours put you at $10 billion. Go to hell.” Notion: “Okay, we’ll speak again in five years.”

Notion: “Jasper, wanna sell?” Jasper: “Nah, we’re deep into AI and the field. You can’t compete with our people.” Notion: “How about you either sell or you turn into a Snapchat case?” Jasper: “…”

Notion is your home. Grammarly is your neighbor. Your track is Jasper.

What if you grew enough vegetables in your backyard to avoid the supermarket? No more visits.

What if your home had a beautiful treadmill? You won't rush outside as much (I disagree with my own metaphor). (You get it.)

It's Facebooking. Instagram Stories reduced your Snapchat usage. Notion will reduce your need to use Grammarly.

The Final Piece of the AI Puzzle

Let's talk about Notion first, since you've probably read about it everywhere.

• They raised $343 million, as I previously reported, and bought four businesses

• According to Forbes, Notion will have more than 20 million users by 2022. The number of users is up from 4 million in 2020.

If raising $1.8 billion was impressive, FTX wouldn't have fallen.

This article compares the basic product to two others. Notion is a day-long app.

Notion has released Notion AI to support writers. It's early, so it's not as good as Jasper. Then-Jasper isn't now-Jasper. In five years, Notion AI will be different.

With hard work, they may construct a Jasper-like writing assistant. They have resources and users.

At this point, it's all speculation. Jasper's copywriting is top-notch. Grammarly's proofreading is top-notch. Businesses are constrained by user activities.

If Notion's future business movements are strategic, they might become a blue ocean shark (or get acquired by an unbelievable amount.)

I love business mental teasers, so tell me:

• How do you feel? Are you a frequent Notion user?

• Do you dispute my position? I enjoy hearing opposing viewpoints.

Ironically, I proofread this with Grammarly.

When you stop blogging for a few weeks, your views and profits plummet.

Because you're writing fascinating posts for others. Everyone's done ithat…

If I keep writing, the graph should maintain velocity, you could say. If I wrote more, it could rise.

However, entertaining pieces still tend to roller coaster and jump.

this type of writing is like a candle. They burn out and must be replaced. You must continuously light new ones to maintain the illumination.

When you quit writing, your income stops.

A substitute

Instead of producing amusing articles, try solving people's issues. You should answer their search questions.

Here's what happens when you answer their searches.

My website's Google analytics. As a dentist, I answer oral health questions.

This chart vs. Medium is pretty glaring, right?

As of yesterday, it was averaging 15k page views each day.

How much would you make on Medium with 15k daily views?

Evergreen materials

In SEO, this is called evergreen content.

Your content is like a lush, evergreen forest, and by green I mean Benjamins.

Do you have knowledge that you can leverage? Why not help your neighbors and the world?

Answer search inquiries and help others. You'll be well rewarded.

This is better than crafting candle-like content that fizzles out quickly.

Is beauty really ephemeral like how flowers bloom? Nah, I prefer watching forests grow instead (: