More on Leadership

Caspar Mahoney
2 years ago
Changing Your Mindset From a Project to a Product
Product game mindsets? How do these vary from Project mindset?
1950s spawned the Iron Triangle. Project people everywhere know and live by it. In stakeholder meetings, it is used to stretch the timeframe, request additional money, or reduce scope.
Quality was added to this triangle as things matured.
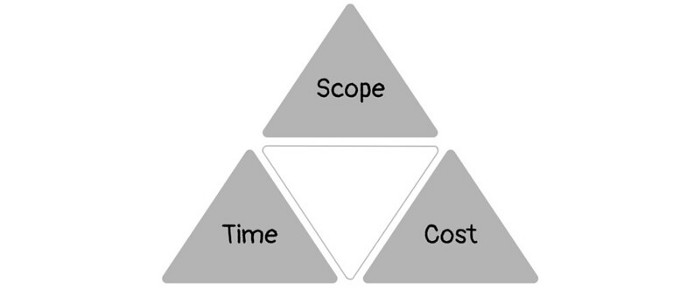
Quality was intended to be transformative, but none of these principles addressed why we conduct projects.
Value and benefits are key.
Product value is quantified by ROI, revenue, profit, savings, or other metrics. For me, every project or product delivery is about value.
Most project managers, especially those schooled 5-10 years or more ago (thousands working in huge corporations worldwide), understand the world in terms of the iron triangle. What does that imply? They worry about:
a) enough time to get the thing done.
b) have enough resources (budget) to get the thing done.
c) have enough scope to fit within (a) and (b) >> note, they never have too little scope, not that I have ever seen! although, theoretically, this could happen.
Boom—iron triangle.
To make the triangle function, project managers will utilize formal governance (Steering) to move those things. Increase money, scope, or both if time is short. Lacking funds? Increase time, scope, or both.
In current product development, shifting each item considerably may not yield value/benefit.
Even terrible. This approach will fail because it deprioritizes Value/Benefit by focusing the major stakeholders (Steering participants) and delivery team(s) on Time, Scope, and Budget restrictions.
Pre-agile, this problem was terrible. IT projects failed wildly. History is here.
Value, or benefit, is central to the product method. Product managers spend most of their time planning value-delivery paths.
Product people consider risk, schedules, scope, and budget, but value comes first. Let me illustrate.
Imagine managing internal products in an enterprise. Your core customer team needs a rapid text record of a chat to fix a problem. The consumer wants a feature/features added to a product you're producing because they think it's the greatest spot.
Project-minded, I may say;
Ok, I have budget as this is an existing project, due to run for a year. This is a new requirement to add to the features we’re already building. I think I can keep the deadline, and include this scope, as it sounds related to the feature set we’re building to give the desired result”.
This attitude repeats Scope, Time, and Budget.
Since it meets those standards, a project manager will likely approve it. If they have a backlog, they may add it and start specking it out assuming it will be built.
Instead, think like a product;
What problem does this feature idea solve? Is that problem relevant to the product I am building? Can that problem be solved quicker/better via another route ? Is it the most valuable problem to solve now? Is the problem space aligned to our current or future strategy? or do I need to alter/update the strategy?
A product mindset allows you to focus on timing, resource/cost, feasibility, feature detail, and so on after answering the aforementioned questions.
The above oversimplifies because
Leadership in discovery

Project managers are facilitators of ideas. This is as far as they normally go in the ‘idea’ space.
Business Requirements collection in classic project delivery requires extensive upfront documentation.
Agile project delivery analyzes requirements iteratively.
However, the project manager is a facilitator/planner first and foremost, therefore topic knowledge is not expected.
I mean business domain, not technical domain (to confuse matters, it is true that in some instances, it can be both technical and business domains that are important for a single individual to master).
Product managers are domain experts. They will become one if they are training/new.
They lead discovery.
Product Manager-led discovery is much more than requirements gathering.
Requirements gathering involves a Business Analyst interviewing people and documenting their requests.
The project manager calculates what fits and what doesn't using their Iron Triangle (presumably in their head) and reports back to Steering.
If this requirements-gathering exercise failed to identify requirements, what would a project manager do? or bewildered by project requirements and scope?
They would tell Steering they need a Business SME or Business Lead assigning or more of their time.
Product discovery requires the Product Manager's subject knowledge and a new mindset.
How should a Product Manager handle confusing requirements?
Product Managers handle these challenges with their talents and tools. They use their own knowledge to fill in ambiguity, but they have the discipline to validate those assumptions.
To define the problem, they may perform qualitative or quantitative primary research.
They might discuss with UX and Engineering on a whiteboard and test assumptions or hypotheses.
Do Product Managers escalate confusing requirements to Steering/Senior leaders? They would fix that themselves.
Product managers raise unclear strategy and outcomes to senior stakeholders. Open talks, soft skills, and data help them do this. They rarely raise requirements since they have their own means of handling them without top stakeholder participation.
Discovery is greenfield, exploratory, research-based, and needs higher-order stakeholder management, user research, and UX expertise.
Product Managers also aid discovery. They lead discovery. They will not leave customer/user engagement to a Business Analyst. Administratively, a business analyst could aid. In fact, many product organizations discourage business analysts (rely on PM, UX, and engineer involvement with end-users instead).
The Product Manager must drive user interaction, research, ideation, and problem analysis, therefore a Product professional must be skilled and confident.
Creating vs. receiving and having an entrepreneurial attitude

Product novices and project managers focus on details rather than the big picture. Project managers prefer spreadsheets to strategy whiteboards and vision statements.
These folks ask their manager or senior stakeholders, "What should we do?"
They then elaborate (in Jira, in XLS, in Confluence or whatever).
They want that plan populated fast because it reduces uncertainty about what's going on and who's supposed to do what.
Skilled Product Managers don't only ask folks Should we?
They're suggesting this, or worse, Senior stakeholders, here are some options. After asking and researching, they determine what value this product adds, what problems it solves, and what behavior it changes.
Therefore, to move into Product, you need to broaden your view and have courage in your ability to discover ideas, find insightful pieces of information, and collate them to form a valuable plan of action. You are constantly defining RoI and building Business Cases, so much so that you no longer create documents called Business Cases, it is simply ingrained in your work through metrics, intelligence, and insights.
Product Management is not a free lunch.
Plateless.
Plates and food must be prepared.
In conclusion, Product Managers must make at least three mentality shifts:
You put value first in all things. Time, money, and scope are not as important as knowing what is valuable.
You have faith in the field and have the ability to direct the search. YYou facilitate, but you don’t just facilitate. You wouldn't want to limit your domain expertise in that manner.
You develop concepts, strategies, and vision. You are not a waiter or an inbox where other people can post suggestions; you don't merely ask folks for opinion and record it. However, you excel at giving things that aren't clearly spoken or written down physical form.
Sam Hickmann
3 years ago
Improving collaboration with the Six Thinking Hats
Six Thinking Hats was written by Dr. Edward de Bono. "Six Thinking Hats" and parallel thinking allow groups to plan thinking processes in a detailed and cohesive way, improving collaboration.
Fundamental ideas
In order to develop strategies for thinking about specific issues, the method assumes that the human brain thinks in a variety of ways that can be intentionally challenged. De Bono identifies six brain-challenging directions. In each direction, the brain brings certain issues into conscious thought (e.g. gut instinct, pessimistic judgement, neutral facts). Some may find wearing hats unnatural, uncomfortable, or counterproductive.
The example of "mismatch" sensitivity is compelling. In the natural world, something out of the ordinary may be dangerous. This mode causes negative judgment and critical thinking.
Colored hats represent each direction. Putting on a colored hat symbolizes changing direction, either literally or metaphorically. De Bono first used this metaphor in his 1971 book "Lateral Thinking for Management" to describe a brainstorming framework. These metaphors allow more complete and elaborate thought separation. Six thinking hats indicate ideas' problems and solutions.
Similarly, his CoRT Thinking Programme introduced "The Five Stages of Thinking" method in 1973.
| HAT | OVERVIEW | TECHNIQUE |
|---|---|---|
| BLUE | "The Big Picture" & Managing | CAF (Consider All Factors); FIP (First Important Priorities) |
| WHITE | "Facts & Information" | Information |
| RED | "Feelings & Emotions" | Emotions and Ego |
| BLACK | "Negative" | PMI (Plus, Minus, Interesting); Evaluation |
| YELLOW | "Positive" | PMI |
| GREEN | "New Ideas" | Concept Challenge; Yes, No, Po |
Strategies and programs
After identifying the six thinking modes, programs can be created. These are groups of hats that encompass and structure the thinking process. Several of these are included in the materials for franchised six hats training, but they must often be adapted. Programs are often "emergent," meaning the group plans the first few hats and the facilitator decides what to do next.
The group agrees on how to think, then thinks, then evaluates the results and decides what to do next. Individuals or groups can use sequences (and indeed hats). Each hat is typically used for 2 minutes at a time, although an extended white hat session is common at the start of a process to get everyone on the same page. The red hat is recommended to be used for a very short period to get a visceral gut reaction – about 30 seconds, and in practice often takes the form of dot-voting.
| ACTIVITY | HAT SEQUENCE |
|---|---|
| Initial Ideas | Blue, White, Green, Blue |
| Choosing between alternatives | Blue, White, (Green), Yellow, Black, Red, Blue |
| Identifying Solutions | Blue, White, Black, Green, Blue |
| Quick Feedback | Blue, Black, Green, Blue |
| Strategic Planning | Blue, Yellow, Black, White, Blue, Green, Blue |
| Process Improvement | Blue, White, White (Other People's Views), Yellow, Black, Green, Red, Blue |
| Solving Problems | Blue, White, Green, Red, Yellow, Black, Green, Blue |
| Performance Review | Blue, Red, White, Yellow, Black, Green, Blue |
Use
Speedo's swimsuit designers reportedly used the six thinking hats. "They used the "Six Thinking Hats" method to brainstorm, with a green hat for creative ideas and a black one for feasibility.
Typically, a project begins with extensive white hat research. Each hat is used for a few minutes at a time, except the red hat, which is limited to 30 seconds to ensure an instinctive gut reaction, not judgement. According to Malcolm Gladwell's "blink" theory, this pace improves thinking.
De Bono believed that the key to a successful Six Thinking Hats session was focusing the discussion on a particular approach. A meeting may be called to review and solve a problem. The Six Thinking Hats method can be used in sequence to explore the problem, develop a set of solutions, and choose a solution through critical examination.
Everyone may don the Blue hat to discuss the meeting's goals and objectives. The discussion may then shift to Red hat thinking to gather opinions and reactions. This phase may also be used to determine who will be affected by the problem and/or solutions. The discussion may then shift to the (Yellow then) Green hat to generate solutions and ideas. The discussion may move from White hat thinking to Black hat thinking to develop solution set criticisms.
Because everyone is focused on one approach at a time, the group is more collaborative than if one person is reacting emotionally (Red hat), another is trying to be objective (White hat), and another is critical of the points which emerge from the discussion (Black hat). The hats help people approach problems from different angles and highlight problem-solving flaws.
Jason Kottke
3 years ago
Lessons on Leadership from the Dancing Guy
This is arguably the best three-minute demonstration I've ever seen of anything. Derek Sivers turns a shaky video of a lone dancing guy at a music festival into a leadership lesson.
A leader must have the courage to stand alone and appear silly. But what he's doing is so straightforward that it's almost instructive. This is critical. You must be simple to follow!
Now comes the first follower, who plays an important role: he publicly demonstrates how to follow. The leader embraces him as an equal, so it's no longer about the leader — it's about them, plural. He's inviting his friends to join him. It takes courage to be the first follower! You stand out and dare to be mocked. Being a first follower is a style of leadership that is underappreciated. The first follower elevates a lone nut to the position of leader. If the first follower is the spark that starts the fire, the leader is the flint.
This link was sent to me by @ottmark, who noted its resemblance to Kurt Vonnegut's three categories of specialists required for revolution.
The rarest of these specialists, he claims, is an actual genius – a person capable generating seemingly wonderful ideas that are not widely known. "A genius working alone is generally dismissed as a crazy," he claims.
The second type of specialist is much easier to find: a highly intellectual person in good standing in his or her community who understands and admires the genius's new ideas and can attest that the genius is not insane. "A person like him working alone can only crave loudly for changes, but fail to say what their shapes should be," Slazinger argues.
Jeff Veen reduced the three personalities to "the inventor, the investor, and the evangelist" on Twitter.
You might also like

Rita McGrath
3 years ago
Flywheels and Funnels
Traditional sales organizations used the concept of a sales “funnel” to describe the process through which potential customers move, ending up with sales at the end. Winners today have abandoned that way of thinking in favor of building flywheels — business models in which every element reinforces every other.
Ah, the marketing funnel…
Prospective clients go through a predictable set of experiences, students learn in business school marketing classes. It looks like this:

Understanding the funnel helps evaluate sales success indicators. Gail Goodwin, former CEO of small business direct mail provider Constant Contact, said managing the pipeline was key to escaping the sluggish SaaS ramp of death.
Like the funnel concept. To predict how well your business will do, measure how many potential clients are aware of it (awareness) and how many take the next step. If 1,000 people heard about your offering and 10% showed interest, you'd have 100 at that point. If 50% of these people made buyer-like noises, you'd know how many were, etc. It helped model buying trends.
TV, magazine, and radio advertising are pricey for B2C enterprises. Traditional B2B marketing involved armies of sales reps, which was expensive and a barrier to entry.
Cracks in the funnel model
Digital has exposed the funnel's limitations. Hubspot was born at a time when buyers and sellers had huge knowledge asymmetries, according to co-founder Brian Halligan. Those selling a product could use the buyer's lack of information to become a trusted partner.
As the world went digital, getting information and comparing offerings became faster, easier, and cheaper. Buyers didn't need a seller to move through a funnel. Interactions replaced transactions, and the relationship didn't end with a sale.
Instead, buyers and sellers interacted in a constant flow. In many modern models, the sale is midway through the process (particularly true with subscription and software-as-a-service models). Example:
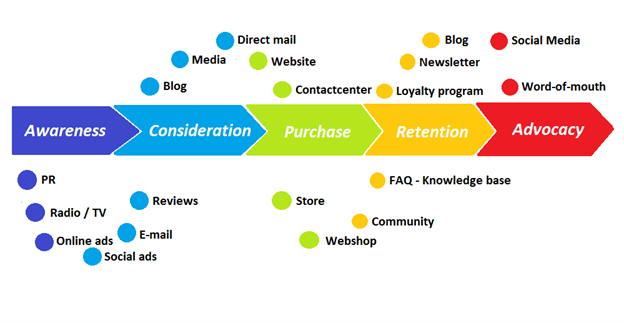
You're creating a winding journey with many touch points, not a funnel (and lots of opportunities for customers to get lost).
From winding journey to flywheel
Beyond this revised view of an interactive customer journey, a company can create what Jim Collins famously called a flywheel. Imagine rolling a heavy disc on its axis. The first few times you roll it, you put in a lot of effort for a small response. The same effort yields faster turns as it gains speed. Over time, the flywheel gains momentum and turns without your help.
Modern digital organizations have created flywheel business models, in which any additional force multiplies throughout the business. The flywheel becomes a force multiplier, according to Collins.
Amazon is a famous flywheel example. Collins explained the concept to Amazon CEO Jeff Bezos at a corporate retreat in 2001. In The Everything Store, Brad Stone describes in his book The Everything Store how he immediately understood Amazon's levers.
The result (drawn on a napkin):
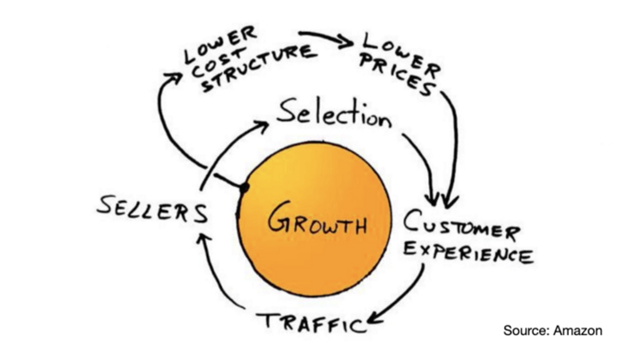
Low prices and a large selection of products attracted customers, while a focus on customer service kept them coming back, increasing traffic. Third-party sellers then increased selection. Low-cost structure supports low-price commitment. It's brilliant! Every wheel turn creates acceleration.
Where from here?
Flywheel over sales funnel! Consider these business terms.

Stephen Moore
3 years ago
Web 2 + Web 3 = Web 5.
Monkey jpegs and shitcoins have tarnished Web3's reputation. Let’s move on.

Web3 was called "the internet's future."
Well, 'crypto bros' shouted about it loudly.
As quickly as it arrived to be the next internet, it appears to be dead. It's had scandals, turbulence, and crashes galore:
Web 3.0's cryptocurrencies have crashed. Bitcoin's all-time high was $66,935. This month, Ethereum fell from $2130 to $1117. Six months ago, the cryptocurrency market peaked at $3 trillion. Worst is likely ahead.
Gas fees make even the simplest Web3 blockchain transactions unsustainable.
Terra, Luna, and other dollar pegs collapsed, hurting crypto markets. Celsius, a crypto lender backed by VCs and Canada's second-largest pension fund, and Binance, a crypto marketplace, have withheld money and coins. They're near collapse.
NFT sales are falling rapidly and losing public interest.
Web3 has few real-world uses, like most crypto/blockchain technologies. Web3's image has been tarnished by monkey profile pictures and shitcoins while failing to become decentralized (the whole concept is controlled by VCs).
The damage seems irreparable, leaving Web3 in the gutter.
Step forward our new saviour — Web5
Fear not though, as hero awaits to drag us out of the Web3 hellscape. Jack Dorsey revealed his plan to save the internet quickly.
Dorsey has long criticized Web3, believing that VC capital and silicon valley insiders have created a centralized platform. In a tweet that upset believers and VCs (he was promptly blocked by Marc Andreessen), Dorsey argued, "You don't own "Web3." VCs and LPs do. Their incentives prevent it. It's a centralized organization with a new name.
Dorsey announced Web5 on June 10 in a very Elon-like manner. Block's TBD unit will work on the project (formerly Square).
Web5's pitch is that users will control their own data and identity. Bitcoin-based. Sound familiar? The presentation pack's official definition emphasizes decentralization. Web5 is a decentralized web platform that enables developers to write decentralized web apps using decentralized identifiers, verifiable credentials, and decentralized web nodes, returning ownership and control over identity and data to individuals.
Web5 would be permission-less, open, and token-less. What that means for Earth is anyone's guess. Identity. Ownership. Blockchains. Bitcoin. Different.
Web4 appears to have been skipped, forever destined to wish it could have shown the world what it could have been. (It was probably crap.) As this iteration combines Web2 and Web3, simple math and common sense add up to 5. Or something.
Dorsey and his team have had this idea simmering for a while. Daniel Buchner, a member of Block's Decentralized Identity team, said, "We're finishing up Web5's technical components."
Web5 could be the project that decentralizes the internet. It must be useful to users and convince everyone to drop the countless Web3 projects, products, services, coins, blockchains, and websites being developed as I write this.
Web5 may be too late for Dorsey and the incoming flood of creators.
Web6 is planned!
The next months and years will be hectic and less stable than the transition from Web 1.0 to Web 2.0.
Web1 was around 1991-2004.
Web2 ran from 2004 to 2021. (though the Web3 term was first used in 2014, it only really gained traction years later.)
Web3 lasted a year.
Web4 is dead.
Silicon Valley billionaires are turning it into a startup-style race, each disrupting the next iteration until they crack it. Or destroy it completely.
Web5 won't last either.

Web3Lunch
3 years ago
An employee of OpenSea might get a 40-year prison sentence for insider trading using NFTs.

The space had better days. Those greenish spikes...oh wow, haven't felt that in ages. Cryptocurrencies and NFTs have lost popularity. Google agrees. Both are declining.
As seen below, crypto interest spiked in May because of the Luna fall. NFT interest is similar to early October last year.
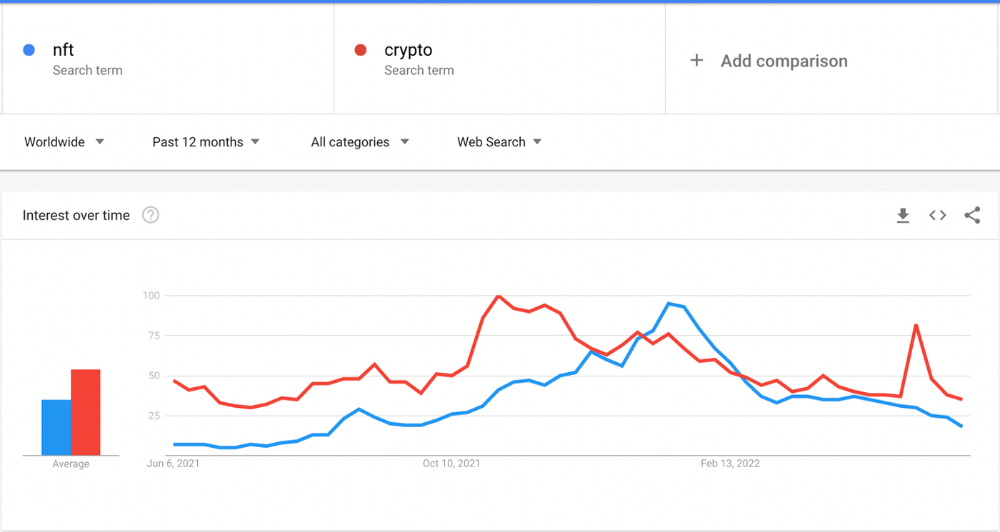
This makes me think NFTs are mostly hype and FOMO. No art or community. I've seen enough initiatives to know that communities stick around if they're profitable. Once it starts falling, they move on to the next project. The space has no long-term investments. Flip everything.
OpenSea trading volume has stayed steady for months. May's volume is 1.8 million ETH ($3.3 billion).
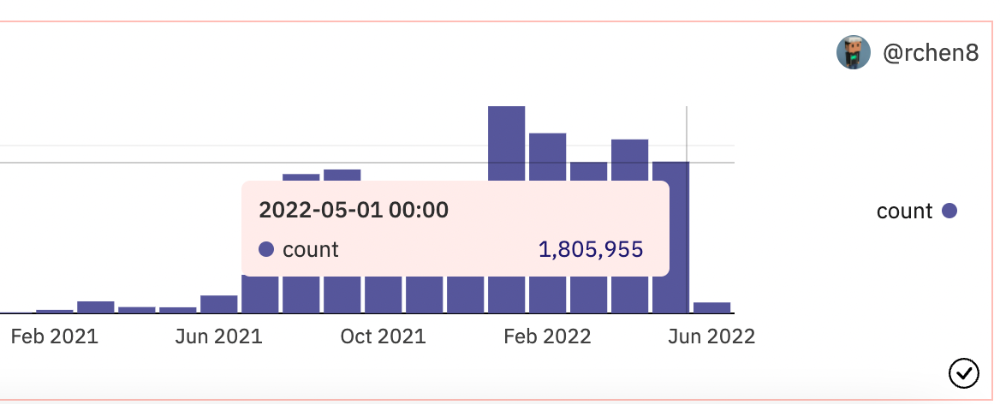
Despite this, I think NFTs and crypto will stick around. In bad markets, builders gain most.
Only 4k developers are active on Ethereum blockchain. It's low. A great chance for the space enthusiasts.
An employee of OpenSea might get a 40-year prison sentence for insider trading using NFTs.
Nathaniel Chastian, an OpenSea employee, traded on insider knowledge. He'll serve 40 years for that.
Here's what happened if you're unfamiliar.
OpenSea is a secondary NFT marketplace. Their homepage featured remarkable drops. Whatever gets featured there, NFT prices will rise 5x.
Chastian was at OpenSea. He chose forthcoming NFTs for OpenSeas' webpage.
Using anonymous digital currency wallets and OpenSea accounts, he would buy NFTs before promoting them on the homepage, showcase them, and then sell them for at least 25 times the price he paid.
From June through September 2021, this happened. Later caught, fired. He's charged with wire fraud and money laundering, each carrying a 20-year maximum penalty.
Although web3 space is all about decentralization, a step like this is welcomed since it restores faith in the area. We hope to see more similar examples soon.
Here's the press release.

Understanding smart contracts
@cantino.eth has a Twitter thread on smart contracts. Must-read. Also, he appears educated about the space, so follow him.

