More on Entrepreneurship/Creators

Aaron Dinin, PhD
3 years ago
I put my faith in a billionaire, and he destroyed my business.
How did his money blind me?

Like most fledgling entrepreneurs, I wanted a mentor. I met as many nearby folks with "entrepreneur" in their LinkedIn biographies for coffee.
These meetings taught me a lot, and I'd suggest them to any new creator. Attention! Meeting with many experienced entrepreneurs means getting contradictory advice. One entrepreneur will tell you to do X, then the next one you talk to may tell you to do Y, which are sometimes opposites. You'll have to chose which suggestion to take after the chats.
I experienced this. Same afternoon, I had two coffee meetings with experienced entrepreneurs. The first meeting was with a billionaire entrepreneur who took his company public.
I met him in a swanky hotel lobby and ordered a drink I didn't pay for. As a fledgling entrepreneur, money was scarce.
During the meeting, I demoed the software I'd built, he liked it, and we spent the hour discussing what features would make it a success. By the end of the meeting, he requested I include a killer feature we both agreed would attract buyers. The feature was complex and would require some time. The billionaire I was sipping coffee with in a beautiful hotel lobby insisted people would love it, and that got me enthusiastic.
The second meeting was with a young entrepreneur who had recently raised a small amount of investment and looked as eager to pitch me as I was to pitch him. I forgot his name. I mostly recall meeting him in a filthy coffee shop in a bad section of town and buying his pricey cappuccino. Water for me.
After his pitch, I demoed my app. When I was done, he barely noticed. He questioned my customer acquisition plan. Who was my client? What did they offer? What was my plan? Etc. No decent answers.
After our meeting, he insisted I spend more time learning my market and selling. He ignored my questions about features. Don't worry about features, he said. Customers will request features. First, find them.
Putting your faith in results over relevance
Problems plagued my afternoon. I met with two entrepreneurs who gave me differing advice about how to proceed, and I had to decide which to pursue. I couldn't decide.
Ultimately, I followed the advice of the billionaire.
Obviously.
Who wouldn’t? That was the guy who clearly knew more.
A few months later, I constructed the feature the billionaire said people would line up for.
The new feature was unpopular. I couldn't even get the billionaire to answer an email showing him what I'd done. He disappeared.
Within a few months, I shut down the company, wasting all the time and effort I'd invested into constructing the killer feature the billionaire said I required.
Would follow the struggling entrepreneur's advice have saved my company? It would have saved me time in retrospect. Potential consumers would have told me they didn't want what I was producing, and I could have shut down the company sooner or built something they did want. Both outcomes would have been better.
Now I know, but not then. I favored achievement above relevance.
Success vs. relevance
The millionaire gave me advice on building a large, successful public firm. A successful public firm is different from a startup. Priorities change in the last phase of business building, which few entrepreneurs reach. He gave wonderful advice to founders trying to double their stock values in two years, but it wasn't beneficial for me.
The other failing entrepreneur had relevant, recent experience. He'd recently been in my shoes. We still had lots of problems. He may not have achieved huge success, but he had valuable advice on how to pass the closest hurdle.
The money blinded me at the moment. Not alone So much of company success is defined by money valuations, fundraising, exits, etc., so entrepreneurs easily fall into this trap. Money chatter obscures the value of knowledge.
Don't base startup advice on a person's income. Focus on what and when the person has learned. Relevance to you and your goals is more important than a person's accomplishments when considering advice.

Nick Nolan
3 years ago
How to Make $1,037,100 in 4 Months with This Weird Website
One great idea might make you rich.

Imagine having a million-dollar concept in college that made a million.
2005 precisely.
Alex Tew, 21, from Wiltshire, England, created The Million Dollar Homepage in August 2005. The idea is basic but beyond the ordinary, which is why it worked.
Alex built a 1,000,000-pixel webpage.
Each website pixel would cost $1. Since pixels are hard to discern, he sold 10x10 squares for $100.
He'd make a million if all the spots sold.
He may have thought about NFTs and the Metaverse decades ago.
MillionDollarHomepage.com launched in 2005.
Businesses and individuals could buy a website spot and add their logo, website link, and tagline. You bought an ad, but nobody visited the website.
If a few thousand people visited the website, it could drive traffic to your business's site.
Alex promised buyers the website would be up for 5 years, so it was a safe bet.
Alex's friend with a music website was the first to buy real estate on the site. Within two weeks, 4,700 pixels sold, and a tracker showed how many were sold and available.

Word-of-mouth marketing got the press's attention quickly. Everyone loves reading about new ways to make money, so it was a good news story.
By September, over 250,000 pixels had been sold, according to a BBC press release.
Alex and the website gained more media and public attention, so traffic skyrocketed. Two months after the site launched, 1,400 customers bought more than 500,000 pixels.
Businesses bought online real estate. They heard thousands visited the site, so they could get attention cheaply.
Unless you bought a few squares, I'm not sure how many people would notice your ad or click your link.
A sponge website owner emailed Alex:
“We tried Million Dollar Homepage because we were impressed at the level of ingenuity and the sheer simplicity of it. If we’re honest, we didn’t expect too much from it. Now, as a direct result, we are pitching for £18,000 GBP worth of new clients and have seen our site traffic increase over a hundred-fold. We’re even going to have to upgrade our hosting facility! It’s been exceptional.”
Web.archive.org screenshots show how the website changed.
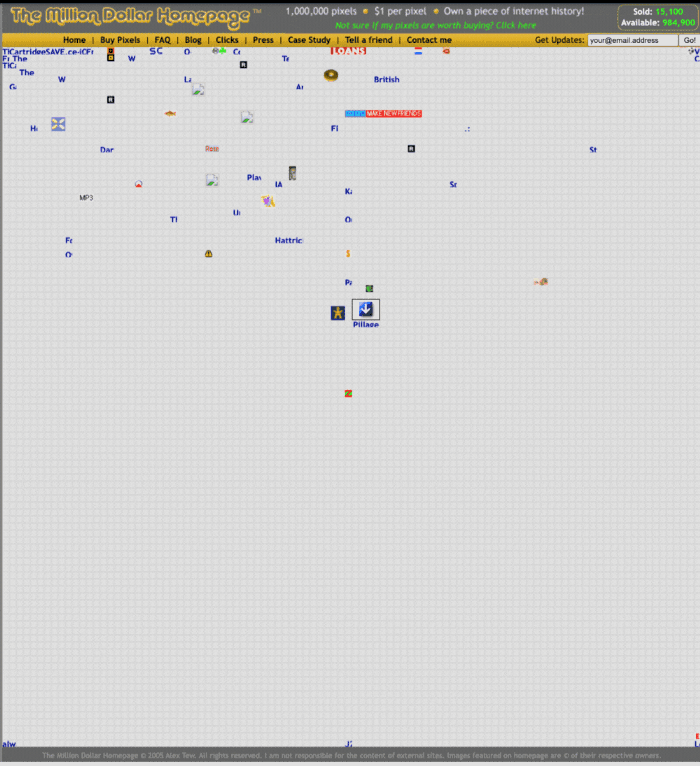
“The idea is to create something of an internet time capsule: a homepage that is unique and permanent. Everything on the internet keeps changing so fast, it will be nice to have something that stays solid and permanent for many years. You can be a part of that!” Alex Tew, 2005
The last 1,000 pixels were sold on January 1, 2006.
By then, the homepage had hundreds of thousands of monthly visitors. Alex put the last space on eBay due to high demand.
MillionDollarWeightLoss.com won the last pixels for $38,100, bringing revenue to $1,037,100 in 4 months.

Many have tried to replicate this website's success. They've all failed.
This idea only worked because no one had seen this website before.
This winner won't be repeated, but it should inspire you to try something new and creative.
Still popular, you could buy one of the linked domains. You can't buy pixels, but you can buy an expired domain.
One link I clicked costs $59,888.

You'd own a piece of internet history if you spent that much on a domain.
Someone bought stablesgallery.co.uk after the domain expired and restored it.
Many of the linked websites have expired or been redirected, but some still link to the original. I couldn't find sponge's website. Can you?
This is a great example of how a simple creative idea can go viral.
Comment on this amazing success story.

Mangu Solutions
3 years ago
Growing a New App to $15K/mo in 6 Months [SaaS Case Study]
Discover How We Used Facebook Ads to Grow a New Mobile App from $0 to $15K MRR in Just 6 Months and Our Strategy to Hit $100K a Month.
Our client introduced a mobile app for Poshmark resellers in December and wanted as many to experience it and subscribe to the monthly plan.
An Error We Committed
We initiated a Facebook ad campaign with a "awareness" goal, not "installs." This sent them to a landing page that linked to the iPhone App Store and Android Play Store. Smart, right?
We got some installs, but we couldn't tell how many came from the ad versus organic/other channels because the objective we chose only reported landing page clicks, not app installs.
We didn't know which interest groups/audiences had the best cost per install (CPI) to optimize and scale our budget.
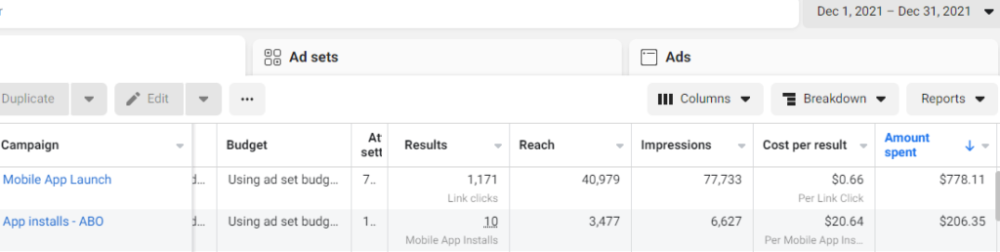
After spending $700 without adequate data (installs and trials report), we stopped the campaign and worked with our client's app developer to set up app events tracking.
This allowed us to create an installs campaign and track installs, trials, and purchases (in some cases).
Finding a Successful Audience
Once we knew what ad sets brought in what installs at what cost, we began optimizing and testing other interest groups and audiences, growing the profitable low CPI ones and eliminating the high CPI ones.
We did all our audience testing using an ABO campaign (Ad Set Budget Optimization), spending $10 to $30 on each ad set for three days and optimizing afterward. All ad sets under $30 were moved to a CBO campaign (Campaign Budget Optimization).
We let Facebook's AI decide how much to spend on each ad set, usually the one most likely to convert at the lowest cost.
If the CBO campaign maintains a nice CPI, we keep increasing the budget by $50 every few days or duplicating it sometimes in order to double the budget. This is how we've scaled to $400/day profitably.

Finding Successful Creatives
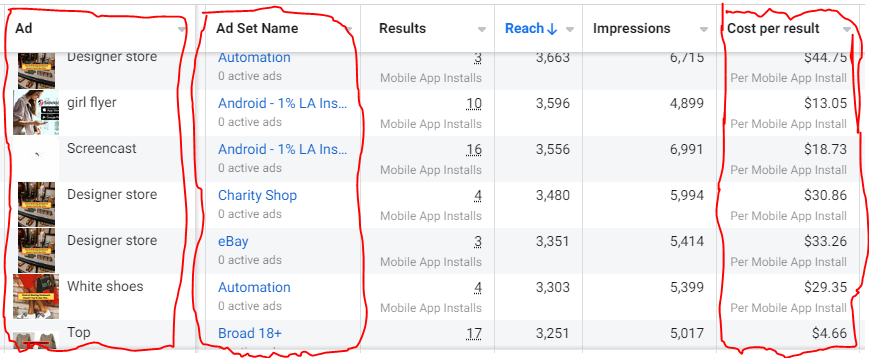
Per campaign, we tested 2-6 images/videos. Same ad copy and CTA. There was no clear winner because some images did better with some interest groups.
The image above with mail packages, for example, got us a cheap CPI of $9.71 from our Goodwill Stores interest group but, a high $48 CPI from our lookalike audience. Once we had statistically significant data, we turned off the high-cost ad.
New marketers who are just discovering A/B testing may assume it's black and white — winner and loser. However, Facebook ads' machine learning and reporting has gotten so sophisticated that it's hard to call a creative a flat-out loser, but rather a 'bad fit' for some audiences, and perfect for others.
You can see how each creative performs across age groups and optimize.
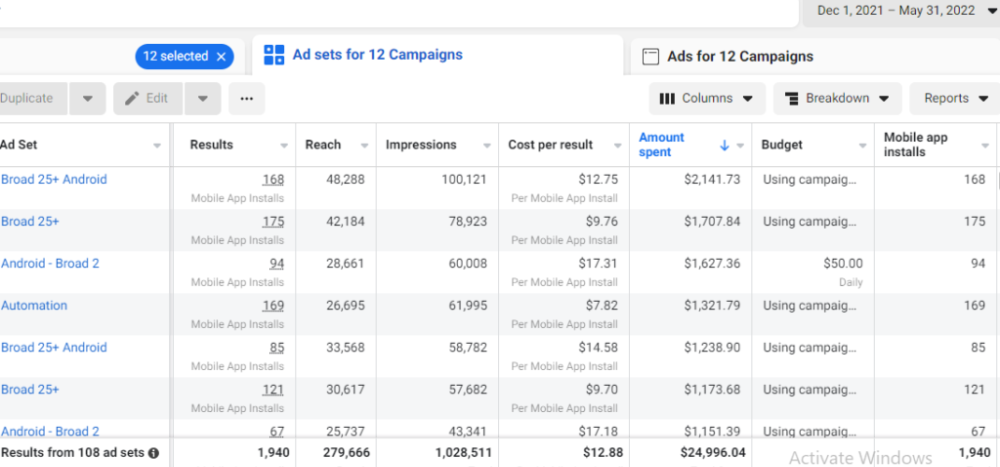
How Many Installs Did It Take Us to Earn $15K Per Month?
Six months after paying $25K, we got 1,940 app installs, 681 free trials, and 522 $30 monthly subscriptions. 522 * $30 gives us $15,660 in monthly recurring revenue (MRR).
Next, what? $100K per month
The conversation above is with the app's owner. We got on a 30-minute call where I shared how I plan to get the app to be making $100K a month like I’ve done for other businesses.
Reverse Engineering $100K
Formula:
For $100K/month, we need 3,334 people to pay $30/month. 522 people pay that. We need 2,812 more paid users.
522 paid users from 1,940 installs is a 27% conversion rate. To hit $100K/month, we need 10,415 more installs. Assuming...
With a $400 daily ad spend, we average 40 installs per day. This means that if everything stays the same, it would take us 260 days (around 9 months) to get to $100K a month (MRR).
Conclusion
You must market your goods to reach your income objective (without waiting forever). Paid ads is the way to go if you hate knocking on doors or irritating friends and family (who aren’t scalable anyways).
You must also test and optimize different angles, audiences, interest groups, and creatives.
You might also like

Mike Meyer
3 years ago
Reality Distortion
Old power paradigm blocks new planetary paradigm

The difference between our reality and the media's reality is like a tale of two worlds. The greatest and worst of times, really.
Expanding information demands complex skills and understanding to separate important information from ignorance and crap. And that's just the start of determining the source's aim.
Trust who? We see people trust liars in public and then be destroyed by their decisions. Mistakes may be devastating.
Many give up and don't trust anyone. Reality is a choice, though. Same risks.
We must separate our needs and wants from reality. Needs and wants have rules. Greed and selfishness create an unlivable planet.
Culturally, we know this, but we ignore it as foolish. Selfish and greedy people obtain what they want, while others suffer.
We invade, plunder, rape, and burn. We establish civilizations by institutionalizing an exploitable underclass and denying its existence. These cultural lies promote greed and selfishness despite their destructiveness.
Controlling parts of society institutionalize these lies as fact. Many of each age are willing to gamble on greed because they were taught to see greed and selfishness as principles justified by prosperity.
Our cultural understanding recognizes the long-term benefits of collaboration and sharing. This older understanding generates an increasing tension between greedy people and those who see its planetary effects.
Survival requires distinguishing between global and regional realities. Simple, yet many can't do it. This is the first time human greed has had a global impact.
In the past, conflict stories focused on regional winners and losers. Losers lose, winners win, etc. Powerful people see potential decades of nuclear devastation as local, overblown, and not personally dangerous.
Mutually Assured Destruction (MAD) was a human choice that required people to acquiesce to irrational devastation. This prevented nuclear destruction. Most would refuse.
A dangerous “solution” relies on nuclear trigger-pullers not acting irrationally. Since then, we've collected case studies of sane people performing crazy things in experiments. We've been lucky, but the climate apocalypse could be different.
Climate disaster requires only continuing current behavior. These actions already cause global harm, but that's not a threat. These activities must be viewed differently.
Once grasped, denying planetary facts is hard to accept. Deniers can't think beyond regional power. Seeing planet-scale is unusual.
Decades of indoctrination defining any planetary perspective as un-American implies communal planetary assets are for plundering. The old paradigm limits any other view.
In the same way, the new paradigm sees the old regional power paradigm as a threat to planetary civilization and lifeforms. Insane!
While MAD relied on leaders not acting stupidly to trigger a nuclear holocaust, the delayed climatic holocaust needs correcting centuries of lunacy. We must stop allowing craziness in global leadership.
Nothing in our acknowledged past provides a paradigm for such. Only primitive people have failed to reach our level of sophistication.
Before European colonization, certain North American cultures built sophisticated regional nations but abandoned them owing to authoritarian cruelty and destruction. They were overrun by societies that saw no wrong in perpetual exploitation. David Graeber's The Dawn of Everything is an example of historical rediscovery, which is now crucial.
From the new paradigm's perspective, the old paradigm is irrational, yet it's too easy to see those in it as ignorant or malicious, if not both. These people are both, but the collapsing paradigm they promote is older or more ingrained than we think.
We can't shift that paradigm's view of a dead world. We must eliminate this mindset from our nations' leadership. No other way will preserve the earth.
Change is occurring. As always with tremendous transition, younger people are building the new paradigm.
The old paradigm's disintegration is insane. The ability to detect errors and abandon their sources is more important than age. This is gaining recognition.
The breakdown of the previous paradigm is not due to senile leadership, but to systemic problems that the current, conservative leadership cannot recognize.
Stop following the old paradigm.

Duane Michael
3 years ago
Don't Fall Behind: 7 Subjects You Must Understand to Keep Up with Technology
As technology develops, you should stay up to date

You don't want to fall behind, do you? This post covers 7 tech-related things you should know.
You'll learn how to operate your computer (and other electronic devices) like an expert and how to leverage the Internet and social media to create your brand and business. Read on to stay relevant in today's tech-driven environment.
You must learn how to code.
Future-language is coding. It's how we and computers talk. Learn coding to keep ahead.
Try Codecademy or Code School. There are also numerous free courses like Coursera or Udacity, but they take a long time and aren't necessarily self-paced, so it can be challenging to find the time.
Artificial intelligence (AI) will transform all jobs.
Our skillsets must adapt with technology. AI is a must-know topic. AI will revolutionize every employment due to advances in machine learning.
Here are seven AI subjects you must know.
What is artificial intelligence?
How does artificial intelligence work?
What are some examples of AI applications?
How can I use artificial intelligence in my day-to-day life?
What jobs have a high chance of being replaced by artificial intelligence and how can I prepare for this?
Can machines replace humans? What would happen if they did?
How can we manage the social impact of artificial intelligence and automation on human society and individual people?
Blockchain Is Changing the Future
Few of us know how Bitcoin and blockchain technology function or what impact they will have on our lives. Blockchain offers safe, transparent, tamper-proof transactions.
It may alter everything from business to voting. Seven must-know blockchain topics:
Describe blockchain.
How does the blockchain function?
What advantages does blockchain offer?
What possible uses for blockchain are there?
What are the dangers of blockchain technology?
What are my options for using blockchain technology?
What does blockchain technology's future hold?
Cryptocurrencies are here to stay
Cryptocurrencies employ cryptography to safeguard transactions and manage unit creation. Decentralized cryptocurrencies aren't controlled by governments or financial institutions.

Bitcoin, the first cryptocurrency, was launched in 2009. Cryptocurrencies can be bought and sold on decentralized exchanges.
Bitcoin is here to stay.
Bitcoin isn't a fad, despite what some say. Since 2009, Bitcoin's popularity has grown. Bitcoin is worth learning about now. Since 2009, Bitcoin has developed steadily.
With other cryptocurrencies emerging, many people are wondering if Bitcoin still has a bright future. Curiosity is natural. Millions of individuals hope their Bitcoin investments will pay off since they're popular now.
Thankfully, they will. Bitcoin is still running strong a decade after its birth. Here's why.
The Internet of Things (IoT) is no longer just a trendy term.
IoT consists of internet-connected physical items. These items can share data. IoT is young but developing fast.
20 billion IoT-connected devices are expected by 2023. So much data! All IT teams must keep up with quickly expanding technologies. Four must-know IoT topics:
Recognize the fundamentals: Priorities first! Before diving into more technical lingo, you should have a fundamental understanding of what an IoT system is. Before exploring how something works, it's crucial to understand what you're working with.
Recognize Security: Security does not stand still, even as technology advances at a dizzying pace. As IT professionals, it is our duty to be aware of the ways in which our systems are susceptible to intrusion and to ensure that the necessary precautions are taken to protect them.
Be able to discuss cloud computing: The cloud has seen various modifications over the past several years once again. The use of cloud computing is also continually changing. Knowing what kind of cloud computing your firm or clients utilize will enable you to make the appropriate recommendations.
Bring Your Own Device (BYOD)/Mobile Device Management (MDM) is a topic worth discussing (MDM). The ability of BYOD and MDM rules to lower expenses while boosting productivity among employees who use these services responsibly is a major factor in their continued growth in popularity.
IoT Security is key
As more gadgets connect, they must be secure. IoT security includes securing devices and encrypting data. Seven IoT security must-knows:
fundamental security ideas
Authorization and identification
Cryptography
electronic certificates
electronic signatures
Private key encryption
Public key encryption
Final Thoughts
With so much going on in the globe, it can be hard to stay up with technology. We've produced a list of seven tech must-knows.

Jake Prins
3 years ago
What are NFTs 2.0 and what issues are they meant to address?
New standards help NFTs reach their full potential.

NFTs lack interoperability and functionality. They have great potential but are mostly speculative. To maximize NFTs, we need flexible smart contracts.
Current requirements are too restrictive.
Most NFTs are based on ERC-721, which makes exchanging them easy. CryptoKitties, a popular online game, used the 2017 standard to demonstrate NFTs' potential.
This simple standard includes a base URI and incremental IDs for tokens. Add the tokenID to the base URI to get the token's metadata.
This let creators collect NFTs. Many NFT projects store metadata on IPFS, a distributed storage network, but others use Google Drive. NFT buyers often don't realize that if the creators delete or move the files, their NFT is just a pointer.
This isn't the standard's biggest issue. There's no way to validate NFT projects.
Creators are one of the most important aspects of art, but nothing is stored on-chain.
ERC-721 contracts only have a name and symbol.
Most of the data on OpenSea's collection pages isn't from the NFT's smart contract. It was added through a platform input field, so it's in the marketplace's database. Other websites may have different NFT information.
In five years, your NFT will be just a name, symbol, and ID.
Your NFT doesn't mention its creators. Although the smart contract has a public key, it doesn't reveal who created it.
The NFT's creators and their reputation are crucial to its value. Think digital fashion and big brands working with well-known designers when more professionals use NFTs. Don't you want them in your NFT?
Would paintings be as valuable if their artists were unknown? Would you believe it's real?
Buying directly from an on-chain artist would reduce scams. Current standards don't allow this data.
Most creator profiles live on centralized marketplaces and could disappear. Current platforms have outpaced underlying standards. The industry's standards are lagging.
For NFTs to grow beyond pointers to a monkey picture file, we may need to use new Web3-based standards.
Introducing NFTs 2.0
Fabian Vogelsteller, creator of ERC-20, developed new web3 standards. He proposed LSP7 Digital Asset and LSP8 Identifiable Digital Asset, also called NFT 2.0.
NFT and token metadata inputs are extendable. Changes to on-chain metadata inputs allow NFTs to evolve. Instead of public keys, the contract can have Universal Profile addresses attached. These profiles show creators' faces and reputations. NFTs can notify asset receivers, automating smart contracts.
LSP7 and LSP8 use ERC725Y. Using a generic data key-value store gives contracts much-needed features:
The asset can be customized and made to stand out more by allowing for unlimited data attachment.
Recognizing changes to the metadata
using a hash reference for metadata rather than a URL reference
This base will allow more metadata customization and upgradeability. These guidelines are:
Genuine and Verifiable Now, the creation of an NFT by a specific Universal Profile can be confirmed by smart contracts.
Dynamic NFTs can update Flexible & Updatable Metadata, allowing certain things to evolve over time.
Protected metadata Now, secure metadata that is readable by smart contracts can be added indefinitely.
Better NFTS prevent the locking of NFTs by only being sent to Universal Profiles or a smart contract that can interact with them.
Summary
NFTS standards lack standardization and powering features, limiting the industry.
ERC-721 is the most popular NFT standard, but it only represents incremental tokenIDs without metadata or asset representation. No standard sender-receiver interaction or security measures ensure safe asset transfers.
NFT 2.0 refers to the new LSP7-DigitalAsset and LSP8-IdentifiableDigitalAsset standards.
They have new standards for flexible metadata, secure transfers, asset representation, and interactive transfer.
With NFTs 2.0 and Universal Profiles, creators could build on-chain reputations.
NFTs 2.0 could bring the industry's needed innovation if it wants to move beyond trading profile pictures for speculation.
