More on Web3 & Crypto

Robert Kim
4 years ago
Crypto Legislation Might Progress Beyond Talk in 2022
Financial regulators have for years attempted to apply existing laws to the multitude of issues created by digital assets. In 2021, leading federal regulators and members of Congress have begun to call for legislation to address these issues. As a result, 2022 may be the year when federal legislation finally addresses digital asset issues that have been growing since the mining of the first Bitcoin block in 2009.
Digital Asset Regulation in the Absence of Legislation
So far, Congress has left the task of addressing issues created by digital assets to regulatory agencies. Although a Congressional Blockchain Caucus formed in 2016, House and Senate members introduced few bills addressing digital assets until 2018. As of October 2021, Congress has not amended federal laws on financial regulation, which were last significantly revised by the Dodd-Frank Act in 2010, to address digital asset issues.
In the absence of legislation, issues that do not fit well into existing statutes have created problems. An example is the legal status of digital assets, which can be considered to be either securities or commodities, and can even shift from one to the other over time. Years after the SEC’s 2017 report applying the definition of a security to digital tokens, the SEC and the CFTC have yet to clarify the distinction between securities and commodities for the thousands of digital assets in existence.
SEC Chair Gary Gensler has called for Congress to act, stating in August, “We need additional Congressional authorities to prevent transactions, products, and platforms from falling between regulatory cracks.” Gensler has reached out to Sen. Elizabeth Warren (D-Ma.), who has expressed her own concerns about the need for legislation.
Legislation on Digital Assets in 2021
While regulators and members of Congress talked about the need for legislation, and the debate over cryptocurrency tax reporting in the 2021 infrastructure bill generated headlines, House and Senate bills proposing specific solutions to various issues quietly started to emerge.
Digital Token Sales
Several House bills attempt to address securities law barriers to digital token sales—some of them by building on ideas proposed by regulators in past years.
Exclusion from the definition of a security. Congressional Blockchain Caucus members have been introducing bills to exclude digital tokens from the definition of a security since 2018, and they have revived those bills in 2021. They include the Token Taxonomy Act of 2021 (H.R. 1628), successor to identically named bills in 2018 and 2019, and the Securities Clarity Act (H.R. 4451), successor to a 2020 namesake.
Safe harbor. SEC Commissioner Hester Peirce proposed a regulatory safe harbor for token sales in 2020, and two 2021 bills have proposed statutory safe harbors. Rep. Patrick McHenry (R-N.C.), Republican leader of the House Financial Services Committee, introduced a Clarity for Digital Tokens Act of 2021 (H.R. 5496) that would amend the Securities Act to create a safe harbor providing a grace period of exemption from Securities Act registration requirements. The Digital Asset Market Structure and Investor Protection Act (H.R. 4741) from Rep. Don Beyer (D-Va.) would amend the Securities Exchange Act to define a new type of security—a “digital asset security”—and add issuers of digital asset securities to an existing provision for delayed registration of securities.
Stablecoins
Stablecoins—digital currencies linked to the value of the U.S. dollar or other fiat currencies—have not yet been the subject of regulatory action, although Treasury Secretary Janet Yellen and Federal Reserve Chair Jerome Powell have each underscored the need to create a regulatory framework for them. The Beyer bill proposes to create a regulatory regime for stablecoins by amending Title 31 of the U.S. Code. Treasury Department approval would be required for any “digital asset fiat-based stablecoin” to be issued or used, under an application process to be established by Treasury in consultation with the Federal Reserve, the SEC, and the CFTC.
Serious consideration for any of these proposals in the current session of Congress may be unlikely. A spate of autumn bills on crypto ransom payments (S. 2666, S. 2923, S. 2926, H.R. 5501) shows that Congress is more inclined to pay attention first to issues that are more spectacular and less arcane. Moreover, the arcaneness of digital asset regulatory issues is likely only to increase further, now that major industry players such as Coinbase and Andreessen Horowitz are starting to roll out their own regulatory proposals.
Digital Dollar vs. Digital Yuan
Impetus to pass legislation on another type of digital asset, a central bank digital currency (CBDC), may come from a different source: rivalry with China.
China established itself as a world leader in developing a CBDC with a pilot project launched in 2020, and in 2021, the People’s Bank of China announced that its CBDC will be used at the Beijing Winter Olympics in February 2022. Republican Senators responded by calling for the U.S. Olympic Committee to forbid use of China’s CBDC by U.S. athletes in Beijing and introducing a bill (S. 2543) to require a study of its national security implications.
The Beijing Olympics could motivate a legislative mandate to accelerate implementation of a U.S. digital dollar, which the Federal Reserve has been in the process of considering in 2021. Antecedents to such legislation already exist. A House bill sponsored by 46 Republicans (H.R. 4792) has a provision that would require the Treasury Department to assess China’s CBDC project and report on the status of Federal Reserve work on a CBDC, and the Beyer bill includes a provision amending the Federal Reserve Act to authorize issuing a digital dollar.
Both parties are likely to support creating a digital dollar. The Covid-19 pandemic made a digital dollar for delivery of relief payments a popular idea in 2020, and House Democrats introduced bills with provisions for creating one in 2020 and 2021. Bipartisan support for a bill on a digital dollar, based on concerns both foreign and domestic in nature, could result.
International rivalry and bipartisan support may make the digital dollar a gateway issue for digital asset legislation in 2022. Legislative work on a digital dollar may open the door for considering further digital asset issues—including the regulatory issues that have been emerging for years—in 2022 and beyond.

Rishi Dean
3 years ago
Coinbase's web3 app
Use popular Ethereum dapps with Coinbase’s new dapp wallet and browser
Tl;dr: This post highlights the ability to access web3 directly from your Coinbase app using our new dapp wallet and browser.
Decentralized autonomous organizations (DAOs) and decentralized finance (DeFi) have gained popularity in the last year (DAOs). The total value locked (TVL) of DeFi investments on the Ethereum blockchain has grown to over $110B USD, while NFTs sales have grown to over $30B USD in the last 12 months (LTM). New innovative real-world applications are emerging every day.
Today, a small group of Coinbase app users can access Ethereum-based dapps. Buying NFTs on Coinbase NFT and OpenSea, trading on Uniswap and Sushiswap, and borrowing and lending on Curve and Compound are examples.
Our new dapp wallet and dapp browser enable you to access and explore web3 directly from your Coinbase app.
Web3 in the Coinbase app
Users can now access dapps without a recovery phrase. This innovative dapp wallet experience uses Multi-Party Computation (MPC) technology to secure your on-chain wallet. This wallet's design allows you and Coinbase to share the 'key.' If you lose access to your device, the key to your dapp wallet is still safe and Coinbase can help recover it.
Set up your new dapp wallet by clicking the "Browser" tab in the Android app's navigation bar. Once set up, the Coinbase app's new dapp browser lets you search, discover, and use Ethereum-based dapps.
Looking forward
We want to enable everyone to seamlessly and safely participate in web3, and today’s launch is another step on that journey. We're rolling out the new dapp wallet and browser in the US on Android first to a small subset of users and plan to expand soon. Stay tuned!

The Verge
3 years ago
Bored Ape Yacht Club creator raises $450 million at a $4 billion valuation.
Yuga Labs, owner of three of the biggest NFT brands on the market, announced today a $450 million funding round. The money will be used to create a media empire based on NFTs, starting with games and a metaverse project.
The team's Otherside metaverse project is an MMORPG meant to connect the larger NFT universe. They want to create “an interoperable world” that is “gamified” and “completely decentralized,” says Wylie Aronow, aka Gordon Goner, co-founder of Bored Ape Yacht Club. “We think the real Ready Player One experience will be player run.”
Just a few weeks ago, Yuga Labs announced the acquisition of CryptoPunks and Meebits from Larva Labs. The deal brought together three of the most valuable NFT collections, giving Yuga Labs more IP to work with when developing games and metaverses. Last week, ApeCoin was launched as a cryptocurrency that will be governed independently and used in Yuga Labs properties.
Otherside will be developed by “a few different game studios,” says Yuga Labs CEO Nicole Muniz. The company plans to create development tools that allow NFTs from other projects to work inside their world. “We're welcoming everyone into a walled garden.”
However, Yuga Labs believes that other companies are approaching metaverse projects incorrectly, allowing the startup to stand out. People won't bond spending time in a virtual space with nothing going on, says Yuga Labs co-founder Greg Solano, aka Gargamel. Instead, he says, people bond when forced to work together.
In order to avoid getting smacked, Solano advises making friends. “We don't think a Zoom chat and walking around saying ‘hi' creates a deep social experience.” Yuga Labs refused to provide a release date for Otherside. Later this year, a play-to-win game is planned.
The funding round was led by Andreessen Horowitz, a major investor in the Web3 space. It previously backed OpenSea and Coinbase. Animoca Brands, Coinbase, and MoonPay are among those who have invested. Andreessen Horowitz general partner Chris Lyons will join Yuga Labs' board. The Financial Times broke the story last month.
"META IS A DOMINANT DIGITAL EXPERIENCE PROVIDER IN A DYSTOPIAN FUTURE."
This emerging [Web3] ecosystem is important to me, as it is to companies like Meta,” Chris Dixon, head of Andreessen Horowitz's crypto arm, tells The Verge. “In a dystopian future, Meta is the dominant digital experience provider, and it controls all the money and power.” (Andreessen Horowitz co-founder Marc Andreessen sits on Meta's board and invested early in Facebook.)
Yuga Labs has been profitable so far. According to a leaked pitch deck, the company made $137 million last year, primarily from its NFT brands, with a 95% profit margin. (Yuga Labs declined to comment on deck figures.)
But the company has built little so far. According to OpenSea data, it has only released one game for a limited time. That means Yuga Labs gets hundreds of millions of dollars to build a gaming company from scratch, based on a hugely lucrative art project.
Investors fund Yuga Labs based on its success. That's what they did, says Dixon, “they created a culture phenomenon”. But ultimately, the company is betting on the same thing that so many others are: that a metaverse project will be the next big thing. Now they must construct it.
You might also like

Steffan Morris Hernandez
3 years ago
10 types of cognitive bias to watch out for in UX research & design
10 biases in 10 visuals

Cognitive biases are crucial for UX research, design, and daily life. Our biases distort reality.
After learning about biases at my UX Research bootcamp, I studied Erika Hall's Just Enough Research and used the Nielsen Norman Group's wealth of information. 10 images show my findings.
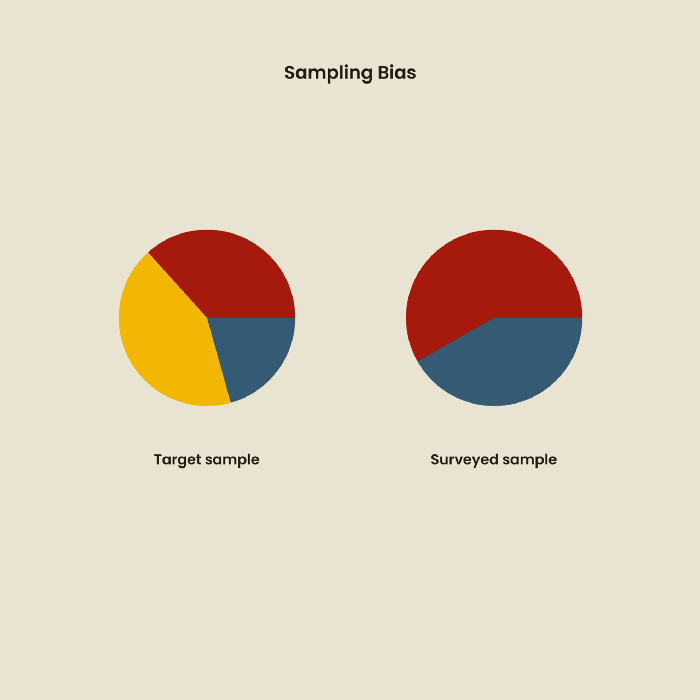
1. Bias in sampling
Misselection of target population members causes sampling bias. For example, you are building an app to help people with food intolerances log their meals and are targeting adult males (years 20-30), adult females (ages 20-30), and teenage males and females (ages 15-19) with food intolerances. However, a sample of only adult males and teenage females is biased and unrepresentative.
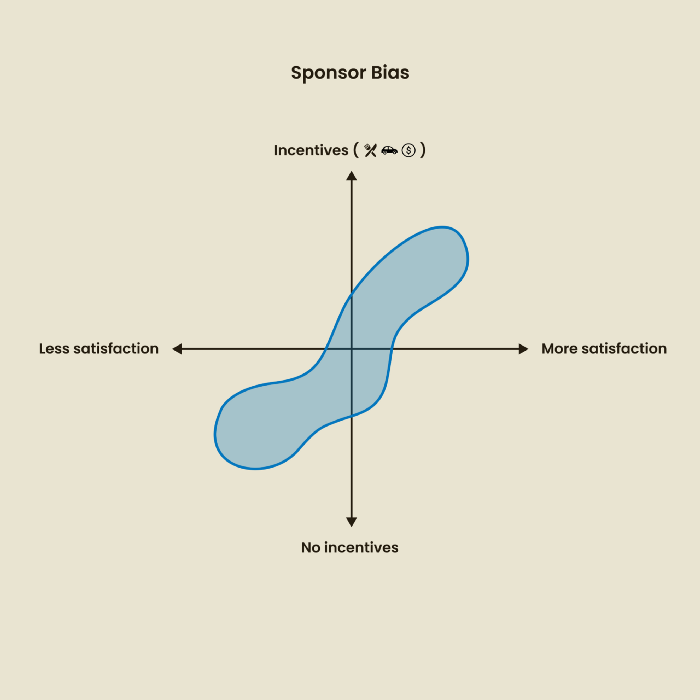
2. Sponsor Disparity
Sponsor bias occurs when a study's findings favor an organization's goals. Beware if X organization promises to drive you to their HQ, compensate you for your time, provide food, beverages, discounts, and warmth. Participants may endeavor to be neutral, but incentives and prizes may bias their evaluations and responses in favor of X organization.
In Just Enough Research, Erika Hall suggests describing the company's aims without naming it.
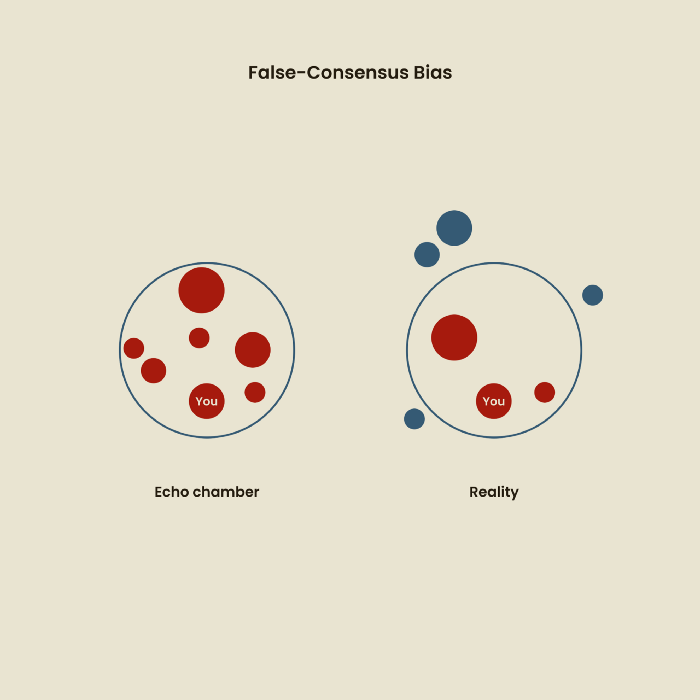
Third, False-Consensus Bias
False-consensus bias is when a person thinks others think and act the same way. For instance, if a start-up designs an app without researching end users' needs, it could fail since end users may have different wants. https://www.nngroup.com/videos/false-consensus-effect/
Working directly with the end user and employing many research methodologies to improve validity helps lessen this prejudice. When analyzing data, triangulation can boost believability.
Bias of the interviewer
I struggled with this bias during my UX research bootcamp interviews. Interviewing neutrally takes practice and patience. Avoid leading questions that structure the story since the interviewee must interpret them. Nodding or smiling throughout the interview may subconsciously influence the interviewee's responses.

The Curse of Knowledge
The curse of knowledge occurs when someone expects others understand a subject as well as they do. UX research interviews and surveys should reduce this bias because technical language might confuse participants and harm the research. Interviewing participants as though you are new to the topic may help them expand on their replies without being influenced by the researcher's knowledge.

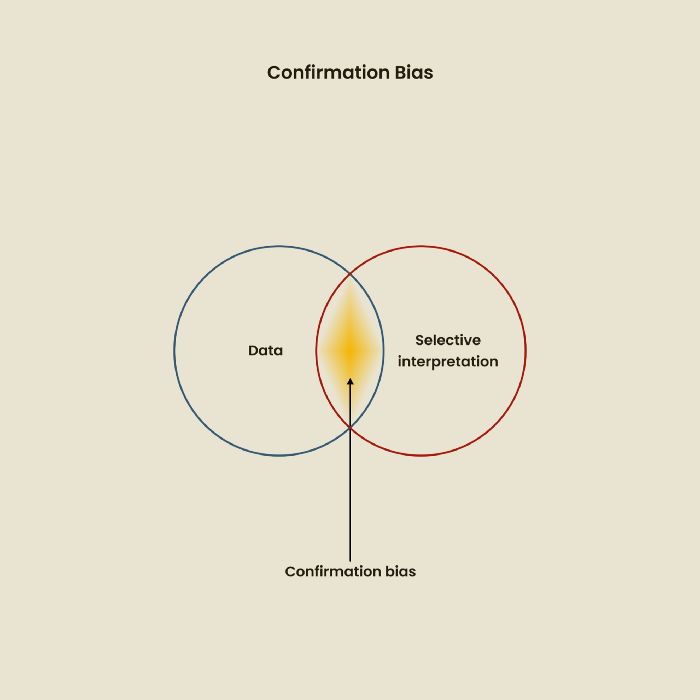
Confirmation Bias
Most prevalent bias. People highlight evidence that supports their ideas and ignore data that doesn't. The echo chamber of social media creates polarization by promoting similar perspectives.
A researcher with confirmation bias may dismiss data that contradicts their research goals. Thus, the research or product may not serve end users.
Design biases
UX Research design bias pertains to study construction and execution. Design bias occurs when data is excluded or magnified based on human aims, assumptions, and preferences.
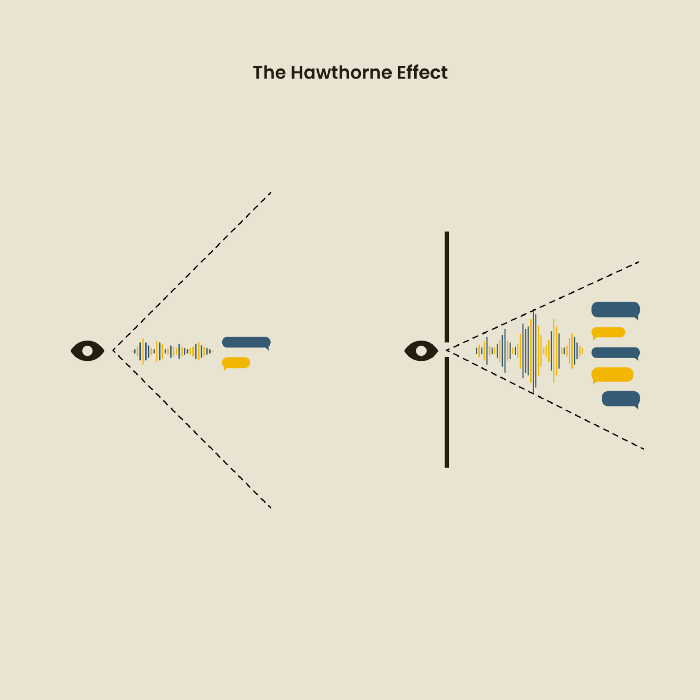
The Hawthorne Impact
Remember when you behaved differently while the teacher wasn't looking? When you behaved differently without your parents watching? A UX research study's Hawthorne Effect occurs when people modify their behavior because you're watching. To escape judgment, participants may act and speak differently.
To avoid this, researchers should blend into the background and urge subjects to act alone.
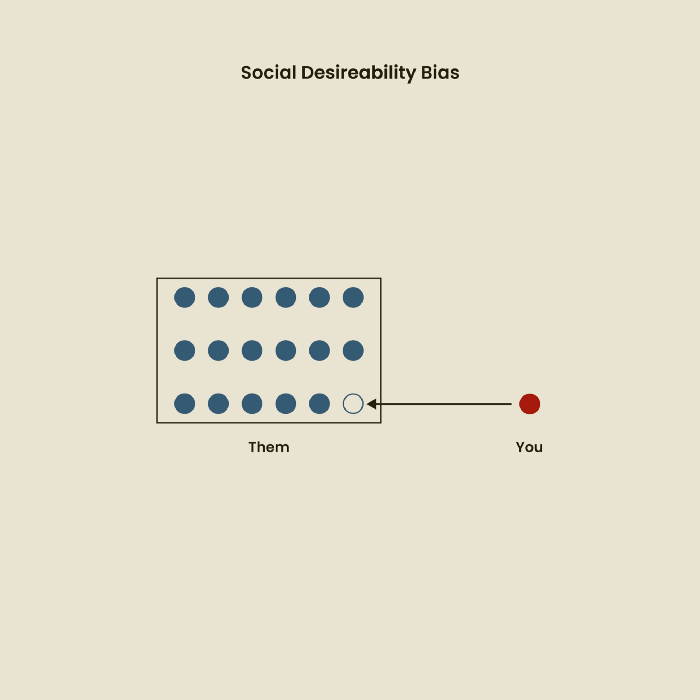
The bias against social desire
People want to belong to escape rejection and hatred. Research interviewees may mislead or slant their answers to avoid embarrassment. Researchers should encourage honesty and confidentiality in studies to address this. Observational research may reduce bias better than interviews because participants behave more organically.
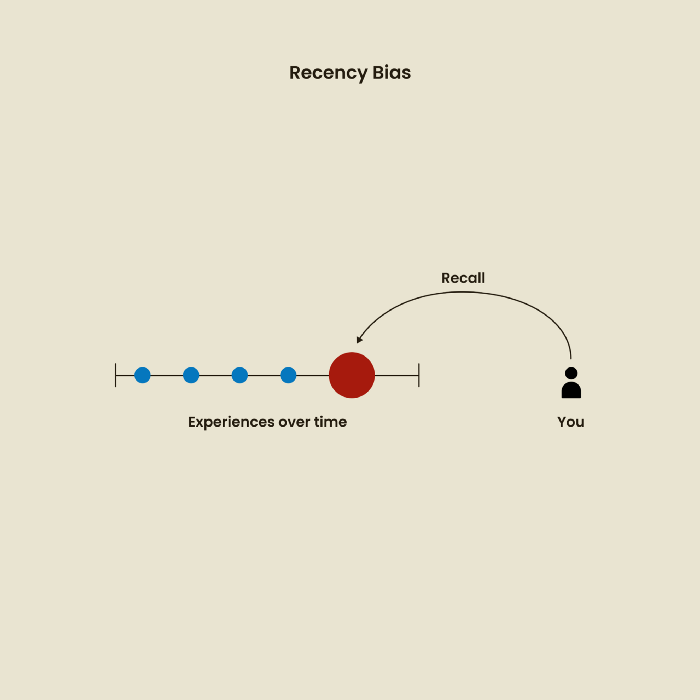
Relative Time Bias
Humans tend to appreciate recent experiences more. Consider school. Say you failed a recent exam but did well in the previous 7 exams. Instead, you may vividly recall the last terrible exam outcome.
If a UX researcher relies their conclusions on the most recent findings instead of all the data and results, recency bias might occur.
I hope you liked learning about UX design, research, and real-world biases.

Will Lockett
3 years ago
Russia's nukes may be useless

Russia's nuclear threat may be nullified by physics.
Putin seems nostalgic and wants to relive the Cold War. He's started a deadly war to reclaim the old Soviet state of Ukraine and is threatening the West with nuclear war. NATO can't risk starting a global nuclear war that could wipe out humanity to support Ukraine's independence as much as they want to. Fortunately, nuclear physics may have rendered Putin's nuclear weapons useless. However? How will Ukraine and NATO react?
To understand why Russia's nuclear weapons may be ineffective, we must first know what kind they are.
Russia has the world's largest nuclear arsenal, with 4,447 strategic and 1,912 tactical weapons (all of which are ready to be rolled out quickly). The difference between these two weapons is small, but it affects their use and logistics. Strategic nuclear weapons are ICBMs designed to destroy a city across the globe. Russia's ICBMs have many designs and a yield of 300–800 kilotonnes. 300 kilotonnes can destroy Washington. Tactical nuclear weapons are smaller and can be fired from artillery guns or small truck-mounted missile launchers, giving them a 1,500 km range. Instead of destroying a distant city, they are designed to eliminate specific positions, bases, or military infrastructure. They produce 1–50 kilotonnes.
These two nuclear weapons use different nuclear reactions. Pure fission bombs are compact enough to fit in a shell or small missile. All early nuclear weapons used this design for their fission bombs. This technology is inefficient for bombs over 50 kilotonnes. Larger bombs are thermonuclear. Thermonuclear weapons use a small fission bomb to compress and heat a hydrogen capsule, which undergoes fusion and releases far more energy than ignition fission reactions, allowing for effective giant bombs.
Here's Russia's issue.
A thermonuclear bomb needs deuterium (hydrogen with one neutron) and tritium (hydrogen with two neutrons). Because these two isotopes fuse at lower energies than others, the bomb works. One problem. Tritium is highly radioactive, with a half-life of only 12.5 years, and must be artificially made.
Tritium is made by irradiating lithium in nuclear reactors and extracting the gas. Tritium is one of the most expensive materials ever made, at $30,000 per gram.
Why does this affect Putin's nukes?
Thermonuclear weapons need tritium. Tritium decays quickly, so they must be regularly refilled at great cost, which Russia may struggle to do.
Russia has a smaller economy than New York, yet they are running an invasion, fending off international sanctions, and refining tritium for 4,447 thermonuclear weapons.
The Russian military is underfunded. Because the state can't afford it, Russian troops must buy their own body armor. Arguably, Putin cares more about the Ukraine conflict than maintaining his nuclear deterrent. Putin will likely lose power if he loses the Ukraine war.
It's possible that Putin halted tritium production and refueling to save money for Ukraine. His threats of nuclear attacks and escalating nuclear war may be a bluff.
This doesn't help Ukraine, sadly. Russia's tactical nuclear weapons don't need expensive refueling and will help with the invasion. So Ukraine still risks a nuclear attack. The bomb that destroyed Hiroshima was 15 kilotonnes, and Russia's tactical Iskander-K nuclear missile has a 50-kiloton yield. Even "little" bombs are deadly.
We can't guarantee it's happening in Russia. Putin may prioritize tritium. He knows the power of nuclear deterrence. Russia may have enough tritium for this conflict. Stockpiling a material with a short shelf life is unlikely, though.
This means that Russia's most powerful weapons may be nearly useless, but they may still be deadly. If true, this could allow NATO to offer full support to Ukraine and push the Russian tyrant back where he belongs. If Putin withholds funds from his crumbling military to maintain his nuclear deterrent, he may be willing to sink the ship with him. Let's hope the former.

Mircea Iosif
3 years ago
How To Start An Online Business That Will Be Profitable Without Investing A Lot Of Time

Don't know how to start an online business? Here's a guide. By following these recommendations, you can build a lucrative and profitable online business.
What Are Online Businesses Used For?
Most online businesses are websites. A self-created, self-managed website. You may sell things and services online.
To establish an internet business, you must locate a host and set up accounts with numerous companies. Once your accounts are set up, you may start publishing content and selling products or services.
How to Make Money from Your Online Business
Advertising and marketing are the best ways to make money online. You must develop strategies to contact new customers and generate leads. Make sure your website is search engine optimized so people can find you online.
Top 5 Online Business Tips for Startups:
1. Know your target audience's needs.
2. Make your website as appealing as possible.
3. Generate leads and sales with marketing.
4. Track your progress and learn from your mistakes to improve.
5. Be prepared to expand into new markets or regions.
How to Launch a Successful Online Business Without Putting in a Lot of Work
Build with a solid business model to start a profitable online business. By using these tips, you can start your online business without paying much.
First, develop a user-friendly website. You can use an internet marketing platform or create your own website. Once your website is live, optimize it for search engines and add relevant content.
Second, sell online. This can be done through ads or direct sales to website visitors. Finally, use social media to advertise your internet business. By accomplishing these things, you'll draw visitors to your website and make money.
When launching a business, invest long-term. This involves knowing your goals and how you'll pay for them. Volatility can have several effects on your business. If you offer things online, you may need to examine if the market is ready for them.
Invest wisely
Investing all your money in one endeavor can lead to too much risk and little ROI. Diversify your investments to take advantage of all available chances. So, your investments won't encounter unexpected price swings and you'll be immune to economic upheavals.
Financial news updates
When launching or running a thriving online business, financial news is crucial. By knowing current trends and upcoming developments, you can keep your business lucrative.
Keeping up with financial news can also help you avoid potential traps that could harm your bottom line. If you don't know about new legislation that could affect your industry, potential customers may choose another store when they learn about your business's problems.
Volatility ahead
You should expect volatility in the financial sector. Without a plan for coping with volatility, you could run into difficulty. If your organization relies on client input, you may not be able to exploit customer behavior shifts.
Your company could go bankrupt if you don't understand how fickle the stock market can be. By preparing for volatility, you can ensure your organization survives difficult times and market crashes.
Conclusion
Many internet businesses can be profitable. Start quickly with a few straightforward steps. Diversify your investments, follow financial news, and be prepared for volatility to develop a successful business.
Thanks for reading!
