Howey Test and Cryptocurrencies: 'Every ICO Is a Security'
What Is the Howey Test?
To determine whether a transaction qualifies as a "investment contract" and thus qualifies as a security, the Howey Test refers to the U.S. Supreme Court cass: the Securities Act of 1933 and the Securities Exchange Act of 1934. According to the Howey Test, an investment contract exists when "money is invested in a common enterprise with a reasonable expectation of profits from others' efforts."
The test applies to any contract, scheme, or transaction. The Howey Test helps investors and project backers understand blockchain and digital currency projects. ICOs and certain cryptocurrencies may be found to be "investment contracts" under the test.
Understanding the Howey Test
The Howey Test comes from the 1946 Supreme Court case SEC v. W.J. Howey Co. The Howey Company sold citrus groves to Florida buyers who leased them back to Howey. The company would maintain the groves and sell the fruit for the owners. Both parties benefited. Most buyers had no farming experience and were not required to farm the land.
The SEC intervened because Howey failed to register the transactions. The court ruled that the leaseback agreements were investment contracts.
This established four criteria for determining an investment contract. Investing contract:
- An investment of money
- n a common enterprise
- With the expectation of profit
- To be derived from the efforts of others
In the case of Howey, the buyers saw the transactions as valuable because others provided the labor and expertise. An income stream was obtained by only investing capital. As a result of the Howey Test, the transaction had to be registered with the SEC.
Howey Test and Cryptocurrencies
Bitcoin is notoriously difficult to categorize. Decentralized, they evade regulation in many ways. Regardless, the SEC is looking into digital assets and determining when their sale qualifies as an investment contract.
The SEC claims that selling digital assets meets the "investment of money" test because fiat money or other digital assets are being exchanged. Like the "common enterprise" test.
Whether a digital asset qualifies as an investment contract depends on whether there is a "expectation of profit from others' efforts."
For example, buyers of digital assets may be relying on others' efforts if they expect the project's backers to build and maintain the digital network, rather than a dispersed community of unaffiliated users. Also, if the project's backers create scarcity by burning tokens, the test is met. Another way the "efforts of others" test is met is if the project's backers continue to act in a managerial role.
These are just a few examples given by the SEC. If a project's success is dependent on ongoing support from backers, the buyer of the digital asset is likely relying on "others' efforts."
Special Considerations
If the SEC determines a cryptocurrency token is a security, many issues arise. It means the SEC can decide whether a token can be sold to US investors and forces the project to register.
In 2017, the SEC ruled that selling DAO tokens for Ether violated federal securities laws. Instead of enforcing securities laws, the SEC issued a warning to the cryptocurrency industry.
Due to the Howey Test, most ICOs today are likely inaccessible to US investors. After a year of ICOs, then-SEC Chair Jay Clayton declared them all securities.
SEC Chairman Gensler Agrees With Predecessor: 'Every ICO Is a Security'
Howey Test FAQs
How Do You Determine If Something Is a Security?
The Howey Test determines whether certain transactions are "investment contracts." Securities are transactions that qualify as "investment contracts" under the Securities Act of 1933 and the Securities Exchange Act of 1934.
The Howey Test looks for a "investment of money in a common enterprise with a reasonable expectation of profits from others' efforts." If so, the Securities Act of 1933 and the Securities Exchange Act of 1934 require disclosure and registration.
Why Is Bitcoin Not a Security?
Former SEC Chair Jay Clayton clarified in June 2018 that bitcoin is not a security: "Cryptocurrencies: Replace the dollar, euro, and yen with bitcoin. That type of currency is not a security," said Clayton.
Bitcoin, which has never sought public funding to develop its technology, fails the SEC's Howey Test. However, according to Clayton, ICO tokens are securities.
A Security Defined by the SEC
In the public and private markets, securities are fungible and tradeable financial instruments. The SEC regulates public securities sales.
The Supreme Court defined a security offering in SEC v. W.J. Howey Co. In its judgment, the court defines a security using four criteria:
- An investment contract's existence
- The formation of a common enterprise
- The issuer's profit promise
- Third-party promotion of the offering
Read original post.
More on Web3 & Crypto

Modern Eremite
3 years ago
The complete, easy-to-understand guide to bitcoin

Introduction
Markets rely on knowledge.
The internet provided practically endless knowledge and wisdom. Humanity has never seen such leverage. Technology's progress drives us to adapt to a changing world, changing our routines and behaviors.
In a digital age, people may struggle to live in the analogue world of their upbringing. Can those who can't adapt change their lives? I won't answer. We should teach those who are willing to learn, nevertheless. Unravel the modern world's riddles and give them wisdom.
Adapt or die . Accept the future or remain behind.
This essay will help you comprehend Bitcoin better than most market participants and the general public. Let's dig into Bitcoin.
Join me.

Ascension
Bitcoin.org was registered in August 2008. Bitcoin whitepaper was published on 31 October 2008. The document intrigued and motivated people around the world, including technical engineers and sovereignty seekers. Since then, Bitcoin's whitepaper has been read and researched to comprehend its essential concept.
I recommend reading the whitepaper yourself. You'll be able to say you read the Bitcoin whitepaper instead of simply Googling "what is Bitcoin" and reading the fundamental definition without knowing the revolution's scope. The article links to Bitcoin's whitepaper. To avoid being overwhelmed by the whitepaper, read the following article first.
Bitcoin isn't the first peer-to-peer digital currency. Hashcash or Bit Gold were once popular cryptocurrencies. These two Bitcoin precursors failed to gain traction and produce the network effect needed for general adoption. After many struggles, Bitcoin emerged as the most successful cryptocurrency, leading the way for others.
Satoshi Nakamoto, an active bitcointalk.org user, created Bitcoin. Satoshi's identity remains unknown. Satoshi's last bitcointalk.org login was 12 December 2010. Since then, he's officially disappeared. Thus, conspiracies and riddles surround Bitcoin's creators. I've heard many various theories, some insane and others well-thought-out.
It's not about who created it; it's about knowing its potential. Since its start, Satoshi's legacy has changed the world and will continue to.
Block-by-block blockchain
Bitcoin is a distributed ledger. What's the meaning?
Everyone can view all blockchain transactions, but no one can undo or delete them.
Imagine you and your friends routinely eat out, but only one pays. You're careful with money and what others owe you. How can everyone access the info without it being changed?

You'll keep a notebook of your evening's transactions. Everyone will take a page home. If one of you changed the page's data, the group would notice and reject it. The majority will establish consensus and offer official facts.
Miners add a new Bitcoin block to the main blockchain every 10 minutes. The appended block contains miner-verified transactions. Now that the next block has been added, the network will receive the next set of user transactions.
Bitcoin Proof of Work—prove you earned it
Any firm needs hardworking personnel to expand and serve clients. Bitcoin isn't that different.
Bitcoin's Proof of Work consensus system needs individuals to validate and create new blocks and check for malicious actors. I'll discuss Bitcoin's blockchain consensus method.
Proof of Work helps Bitcoin reach network consensus. The network is checked and safeguarded by CPU, GPU, or ASIC Bitcoin-mining machines (Application-Specific Integrated Circuit).
Every 10 minutes, miners are rewarded in Bitcoin for securing and verifying the network. It's unlikely you'll finish the block. Miners build pools to increase their chances of winning by combining their processing power.
In the early days of Bitcoin, individual mining systems were more popular due to high maintenance costs and larger earnings prospects. Over time, people created larger and larger Bitcoin mining facilities that required a lot of space and sophisticated cooling systems to keep machines from overheating.
Proof of Work is a vital part of the Bitcoin network, as network security requires the processing power of devices purchased with fiat currency. Miners must invest in mining facilities, which creates a new business branch, mining facilities ownership. Bitcoin mining is a topic for a future article.
More mining, less reward
Bitcoin is usually scarce.
Why is it rare? It all comes down to 21,000,000 Bitcoins.
Were all Bitcoins mined? Nope. Bitcoin's supply grows until it hits 21 million coins. Initially, 50BTC each block was mined, and each block took 10 minutes. Around 2140, the last Bitcoin will be mined.
But 50BTC every 10 minutes does not give me the year 2140. Indeed careful reader. So important is Bitcoin's halving process.
What is halving?
The block reward is halved every 210,000 blocks, which takes around 4 years. The initial payout was 50BTC per block and has been decreased to 25BTC after 210,000 blocks. First halving occurred on November 28, 2012, when 10,500,000 BTC (50%) had been mined. As of April 2022, the block reward is 6.25BTC and will be lowered to 3.125BTC by 19 March 2024.
The halving method is tied to Bitcoin's hashrate. Here's what "hashrate" means.
What if we increased the number of miners and hashrate they provide to produce a block every 10 minutes? Wouldn't we manufacture blocks faster?

Every 10 minutes, blocks are generated with little asymmetry. Due to the built-in adaptive difficulty algorithm, the overall hashrate does not affect block production time. With increased hashrate, it's harder to construct a block. We can estimate when the next halving will occur because 10 minutes per block is fixed.
Building with nodes and blocks
For someone new to crypto, the unusual terms and words may be overwhelming. You'll also find everyday words that are easy to guess or have a vague idea of what they mean, how they work, and what they do. Consider blockchain technology.
Nodes and blocks: Think about that for a moment. What is your first idea?
The blockchain is a chain of validated blocks added to the main chain. What's a "block"? What's inside?
The block is another page in the blockchain book that has been filled with transaction information and accepted by the majority.
We won't go into detail about what each block includes and how it's built, as long as you understand its purpose.
What about nodes?
Nodes, along with miners, verify the blockchain's state independently. But why?
To create a full blockchain node, you must download the whole Bitcoin blockchain and check every transaction against Bitcoin's consensus criteria.
What's Bitcoin's size?
In April 2022, the Bitcoin blockchain was 389.72GB.
Bitcoin's blockchain has miners and node runners.
Let's revisit the US gold rush. Miners mine gold with their own power (physical and monetary resources) and are rewarded with gold (Bitcoin). All become richer with more gold, and so does the country.
Nodes are like sheriffs, ensuring everything is done according to consensus rules and that there are no rogue miners or network users.
Lost and held bitcoin
Does the Bitcoin exchange price match each coin's price? How many coins remain after 21,000,000? 21 million or less?
Common reason suggests a 21 million-coin supply.
What if I lost 1BTC from a cold wallet?
What if I saved 1000BTC on paper in 2010 and it was damaged?
What if I mined Bitcoin in 2010 and lost the keys?
Satoshi Nakamoto's coins? Since then, those coins haven't moved.
How many BTC are truly in circulation?
Many people are trying to answer this question, and you may discover a variety of studies and individual research on the topic. Be cautious of the findings because they can't be evaluated and the statistics are hazy guesses.
On the other hand, we have long-term investors who won't sell their Bitcoin or will sell little amounts to cover mining or living needs.
The price of Bitcoin is determined by supply and demand on exchanges using liquid BTC. How many BTC are left after subtracting lost and non-custodial BTC?
We have significantly less Bitcoin in circulation than you think, thus the price may not reflect demand if we knew the exact quantity of coins available.
True HODLers and diamond-hand investors won't sell you their coins, no matter the market.
What's UTXO?
Unspent (U) Transaction (TX) Output (O)

Imagine taking a $100 bill to a store. After choosing a drink and munchies, you walk to the checkout to pay. The cashier takes your $100 bill and gives you $25.50 in change. It's in your wallet.
Is it simply 100$? No way.
The $25.50 in your wallet is unrelated to the $100 bill you used. Your wallet's $25.50 is just bills and coins. Your wallet may contain these coins and bills:
2x 10$ 1x 10$
1x 5$ or 3x 5$
1x 0.50$ 2x 0.25$
Any combination of coins and bills can equal $25.50. You don't care, and I'd wager you've never ever considered it.
That is UTXO. Now, I'll detail the Bitcoin blockchain and how UTXO works, as it's crucial to know what coins you have in your (hopefully) cold wallet.
You purchased 1BTC. Is it all? No. UTXOs equal 1BTC. Then send BTC to a cold wallet. Say you pay 0.001BTC and send 0.999BTC to your cold wallet. Is it the 1BTC you got before? Well, yes and no. The UTXOs are the same or comparable as before, but the blockchain address has changed. It's like if you handed someone a wallet, they removed the coins needed for a network charge, then returned the rest of the coins and notes.
UTXO is a simple concept, but it's crucial to grasp how it works to comprehend dangers like dust attacks and how coins may be tracked.
Lightning Network: fast cash
You've probably heard of "Layer 2 blockchain" projects.
What does it mean?
Layer 2 on a blockchain is an additional layer that increases the speed and quantity of transactions per minute and reduces transaction fees.
Imagine going to an obsolete bank to transfer money to another account and having to pay a charge and wait. You can transfer funds via your bank account or a mobile app without paying a fee, or the fee is low, and the cash appear nearly quickly. Layer 1 and 2 payment systems are different.
Layer 1 is not obsolete; it merely has more essential things to focus on, including providing the blockchain with new, validated blocks, whereas Layer 2 solutions strive to offer Layer 1 with previously processed and verified transactions. The primary blockchain, Bitcoin, will only receive the wallets' final state. All channel transactions until shutting and balancing are irrelevant to the main chain.
Layer 2 and the Lightning Network's goal are now clear. Most Layer 2 solutions on multiple blockchains are created as blockchains, however Lightning Network is not. Remember the following remark, as it best describes Lightning.

Lightning Network connects public and private Bitcoin wallets.
Opening a private channel with another wallet notifies just two parties. The creation and opening of a public channel tells the network that anyone can use it.
Why create a public Lightning Network channel?
Every transaction through your channel generates fees.
Money, if you don't know.
See who benefits when in doubt.
Anonymity, huh?
Bitcoin anonymity? Bitcoin's anonymity was utilized to launder money.
Well… You've heard similar stories. When you ask why or how it permits people to remain anonymous, the conversation ends as if it were just a story someone heard.
Bitcoin isn't private. Pseudonymous.
What if someone tracks your transactions and discovers your wallet address? Where is your anonymity then?

Bitcoin is like bulletproof glass storage; you can't take or change the money. If you dig and analyze the data, you can see what's inside.
Every online action leaves a trace, and traces may be tracked. People often forget this guideline.
A tool like that can help you observe what the major players, or whales, are doing with their coins when the market is uncertain. Many people spend time analyzing on-chain data. Worth it?
Ask yourself a question. What are the big players' options? Do you think they're letting you see their wallets for a small on-chain data fee?
Instead of short-term behaviors, focus on long-term trends.
More wallet transactions leave traces. Having nothing to conceal isn't a defect. Can it lead to regulating Bitcoin so every transaction is tracked like in banks today?
But wait. How can criminals pay out Bitcoin? They're doing it, aren't they?
Mixers can anonymize your coins, letting you to utilize them freely. This is not a guide on how to make your coins anonymous; it could do more harm than good if you don't know what you're doing.
Remember, being anonymous attracts greater attention.
Bitcoin isn't the only cryptocurrency we can use to buy things. Using cryptocurrency appropriately can provide usability and anonymity. Monero (XMR), Zcash (ZEC), and Litecoin (LTC) following the Mimblewimble upgrade are examples.
Summary
Congratulations! You've reached the conclusion of the article and learned about Bitcoin and cryptocurrency. You've entered the future.
You know what Bitcoin is, how its blockchain works, and why it's not anonymous. I bet you can explain Lightning Network and UTXO to your buddies.
Markets rely on knowledge. Prepare yourself for success before taking the first step. Let your expertise be your edge.
This article is a summary of this one.

Tim Denning
3 years ago
The Dogecoin millionaire mysteriously disappeared.
The American who bought a meme cryptocurrency.

Cryptocurrency is the financial underground.
I love it. But there’s one thing I hate: scams. Over the last few years the Dogecoin cryptocurrency saw massive gains.
Glauber Contessoto overreacted. He shared his rags-to-riches cryptocurrency with the media.
He's only wealthy on paper. No longer Dogecoin millionaire.
Here's what he's doing now. It'll make you rethink cryptocurrency investing.
Strange beginnings
Glauber once had a $36,000-a-year job.
He grew up poor and wanted to make his mother proud. Tesla was his first investment. He bought GameStop stock after Reddit boosted it.
He bought whatever was hot.
He was a young investor. Memes, not research, influenced his decisions.
Elon Musk (aka Papa Elon) began tweeting about Dogecoin.
Doge is a 2013 cryptocurrency. One founder is Australian. He insists it's funny.
He was shocked anyone bought it LOL.
Doge is a Shiba Inu-themed meme. Now whenever I see a Shiba Inu, I think of Doge.
Elon helped drive up the price of Doge by talking about it in 2020 and 2021 (don't take investment advice from Elon; he's joking and gaslighting you).
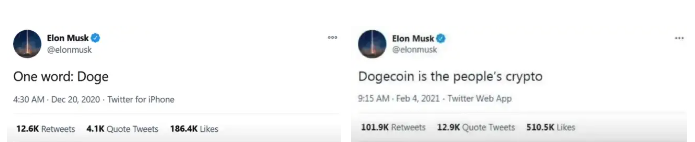
Glauber caved. He invested everything in Doge. He borrowed from family and friends. He maxed out his credit card to buy more Doge. Yuck.
Internet dubbed him a genius. Slumdog millionaire and The Dogefather were nicknames. Elon pumped Doge on social media.
Good times.
From $180,000 to $1,000,000+
TikTok skyrocketed Doge's price.
Reddit fueled up. Influencers recommended buying Doge because of its popularity. Glauber's motto:
Scared money doesn't earn.
Glauber was no broke ass anymore.
His $180,000 Dogecoin investment became $1M. He championed investing. He quit his dumb job like a rebellious millennial.
A puppy dog meme captivated the internet.
Rise and fall
Whenever I invest in anything I ask myself “what utility does this have?”
Dogecoin is useless.
You buy it for the cute puppy face and hope others will too, driving up the price. All cryptocurrencies fell in 2021's second half.
Central banks raised interest rates, and inflation became a pain.
Dogecoin fell more than others. 90% decline.
Glauber’s Dogecoin is now worth $323K. Still no sales. His dog god is unshakeable. Confidence rocks. Dogecoin millionaire recently said...
“I should have sold some.”
Yes, sir.
He now avoids speculative cryptocurrencies like Dogecoin and focuses on Bitcoin and Ethereum.
I've long said this. Starbucks is building on Ethereum.
It's useful. Useful. Developers use Ethereum daily. Investing makes you wiser over time, like the Dogecoin millionaire.
When risk b*tch slaps you, humility follows, as it did for me when I lost money.
You have to lose money to make money. Few understand.
Dogecoin's omissions
You might be thinking Dogecoin is crap.
I'll take a contrarian stance. Dogecoin does nothing, but it has a strong community. Dogecoin dominates internet memes.
It's silly.
Not quite. The message of crypto that many people forget is that it’s a change in business model.
Businesses create products and services, then advertise to find customers. Crypto Web3 works backwards. A company builds a fanbase but sells them nothing.
Once the community reaches MVC (minimum viable community), a business can be formed.
Community members are relational versus transactional. They're invested in a cause and care about it (typically ownership in the business via crypto).
In this new world, Dogecoin has the most important feature.
Summary
While Dogecoin does have a community I still dislike it.
It's all shady. Anything Elon Musk recommends is a bad investment (except SpaceX & Tesla are great companies).
Dogecoin Millionaire has wised up and isn't YOLOing into more dog memes.
Don't follow the crowd or the hype. Investing is a long-term sport based on fundamentals and research.
Since Ethereum's inception, I've spent 10,000 hours researching.
Dogecoin will be the foundation of something new, like Pets.com at the start of the dot-com revolution. But I doubt Doge will boom.
Be safe!
David Z. Morris
3 years ago
FTX's crash was no accident, it was a crime

Sam Bankman Fried (SDBF) is a legendary con man. But the NYT might not tell you that...
Since SBF's empire was revealed to be a lie, mainstream news organizations and commentators have failed to give readers a straightforward assessment. The New York Times and Wall Street Journal have uncovered many key facts about the scandal, but they have also soft-peddled Bankman-Fried's intent and culpability.
It's clear that the FTX crypto exchange and Alameda Research committed fraud to steal money from users and investors. That’s why a recent New York Times interview was widely derided for seeming to frame FTX’s collapse as the result of mismanagement rather than malfeasance. A Wall Street Journal article lamented FTX's loss of charitable donations, bolstering Bankman's philanthropic pose. Matthew Yglesias, court chronicler of the neoliberal status quo, seemed to whitewash his own entanglements by crediting SBF's money with helping Democrats in 2020 – sidestepping the likelihood that the money was embezzled.
Many outlets have called what happened to FTX a "bank run" or a "run on deposits," but Bankman-Fried insists the company was overleveraged and disorganized. Both attempts to frame the fallout obscure the core issue: customer funds misused.
Because banks lend customer funds to generate returns, they can experience "bank runs." If everyone withdraws at once, they can experience a short-term cash crunch but there won't be a long-term problem.
Crypto exchanges like FTX aren't banks. They don't do bank-style lending, so a withdrawal surge shouldn't strain liquidity. FTX promised customers it wouldn't lend or use their crypto.
Alameda's balance sheet blurs SBF's crypto empire.
The funds were sent to Alameda Research, where they were apparently gambled away. This is massive theft. According to a bankruptcy document, up to 1 million customers could be affected.
In less than a month, reporting and the bankruptcy process have uncovered a laundry list of decisions and practices that would constitute financial fraud if FTX had been a U.S.-regulated entity, even without crypto-specific rules. These ploys may be litigated in U.S. courts if they enabled the theft of American property.
The list is very, very long.
The many crimes of Sam Bankman-Fried and FTX
At the heart of SBF's fraud are the deep and (literally) intimate ties between FTX and Alameda Research, a hedge fund he co-founded. An exchange makes money from transaction fees on user assets, but Alameda trades and invests its own funds.
Bankman-Fried called FTX and Alameda "wholly separate" and resigned as Alameda's CEO in 2019. The two operations were closely linked. Bankman-Fried and Alameda CEO Caroline Ellison were romantically linked.
These circumstances enabled SBF's sin. Within days of FTX's first signs of weakness, it was clear the exchange was funneling customer assets to Alameda for trading, lending, and investing. Reuters reported on Nov. 12 that FTX sent $10 billion to Alameda. As much as $2 billion was believed to have disappeared after being sent to Alameda. Now the losses look worse.
It's unclear why those funds were sent to Alameda or when Bankman-Fried betrayed his depositors. On-chain analysis shows most FTX to Alameda transfers occurred in late 2021, and bankruptcy filings show both lost $3.7 billion in 2021.
SBF's companies lost millions before the 2022 crypto bear market. They may have stolen funds before Terra and Three Arrows Capital, which killed many leveraged crypto players.
FTT loans and prints
CoinDesk's report on Alameda's FTT holdings ignited FTX and Alameda Research. FTX created this instrument, but only a small portion was traded publicly; FTX and Alameda held the rest. These holdings were illiquid, meaning they couldn't be sold at market price. Bankman-Fried valued its stock at the fictitious price.
FTT tokens were reportedly used as collateral for loans, including FTX loans to Alameda. Close ties between FTX and Alameda made the FTT token harder or more expensive to use as collateral, reducing the risk to customer funds.
This use of an internal asset as collateral for loans between clandestinely related entities is similar to Enron's 1990s accounting fraud. These executives served 12 years in prison.
Alameda's margin liquidation exemption
Alameda Research had a "secret exemption" from FTX's liquidation and margin trading rules, according to legal filings by FTX's new CEO.
FTX, like other crypto platforms and some equity or commodity services, offered "margin" or loans for trades. These loans are usually collateralized, meaning borrowers put up other funds or assets. If a margin trade loses enough money, the exchange will sell the user's collateral to pay off the initial loan.
Keeping asset markets solvent requires liquidating bad margin positions. Exempting Alameda would give it huge advantages while exposing other FTX users to hidden risks. Alameda could have kept losing positions open while closing out competitors. Alameda could lose more on FTX than it could pay back, leaving a hole in customer funds.
The exemption is criminal in multiple ways. FTX was fraudulently marketed overall. Instead of a level playing field, there were many customers.
Above them all, with shotgun poised, was Alameda Research.
Alameda front-running FTX listings
Argus says there's circumstantial evidence that Alameda Research had insider knowledge of FTX's token listing plans. Alameda was able to buy large amounts of tokens before the listing and sell them after the price bump.
If true, these claims would be the most brazenly illegal of Alameda and FTX's alleged shenanigans. Even if the tokens aren't formally classified as securities, insider trading laws may apply.
In a similar case this year, an OpenSea employee was charged with wire fraud for allegedly insider trading. This employee faces 20 years in prison for front-running monkey JPEGs.
Huge loans to executives
Alameda Research reportedly lent FTX executives $4.1 billion, including massive personal loans. Bankman-Fried received $1 billion in personal loans and $2.3 billion for an entity he controlled, Paper Bird. Nishad Singh, director of engineering, was given $543 million, and FTX Digital Markets co-CEO Ryan Salame received $55 million.
FTX has more smoking guns than a Texas shooting range, but this one is the smoking bazooka – a sign of criminal intent. It's unclear how most of the personal loans were used, but liquidators will have to recoup the money.
The loans to Paper Bird were even more worrisome because they created another related third party to shuffle assets. Forbes speculates that some Paper Bird funds went to buy Binance's FTX stake, and Paper Bird committed hundreds of millions to outside investments.
FTX Inner Circle: Who's Who
That included many FTX-backed VC funds. Time will tell if this financial incest was criminal fraud. It fits Bankman-pattern Fried's of using secret flows, leverage, and funny money to inflate asset prices.
FTT or loan 'bailouts'
Also. As the crypto bear market continued in 2022, Bankman-Fried proposed bailouts for bankrupt crypto lenders BlockFi and Voyager Digital. CoinDesk was among those deceived, welcoming SBF as a J.P. Morgan-style sector backstop.
In a now-infamous interview with CNBC's "Squawk Box," Bankman-Fried referred to these decisions as bets that may or may not pay off.
But maybe not. Bloomberg's Matt Levine speculated that FTX backed BlockFi with FTT money. This Monopoly bailout may have been intended to hide FTX and Alameda liabilities that would have been exposed if BlockFi went bankrupt sooner. This ploy has no name, but it echoes other corporate frauds.
Secret bank purchase
Alameda Research invested $11.5 million in the tiny Farmington State Bank, doubling its net worth. As a non-U.S. entity and an investment firm, Alameda should have cleared regulatory hurdles before acquiring a U.S. bank.
In the context of FTX, the bank's stake becomes "ominous." Alameda and FTX could have done more shenanigans with bank control. Compare this to the Bank for Credit and Commerce International's failed attempts to buy U.S. banks. BCCI was even nefarious than FTX and wanted to buy U.S. banks to expand its money-laundering empire.
The mainstream's mistakes
These are complex and nuanced forms of fraud that echo traditional finance models. This obscurity helped Bankman-Fried masquerade as an honest player and likely kept coverage soft after the collapse.
Bankman-Fried had a scruffy, nerdy image, like Mark Zuckerberg and Adam Neumann. In interviews, he spoke nonsense about an industry full of jargon and complicated tech. Strategic donations and insincere ideological statements helped him gain political and social influence.
SBF' s'Effective' Altruism Blew Up FTX
Bankman-Fried has continued to muddy the waters with disingenuous letters, statements, interviews, and tweets since his con collapsed. He's tried to portray himself as a well-intentioned but naive kid who made some mistakes. This is a softer, more pernicious version of what Trump learned from mob lawyer Roy Cohn. Bankman-Fried doesn't "deny, deny, deny" but "confuse, evade, distort."
It's mostly worked. Kevin O'Leary, who plays an investor on "Shark Tank," repeats Bankman-SBF's counterfactuals. O'Leary called Bankman-Fried a "savant" and "probably one of the most accomplished crypto traders in the world" in a Nov. 27 interview with Business Insider, despite recent data indicating immense trading losses even when times were good.
O'Leary's status as an FTX investor and former paid spokesperson explains his continued affection for Bankman-Fried despite contradictory evidence. He's not the only one promoting Bankman-Fried. The disgraced son of two Stanford law professors will defend himself at Wednesday's DealBook Summit.
SBF's fraud and theft rival those of Bernie Madoff and Jho Low. Whether intentionally or through malign ineptitude, the fraud echoes Worldcom and Enron.
The Perverse Impacts of Anti-Money-Laundering
The principals in all of those scandals wound up either sentenced to prison or on the run from the law. Sam Bankman-Fried clearly deserves to share their fate.
Read the full article here.
You might also like

obimy.app
3 years ago
How TikTok helped us grow to 6 million users
This resulted to obimy's new audience.

Hi! obimy's official account. Here, we'll teach app developers and marketers. In 2022, our downloads increased dramatically, so we'll share what we learned.
obimy is what we call a ‘senseger’. It's a new method to communicate digitally. Instead of text, obimy users connect through senses and moods. Feeling playful? Flirt with your partner, pat a pal, or dump water on a classmate. Each feeling is an interactive animation with vibration. It's a wordless app. App Store and Google Play have obimy.
We had 20,000 users in 2022. Two to five thousand of them opened the app monthly. Our DAU metric was 500.
We have 6 million users after 6 months. 500,000 individuals use obimy daily. obimy was the top lifestyle app this week in the U.S.
And TikTok helped.
TikTok fuels obimys' growth. It's why our app exploded. How and what did we learn? Our Head of Marketing, Anastasia Avramenko, knows.
our actions prior to TikTok
We wanted to achieve product-market fit through organic expansion. Quora, Reddit, Facebook Groups, Facebook Ads, Google Ads, Apple Search Ads, and social media activity were tested. Nothing worked. Our CPI was sometimes $4, so unit economics didn't work.
We studied our markets and made audience hypotheses. We promoted our goods and studied our audience through social media quizzes. Our target demographic was Americans in long-distance relationships. I designed quizzes like Test the Strength of Your Relationship to better understand the user base. After each quiz, we encouraged users to download the app to enhance their connection and bridge the distance.
We got 1,000 responses for $50. This helped us comprehend the audience's grief and coping strategies (aka our rivals). I based action items on answers given. If you can't embrace a loved one, use obimy.
We also tried Facebook and Google ads. From the start, we knew it wouldn't work.
We were desperate to discover a free way to get more users.
Our journey to TikTok
TikTok is a great venue for emerging creators. It also helped reach people. Before obimy, my TikTok videos garnered 12 million views without sponsored promotion.
We had to act. TikTok was required.

I wasn't a TikTok user before obimy. Initially, I uploaded promotional content. Call-to-actions appear strange next to dancing challenges and my money don't jiggle jiggle. I learned TikTok. Watch TikTok for an hour was on my to-do list. What a dream job!
Our most popular movies presented the app alongside text outlining what it does. We started promoting them in Europe and the U.S. and got a 16% CTR and $1 CPI, an improvement over our previous efforts.
Somehow, we were expanding. So we came up with new hypotheses, calls to action, and content.
Four months passed, yet we saw no organic growth.
Russia attacked Ukraine.
Our app aimed to be helpful. For now, we're focusing on our Ukrainian audience. I posted sloppy TikToks illustrating how obimy can help during shelling or air raids.
In two hours, Kostia sent me our visitor count. Our servers crashed.
Initially, we had several thousand daily users. Over 200,000 users joined obimy in a week. They posted obimy videos on TikTok, drawing additional users. We've also resumed U.S. video promotion.
We gained 2,000,000 new members with less than $100 in ads, primarily in the U.S. and U.K.
TikTok helped.
The figures
We were confident we'd chosen the ideal tool for organic growth.
Over 45 million people have viewed our own videos plus a ton of user-generated content with the hashtag #obimy.
About 375 thousand people have liked all of our individual videos.
The number of downloads and the virality of videos are directly correlated.
Where are we now?
TikTok fuels our organic growth. We post 56 videos every week and pay to promote viral content.
We use UGC and influencers. We worked with Universal Music Italy on Eurovision. They offered to promote us through their million-follower TikTok influencers. We thought their followers would improve our audience, but it didn't matter. Integration didn't help us. Users that share obimy videos with their followers can reach several million views, which affects our download rate.
After the dust settled, we determined our key audience was 13-18-year-olds. They want to express themselves, but it's sometimes difficult. We're searching for methods to better engage with our users. We opened a Discord server to discuss anime and video games and gather app and content feedback.
TikTok helps us test product updates and hypotheses. Example: I once thought we might raise MAU by prompting users to add strangers as friends. Instead of asking our team to construct it, I made a TikTok urging users to share invite URLs. Users share links under every video we upload, embracing people worldwide.
Key lessons
Don't direct-sell. TikTok isn't for Instagram, Facebook, or YouTube promo videos. Conventional advertisements don't fit. Most users will swipe up and watch humorous doggos.
More product videos are better. Finally. So what?
Encourage interaction. Tagging friends in comments or making videos with the app promotes it more than any marketing spend.
Be odd and risqué. A user mistakenly sent a French kiss to their mom in one of our most popular videos.
TikTok helps test hypotheses and build your user base. It also helps develop apps. In our upcoming blog, we'll guide you through obimy's design revisions based on TikTok. Follow us on Twitter, Instagram, and TikTok.

Andy Walker
3 years ago
Why personal ambition and poor leadership caused Google layoffs

Google announced 6% layoffs recently (or 12,000 people). This aligns it with most tech companies. A publicly contrite CEO explained that they had overhired during the COVID-19 pandemic boom and had to address it, but they were sorry and took full responsibility. I thought this was "bullshit" too. Meta, Amazon, Microsoft, and others must feel similarly. I spent 10 years at Google, and these things don't reflect well on the company's leaders.
All publicly listed companies have a fiduciary duty to act in the best interests of their shareholders. Dodge vs. Ford Motor Company established this (1919). Henry Ford wanted to reduce shareholder payments to offer cheaper cars and better wages. Ford stated.
My ambition is to employ still more men, to spread the benefits of this industrial system to the greatest possible number, to help them build up their lives and their homes. To do this we are putting the greatest share of our profits back in the business.
The Dodge brothers, who owned 10% of Ford, opposed this and sued Ford for the payments to start their own company. They won, preventing Ford from raising prices or salaries. If you have a vocal group of shareholders with the resources to sue you, you must prove you are acting in their best interests. Companies prioritize shareholders. Giving activist investors a stick to threaten you almost enshrines short-term profit over long-term thinking.
This underpins Google's current issues. Institutional investors who can sue Google see it as a wasteful company they can exploit. That doesn't mean you have to maximize profits (thanks to those who pointed out my ignorance of US corporate law in the comments and on HN), but it allows pressure. I feel for those navigating this. This is about unrestrained capitalism.
When Google went public, Larry Page and Sergey Brin knew the risks and worked hard to keep control. In their Founders' Letter to investors, they tried to set expectations for the company's operations.
Our long-term focus as a private company has paid off. Public companies do the same. We believe outside pressures lead companies to sacrifice long-term opportunities to meet quarterly market expectations.
The company has transformed since that letter. The company has nearly 200,000 full-time employees and a trillion-dollar market cap. Large investors have bought company stock because it has been a good long-term bet. Why are they restless now?
Other big tech companies emerged and fought for top talent. This has caused rising compensation packages. Google has also grown rapidly (roughly 22,000 people hired to the end of 2022). At $300,000 median compensation, those 22,000 people added $6.6 billion in salary overheads in 2022. Exorbitant. If the company still makes $16 billion every quarter, maybe not. Investors wonder if this value has returned.
Investors are right. Google uses people wastefully. However, by bluntly reducing headcount, they're not addressing the root causes and hurting themselves. No studies show that downsizing this way boosts productivity. There is plenty of evidence that they'll lose out because people will be risk-averse and distrust their leadership.
The company's approach also stinks. Finding out that you no longer have a job because you can’t log in anymore (sometimes in cases where someone is on call for protecting your production systems) is no way to fire anyone. Being with a narcissistic sociopath is like being abused. First, you receive praise and fancy perks for making the cut. You're fired by text and ghosted. You're told to appreciate the generous severance package. This firing will devastate managers and teams. This type of firing will take years to recover self-esteem. Senior management contributed to this. They chose the expedient answer, possibly by convincing themselves they were managing risk and taking the Macbeth approach of “If it were done when ’tis done, then ’twere well It were done quickly”.
Recap. Google's leadership did a stupid thing—mass firing—in a stupid way. How do we get rid of enough people to make investors happier? and "have 6% less people." Empathetic leaders should not emulate Elon Musk. There is no humane way to fire 12,000 people, but there are better ways. Why is Google so wasteful?
Ambition answers this. There aren't enough VP positions for a group of highly motivated, ambitious, and (increasingly) ruthless people. I’ve loitered around the edges of this world and a large part of my value was to insulate my teams from ever having to experience it. It’s like Game of Thrones played out through email and calendar and over video call.
Your company must look a certain way to be promoted to director or higher. You need the right people at the right levels under you. Long-term, growing your people will naturally happen if you're working on important things. This takes time, and you're never more than 6–18 months from a reorg that could start you over. Ambitious people also tend to be impatient. So, what do you do?
Hiring and vanity projects. To shape your company, you hire at the right levels. You value vanity metrics like active users over product utility. Your promo candidates get through by subverting the promotion process. In your quest for growth, you avoid performance managing people out. You avoid confronting toxic peers because you need their support for promotion. Your cargo cult gets you there.
Its ease makes Google wasteful. Since they don't face market forces, the employees don't see it as a business. Why would you do when the ads business is so profitable? Complacency causes senior leaders to prioritize their own interests. Empires collapse. Personal ambition often trumped doing the right thing for users, the business, or employees. Leadership's ambition over business is the root cause. Vanity metrics, mass hiring, and vague promises have promoted people to VP. Google goes above and beyond to protect senior leaders.
The decision-makers and beneficiaries are not the layoffees. Stock price increase beneficiaries. The people who will post on LinkedIn how it is about misjudging the market and how they’re so sorry and take full responsibility. While accumulating wealth, the dark room dwellers decide who stays and who goes. The billionaire investors. Google should start by addressing its bloated senior management, but — as they say — turkeys don't vote for Christmas. It should examine its wastefulness and make tough choices to fix it. A 6% cut is a blunt tool that admits you're not running your business properly. why aren’t the people running the business the ones shortly to be entering the job market?
This won't fix Google's wastefulness. The executives may never regain trust after their approach. Suppressed creativity. Business won't improve. Google will have lost its founding vision and us all. Large investors know they can force Google's CEO to yield. The rich will get richer and rationalize leaving 12,000 people behind. Cycles repeat.
It doesn’t have to be this way. In 2013, Nintendo's CEO said he wouldn't fire anyone for shareholders. Switch debuted in 2017. Nintendo's stock has increased by nearly five times, or 19% a year (including the drop most of the stock market experienced last year). Google wasted 12,000 talented people. To please rich people.

Sanjay Priyadarshi
3 years ago
Meet a Programmer Who Turned Down Microsoft's $10,000,000,000 Acquisition Offer
Failures inspire young developers

Jason citron created many products.
These products flopped.
Microsoft offered $10 billion for one of these products.
He rejected the offer since he was so confident in his success.
Let’s find out how he built a product that is currently valued at $15 billion.
Early in his youth, Jason began learning to code.
Jason's father taught him programming and IT.
His father wanted to help him earn money when he needed it.
Jason created video games and websites in high school.
Jason realized early on that his IT and programming skills could make him money.
Jason's parents misjudged his aptitude for programming.
Jason frequented online programming communities.
He looked for web developers. He created websites for those people.
His parents suspected Jason sold drugs online. When he said he used programming to make money, they were shocked.
They helped him set up a PayPal account.
Florida higher education to study video game creation
Jason never attended an expensive university.
He studied game design in Florida.
“Higher Education is an interesting part of society… When I work with people, the school they went to never comes up… only thing that matters is what can you do…At the end of the day, the beauty of silicon valley is that if you have a great idea and you can bring it to the life, you can convince a total stranger to give you money and join your project… This notion that you have to go to a great school didn’t end up being a thing for me.”
Jason's life was altered by Steve Jobs' keynote address.
After graduating, Jason joined an incubator.
Jason created a video-dating site first.
Bad idea.
Nobody wanted to use it when it was released, so they shut it down.
He made a multiplayer game.
It was released on Bebo. 10,000 people played it.
When Steve Jobs unveiled the Apple app store, he stopped playing.
The introduction of the app store resembled that of a new gaming console.
Jason's life altered after Steve Jobs' 2008 address.
“Whenever a new video game console is launched, that’s the opportunity for a new video game studio to get started, it’s because there aren’t too many games available…When a new PlayStation comes out, since it’s a new system, there’s only a handful of titles available… If you can be a launch title you can get a lot of distribution.”
Apple's app store provided a chance to start a video game company.
They released an app after 5 months of work.
Aurora Feint is the game.
Jason believed 1000 players in a week would be wonderful. A thousand players joined in the first hour.
Over time, Aurora Feints' game didn't gain traction. They don't make enough money to keep playing.
They could only make enough for one month.
Instead of buying video games, buy technology
Jason saw that they established a leaderboard, chat rooms, and multiplayer capabilities and believed other developers would want to use these.
They opted to sell the prior game's technology.
OpenFeint.
Assisting other game developers
They had no money in the bank to create everything needed to make the technology user-friendly.
Jason and Daniel designed a website saying:
“If you’re making a video game and want to have a drop in multiplayer support, you can use our system”
TechCrunch covered their website launch, and they gained a few hundred mailing list subscribers.
They raised seed funding with the mailing list.
Nearly all iPhone game developers started adopting the Open Feint logo.
“It was pretty wild… It was really like a whole social platform for people to play with their friends.”
What kind of a business model was it?
OpenFeint originally planned to make the software free for all games. As the game gained popularity, they demanded payment.
They later concluded it wasn't a good business concept.
It became free eventually.
Acquired for $104 million
Open Feint's users and employees grew tremendously.
GREE bought OpenFeint for $104 million in April 2011.
GREE initially committed to helping Jason and his team build a fantastic company.
Three or four months after the acquisition, Jason recognized they had a different vision.
He quit.
Jason's Original Vision for the iPad
Jason focused on distribution in 2012 to help businesses stand out.
The iPad market and user base were growing tremendously.
Jason said the iPad may replace mobile gadgets.
iPad gamers behaved differently than mobile gamers.
People sat longer and experienced more using an iPad.
“The idea I had was what if we built a gaming business that was more like traditional video games but played on tablets as opposed to some kind of mobile game that I’ve been doing before.”
Unexpected insight after researching the video game industry
Jason learned from studying the gaming industry that long-standing companies had advantages beyond a single release.
Previously, long-standing video game firms had their own distribution system. This distribution strategy could buffer time between successful titles.
Sony, Microsoft, and Valve all have gaming consoles and online stores.
So he built a distribution system.
He created a group chat app for gamers.
He envisioned a team-based multiplayer game with text and voice interaction.
His objective was to develop a communication network, release more games, and start a game distribution business.
Remaking the video game League of Legends
Jason and his crew reimagined a League of Legends game mode for 12-inch glass.
They adapted the game for tablets.
League of Legends was PC-only.
So they rebuilt it.
They overhauled the game and included native mobile experiences to stand out.
Hammer and Chisel was the company's name.
18 people worked on the game.
The game was funded. The game took 2.5 years to make.
Was the game a success?
July 2014 marked the game's release. The team's hopes were dashed.
Critics initially praised the game.
Initial installation was widespread.
The game failed.
As time passed, the team realized iPad gaming wouldn't increase much and mobile would win.
Jason was given a fresh idea by Stan Vishnevskiy.
Stan Vishnevskiy was a corporate engineer.
He told Jason about his plan to design a communication app without a game.
This concept seeded modern strife.
“The insight that he really had was to put a couple of dots together… we’re seeing our customers communicating around our own game with all these different apps and also ourselves when we’re playing on PC… We should solve that problem directly rather than needing to build a new game…we should start making it on PC.”
So began Discord.
Online socializing with pals was the newest trend.
Jason grew up playing video games with his friends.
He never played outside.
Jason had many great moments playing video games with his closest buddy, wife, and brother.
Discord was about providing a location for you and your group to speak and hang out.
Like a private cafe, bedroom, or living room.
Discord was developed for you and your friends on computers and phones.
You can quickly call your buddies during a game to conduct a conference call. Put the call on speaker and talk while playing.
Discord wanted to give every player a unique experience. Because coordinating across apps was a headache.
The entire team started concentrating on Discord.
Jason decided Hammer and Chisel would focus on their chat app.
Jason didn't want to make a video game.
How Discord attracted the appropriate attention
During the first five months, the entire team worked on the game and got feedback from friends.
This ensures product improvement. As a result, some teammates' buddies started utilizing Discord.
The team knew it would become something, but the result was buggy. App occasionally crashed.
Jason persuaded a gamer friend to write on Reddit about the software.
New people would find Discord. Why not?
Reddit users discovered Discord and 50 started using it frequently.
Discord was launched.
Rejecting the $10 billion acquisition proposal
Discord has increased in recent years.
It sends billions of messages.
Discord's users aren't tracked. They're privacy-focused.
Purchase offer
Covid boosted Discord's user base.
Weekly, billions of messages were transmitted.
Microsoft offered $10 billion for Discord in 2021.
Jason sold Open Feint for $104m in 2011.
This time, he believed in the product so much that he rejected Microsoft's offer.
“I was talking to some people in the team about which way we could go… The good thing was that most of the team wanted to continue building.”
Last time, Discord was valued at $15 billion.
Discord raised money on March 12, 2022.
The $15 billion corporation raised $500 million in 2021.
:max_bytes(150000):strip_icc():gifv():format(webp)/reiff_headshot-5bfc2a60c9e77c00519a70bd.jpg)