More on Economics & Investing

Quant Galore
3 years ago
I created BAW-IV Trading because I was short on money.
More retail traders means faster, more sophisticated, and more successful methods.
Tech specifications
Only requires a laptop and an internet connection.
We'll use OpenBB's research platform for data/analysis.
Pricing and execution on Options-Quant

Background
You don't need to know the arithmetic details to use this method.
Black-Scholes is a popular option pricing model. It's best for pricing European options. European options are only exercisable at expiration, unlike American options. American options are always exercisable.
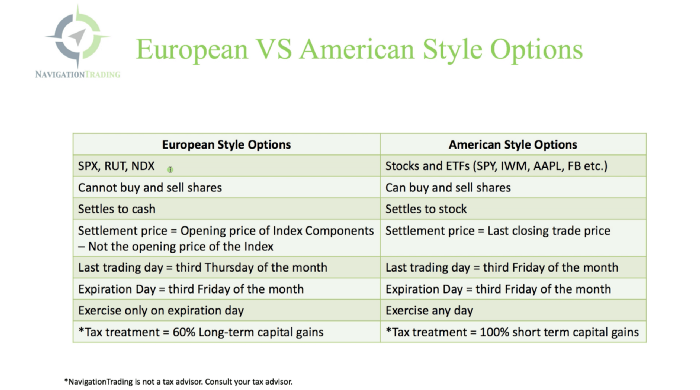
American options carry a premium to cover for the risk of early exercise. The Black-Scholes model doesn't account for this premium, hence it can't price genuine, traded American options.
Barone-Adesi-Whaley (BAW) model. BAW modifies Black-Scholes. It accounts for exercise risk premium and stock dividends. It adds the option's early exercise value to the Black-Scholes value.
The trader need not know the formulaic derivations of this model.
https://ir.nctu.edu.tw/bitstream/11536/14182/1/000264318900005.pdf
Strategy
This strategy targets implied volatility. First, we'll locate liquid options that expire within 30 days and have minimal implied volatility.
After selecting the option that meets the requirements, we price it to get the BAW implied volatility (we choose BAW because it's a more accurate Black-Scholes model). If estimated implied volatility is larger than market volatility, we'll capture the spread.
(Calculated IV — Market IV) = (Profit)
Some approaches to target implied volatility are pricey and inaccessible to individual investors. The best and most cost-effective alternative is to acquire a straddle and delta hedge. This may sound terrifying and pricey, but as shown below, it's much less so.
The Trade
First, we want to find our ideal option, so we use OpenBB terminal to screen for options that:
Have an IV at least 5% lower than the 20-day historical IV
Are no more than 5% out-of-the-money
Expire in less than 30 days
We query:
stocks/options/screen/set low_IV/scr --export Output.csv
This uses the screener function to screen for options that satisfy the above criteria, which we specify in the low IV preset (more on custom presets here). It then saves the matching results to a csv(Excel) file for viewing and analysis.
Stick to liquid names like SPY, AAPL, and QQQ since getting out of a position is just as crucial as getting in. Smaller, illiquid names have higher inefficiencies, which could restrict total profits.

We calculate IV using the BAWbisection model (the bisection is a method of calculating IV, more can be found here.) We price the IV first.

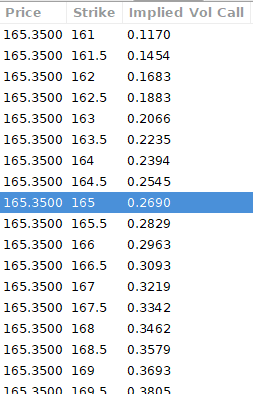
According to the BAW model, implied volatility at this level should be priced at 26.90%. When re-pricing the put, IV is 24.34%, up 3%.
Now it's evident. We must purchase the straddle (long the call and long the put) assuming the computed implied volatility is more appropriate and efficient than the market's. We just want to speculate on volatility, not price fluctuations, thus we delta hedge.
The Fun Starts
We buy both options for $7.65. (x100 multiplier). Initial delta is 2. For every dollar the stock price swings up or down, our position value moves $2.

We want delta to be 0 to avoid price vulnerability. A delta of 0 suggests our position's value won't change from underlying price changes. Being delta-hedged allows us to profit/lose from implied volatility. Shorting 2 shares makes us delta-neutral.

That's delta hedging. (Share price * shares traded) = $330.7 to become delta-neutral. You may have noted that delta is not truly 0.00. This is common since delta-hedging means getting as near to 0 as feasible, since it is rare for deltas to align at 0.00.
Now we're vulnerable to changes in Vega (and Gamma, but given we're dynamically hedging, it's not a big risk), or implied volatility. We wanted to gamble that the position's IV would climb by at least 2%, so we'll maintain it delta-hedged and watch IV.
Because the underlying moves continually, the option's delta moves continuously. A trader can short/long 5 AAPL shares at most. Paper trading lets you practice delta-hedging. Being quick-footed will help with this tactic.
Profit-Closing
As expected, implied volatility rose. By 10 minutes before market closure, the call's implied vol rose to 27% and the put's to 24%. This allowed us to sell the call for $4.95 and the put for $4.35, creating a profit of $165.

You may pull historical data to see how this trade performed. Note the implied volatility and pricing in the final options chain for August 5, 2022 (the position date).

Final Thoughts
Congratulations, that was a doozy. To reiterate, we identified tickers prone to increased implied volatility by screening OpenBB's low IV setting. We double-checked the IV by plugging the price into Options-BAW Quant's model. When volatility was off, we bought a straddle and delta-hedged it. Finally, implied volatility returned to a normal level, and we profited on the spread.
The retail trading space is very quickly catching up to that of institutions. Commissions and fees used to kill this method, but now they cost less than $5. Watching momentum, technical analysis, and now quantitative strategies evolve is intriguing.
I'm not linked with these sites and receive no financial benefit from my writing.
Tell me how your experience goes and how I helped; I love success tales.

Arthur Hayes
3 years ago
Contagion
(The author's opinions should not be used to make investment decisions or as a recommendation to invest.)

The pandemic and social media pseudoscience have made us all epidemiologists, for better or worse. Flattening the curve, social distancing, lockdowns—remember? Some of you may remember R0 (R naught), the number of healthy humans the average COVID-infected person infects. Thankfully, the world has moved on from Greater China's nightmare. Politicians have refocused their talent for misdirection on getting their constituents invested in the war for Russian Reunification or Russian Aggression, depending on your side of the iron curtain.
Humanity battles two fronts. A war against an invisible virus (I know your Commander in Chief might have told you COVID is over, but viruses don't follow election cycles and their economic impacts linger long after the last rapid-test clinic has closed); and an undeclared World War between US/NATO and Eurasia/Russia/China. The fiscal and monetary authorities' current policies aim to mitigate these two conflicts' economic effects.
Since all politicians are short-sighted, they usually print money to solve most problems. Printing money is the easiest and fastest way to solve most problems because it can be done immediately without much discussion. The alternative—long-term restructuring of our global economy—would hurt stakeholders and require an honest discussion about our civilization's state. Both of those requirements are non-starters for our short-sighted political friends, so whether your government practices capitalism, communism, socialism, or fascism, they all turn to printing money-ism to solve all problems.
Free money stimulates demand, so people buy crap. Overbuying shit raises prices. Inflation. Every nation has food, energy, or goods inflation. The once-docile plebes demand action when the latter two subsets of inflation rise rapidly. They will be heard at the polls or in the streets. What would you do to feed your crying hungry child?
Global central banks During the pandemic, the Fed, PBOC, BOJ, ECB, and BOE printed money to aid their governments. They worried about inflation and promised to remove fiat liquidity and tighten monetary conditions.
Imagine Nate Diaz's round-house kick to the face. The financial markets probably felt that way when the US and a few others withdrew fiat wampum. Sovereign debt markets suffered a near-record bond market rout.
The undeclared WW3 is intensifying, with recent gas pipeline attacks. The global economy is already struggling, and credit withdrawal will worsen the situation. The next pandemic, the Yield Curve Control (YCC) virus, is spreading as major central banks backtrack on inflation promises. All central banks eventually fail.
Here's a scorecard.
In order to save its financial system, BOE recently reverted to Quantitative Easing (QE).
BOJ Continuing YCC to save their banking system and enable affordable government borrowing.
ECB printing money to buy weak EU member bonds, but will soon start Quantitative Tightening (QT).
PBOC Restarting the money printer to give banks liquidity to support the falling residential property market.
Fed raising rates and QT-shrinking balance sheet.
80% of the world's biggest central banks are printing money again. Only the Fed has remained steadfast in the face of a financial market bloodbath, determined to end the inflation for which it is at least partially responsible—the culmination of decades of bad economic policies and a world war.
YCC printing is the worst for fiat currency and society. Because it necessitates central banks fixing a multi-trillion-dollar bond market. YCC central banks promise to infinitely expand their balance sheets to keep a certain interest rate metric below an unnatural ceiling. The market always wins, crushing humanity with inflation.
BOJ's YCC policy is longest-standing. The BOE joined them, and my essay this week argues that the ECB will follow. The ECB joining YCC would make 60% of major central banks follow this terrible policy. Since the PBOC is part of the Chinese financial system, the number could be 80%. The Chinese will lend any amount to meet their economic activity goals.
The BOE committed to a 13-week, GBP 65bn bond price-fixing operation. However, BOEs YCC may return. If you lose to the market, you're stuck. Since the BOE has announced that it will buy your Gilt at inflated prices, why would you not sell them all? Market participants taking advantage of this policy will only push the bank further into the hole it dug itself, so I expect the BOE to re-up this program and count them as YCC.
In a few trading days, the BOE went from a bank determined to slay inflation by raising interest rates and QT to buying an unlimited amount of UK Gilts. I expect the ECB to be dragged kicking and screaming into a similar policy. Spoiler alert: big daddy Fed will eventually die from the YCC virus.
Threadneedle St, London EC2R 8AH, UK
Before we discuss the BOE's recent missteps, a chatroom member called the British royal family the Kardashians with Crowns, which made me laugh. I'm sad about royal attention. If the public was as interested in energy and economic policies as they are in how the late Queen treated Meghan, Duchess of Sussex, UK politicians might not have been able to get away with energy and economic fairy tales.
The BOE printed money to recover from COVID, as all good central banks do. For historical context, this chart shows the BOE's total assets as a percentage of GDP since its founding in the 18th century.
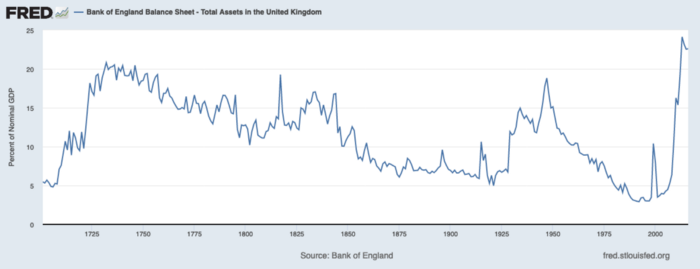
The UK has had a rough three centuries. Pandemics, empire wars, civil wars, world wars. Even so, the BOE's recent money printing was its most aggressive ever!
BOE Total Assets as % of GDP (white) vs. UK CPI
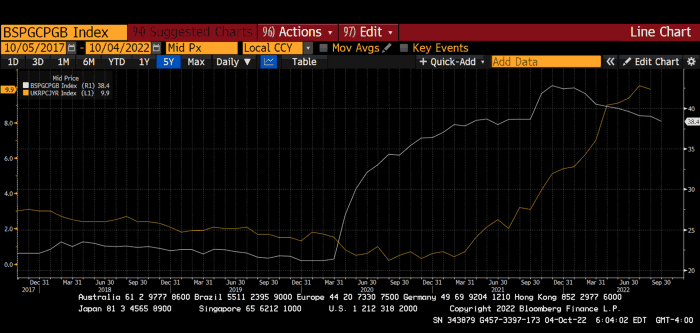
Now, inflation responded slowly to the bank's most aggressive monetary loosening. King Charles wishes the gold line above showed his popularity, but it shows his subjects' suffering.
The BOE recognized early that its money printing caused runaway inflation. In its August 2022 report, the bank predicted that inflation would reach 13% by year end before aggressively tapering in 2023 and 2024.
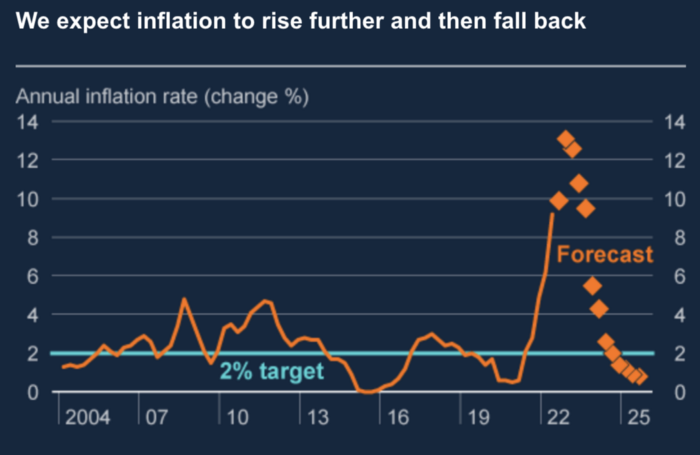
Aug 2022 BOE Monetary Policy Report
The BOE was the first major central bank to reduce its balance sheet and raise its policy rate to help.
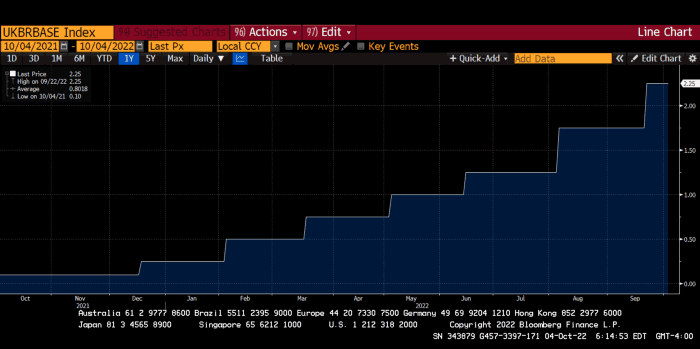
The BOE first raised rates in December 2021. Back then, JayPow wasn't even considering raising rates.
UK policymakers, like most developed nations, believe in energy fairy tales. Namely, that the developed world, which grew in lockstep with hydrocarbon use, could switch to wind and solar by 2050. The UK's energy import bill has grown while coal, North Sea oil, and possibly stranded shale oil have been ignored.
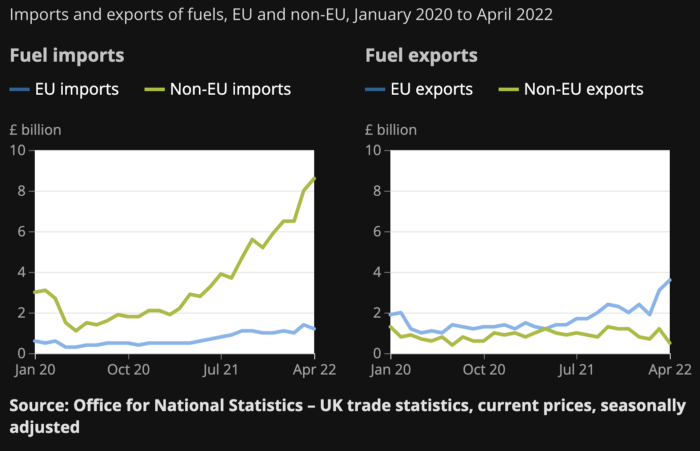
WW3 is an economic war that is balkanizing energy markets, which will continue to inflate. A nation that imports energy and has printed the most money in its history cannot avoid inflation.
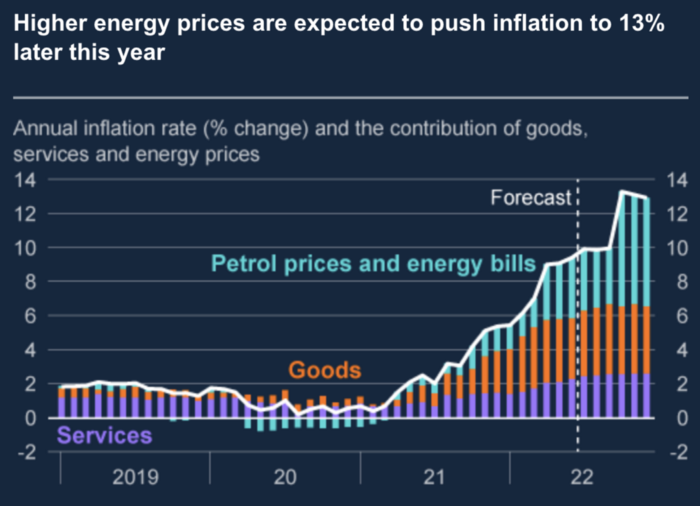
The chart above shows that energy inflation is a major cause of plebe pain.
The UK is hit by a double whammy: the BOE must remove credit to reduce demand, and energy prices must rise due to WW3 inflation. That's not economic growth.
Boris Johnson was knocked out by his country's poor economic performance, not his lockdown at 10 Downing St. Prime Minister Truss and her merry band of fools arrived with the tried-and-true government remedy: goodies for everyone.
She released a budget full of economic stimulants. She cut corporate and individual taxes for the rich. She plans to give poor people vouchers for higher energy bills. Woohoo! Margret Thatcher's new pants suit.
My buddy Jim Bianco said Truss budget's problem is that it works. It will boost activity at a time when inflation is over 10%. Truss' budget didn't include austerity measures like tax increases or spending cuts, which the bond market wanted. The bond market protested.
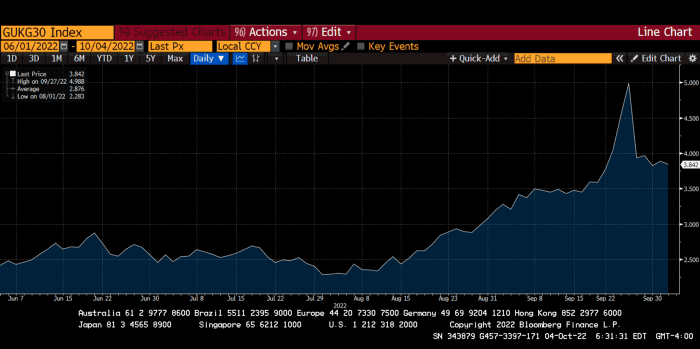
30-year Gilt yield chart. Yields spiked the most ever after Truss announced her budget, as shown. The Gilt market is the longest-running bond market in the world.
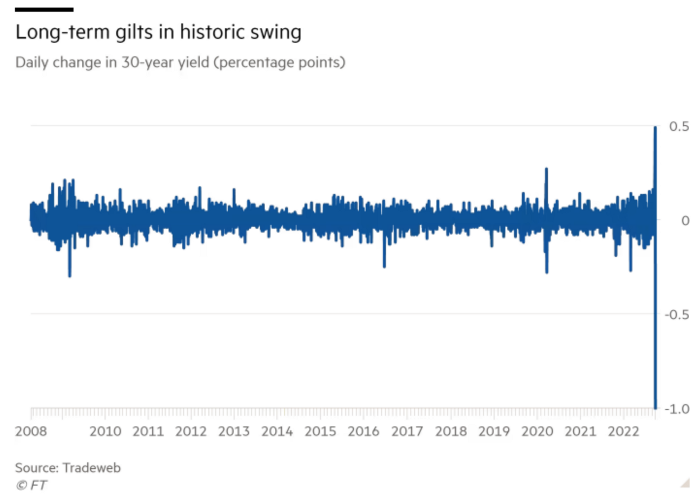
The Gilt market showed the pole who's boss with Cardi B.
Before this, the BOE was super-committed to fighting inflation. To their credit, they raised short-term rates and shrank their balance sheet. However, rapid yield rises threatened to destroy the entire highly leveraged UK financial system overnight, forcing them to change course.
Accounting gimmicks allowed by regulators for pension funds posed a systemic threat to the UK banking system. UK pension funds could use interest rate market levered derivatives to match liabilities. When rates rise, short rate derivatives require more margin. The pension funds spent all their money trying to pick stonks and whatever else their sell side banker could stuff them with, so the historic rate spike would have bankrupted them overnight. The FT describes BOE-supervised chicanery well.
To avoid a financial apocalypse, the BOE in one morning abandoned all their hard work and started buying unlimited long-dated Gilts to drive prices down.
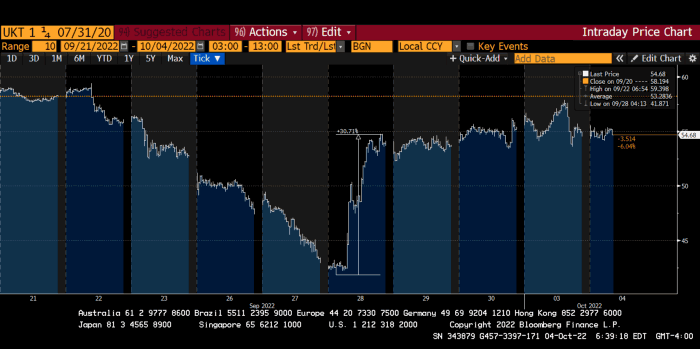
Another reminder to never fight a central bank. The 30-year Gilt is shown above. After the BOE restarted the money printer on September 28, this bond rose 30%. Thirty-fucking-percent! Developed market sovereign bonds rarely move daily. You're invested in His Majesty's government obligations, not a Chinese property developer's offshore USD bond.
The political need to give people goodies to help them fight the terrible economy ran into a financial reality. The central bank protected the UK financial system from asset-price deflation because, like all modern economies, it is debt-based and highly levered. As bad as it is, inflation is not their top priority. The BOE example demonstrated that. To save the financial system, they abandoned almost a year of prudent monetary policy in a few hours. They also started the endgame.
Let's play Central Bankers Say the Darndest Things before we go to the continent (and sorry if you live on a continent other than Europe, but you're not culturally relevant).
Pre-meltdown BOE output:
FT, October 17, 2021 On Sunday, the Bank of England governor warned that it must act to curb inflationary pressure, ignoring financial market moves that have priced in the first interest rate increase before the end of the year.
On July 19, 2022, Gov. Andrew Bailey spoke. Our 2% inflation target is unwavering. We'll do our job.
August 4th 2022 MPC monetary policy announcement According to its mandate, the MPC will sustainably return inflation to 2% in the medium term.
Catherine Mann, MPC member, September 5, 2022 speech. Fast and forceful monetary tightening, possibly followed by a hold or reversal, is better than gradualism because it promotes inflation expectations' role in bringing inflation back to 2% over the medium term.
When their financial system nearly collapsed in one trading session, they said:
The Bank of England's Financial Policy Committee warned on 28 September that gilt market dysfunction threatened UK financial stability. It advised action and supported the Bank's urgent gilt market purchases for financial stability.
It works when the price goes up but not down. Is my crypto portfolio dysfunctional enough to get a BOE bailout?
Next, the EU and ECB. The ECB is also fighting inflation, but it will also succumb to the YCC virus for the same reasons as the BOE.
Frankfurt am Main, ECB Tower, Sonnemannstraße 20, 60314
Only France and Germany matter economically in the EU. Modern European history has focused on keeping Germany and Russia apart. German manufacturing and cheap Russian goods could change geopolitics.
France created the EU to keep Germany down, and the Germans only cooperated because of WWII guilt. France's interests are shared by the US, which lurks in the shadows to prevent a Germany-Russia alliance. A weak EU benefits US politics. Avoid unification of Eurasia. (I paraphrased daddy Felix because I thought quoting a large part of his most recent missive would get me spanked.)
As with everything, understanding Germany's energy policy is the best way to understand why the German economy is fundamentally fucked and why that spells doom for the EU. Germany, the EU's main economic engine, is being crippled by high energy prices, threatening a depression. This economic downturn threatens the union. The ECB may have to abandon plans to shrink its balance sheet and switch to YCC to save the EU's unholy political union.
France did the smart thing and went all in on nuclear energy, which is rare in geopolitics. 70% of electricity is nuclear-powered. Their manufacturing base can survive Russian gas cuts. Germany cannot.
My boy Zoltan made this great graphic showing how screwed Germany is as cheap Russian gas leaves the industrial economy.
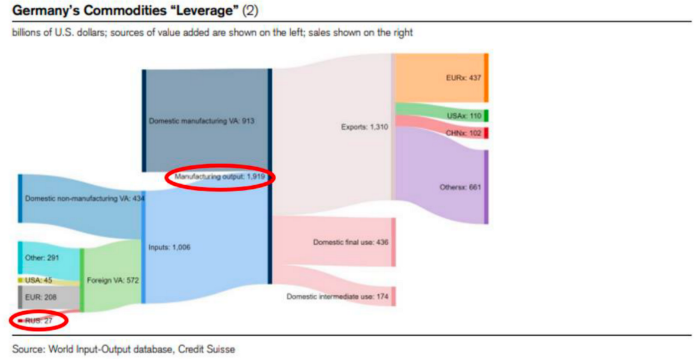
$27 billion of Russian gas powers almost $2 trillion of German economic output, a 75x energy leverage. The German public was duped into believing the same energy fairy tales as their politicians, and they overwhelmingly allowed the Green party to dismantle any efforts to build a nuclear energy ecosystem over the past several decades. Germany, unlike France, must import expensive American and Qatari LNG via supertankers due to Nordstream I and II pipeline sabotage.
American gas exports to Europe are touted by the media. Gas is cheap because America isn't the Western world's swing producer. If gas prices rise domestically in America, the plebes would demand the end of imports to avoid paying more to heat their homes.
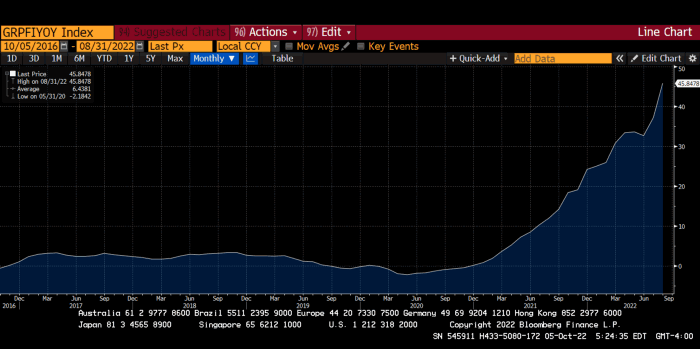
German goods would cost much more in this scenario. German producer prices rose 46% YoY in August. The German current account is rapidly approaching zero and will soon be negative.
German PPI Change YoY
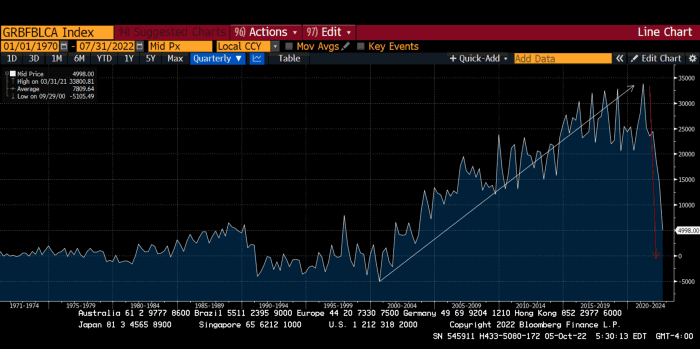
German Current Account
The reason this matters is a curious construction called TARGET2. Let’s hear from the horse’s mouth what exactly this beat is:
TARGET2 is the real-time gross settlement (RTGS) system owned and operated by the Eurosystem. Central banks and commercial banks can submit payment orders in euro to TARGET2, where they are processed and settled in central bank money, i.e. money held in an account with a central bank.
Source: ECB
Let me explain this in plain English for those unfamiliar with economic dogma.
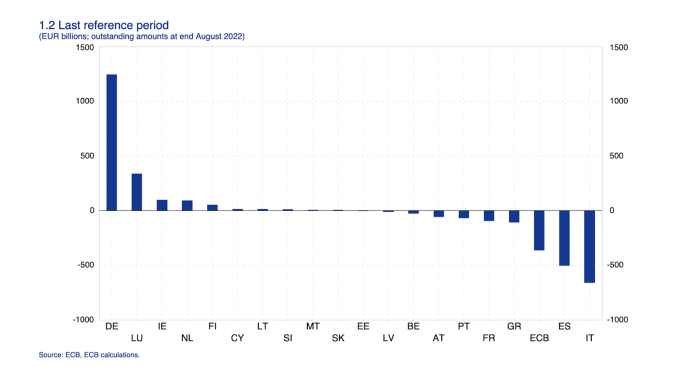
This chart shows intra-EU credits and debits. TARGET2. Germany, Europe's powerhouse, is owed money. IOU-buying Greeks buy G-wagons. The G-wagon pickup truck is badass.

If all EU countries had fiat currencies, the Deutsche Mark would be stronger than the Italian Lira, according to the chart above. If Europe had to buy goods from non-EU countries, the Euro would be much weaker. Credits and debits between smaller political units smooth out imbalances in other federal-provincial-state political systems. Financial and fiscal unions allow this. The EU is financial, so the centre cannot force the periphery to settle their imbalances.
Greece has never had to buy Fords or Kias instead of BMWs, but what if Germany had to shut down its auto manufacturing plants due to energy shortages?
Italians have done well buying ammonia from Germany rather than China, but what if BASF had to close its Ludwigshafen facility due to a lack of affordable natural gas?
I think you're seeing the issue.
Instead of Germany, EU countries would owe foreign producers like America, China, South Korea, Japan, etc. Since these countries aren't tied into an uneconomic union for politics, they'll demand hard fiat currency like USD instead of Euros, which have become toilet paper (or toilet plastic).
Keynesian economists have a simple solution for politicians who can't afford market prices. Government debt can maintain production. The debt covers the difference between what a business can afford and the international energy market price.
Germans are monetary policy conservative because of the Weimar Republic's hyperinflation. The Bundesbank is the only thing preventing ECB profligacy. Germany must print its way out without cheap energy. Like other nations, they will issue more bonds for fiscal transfers.
More Bunds mean lower prices. Without German monetary discipline, the Euro would have become a trash currency like any other emerging market that imports energy and food and has uncompetitive labor.
Bunds price all EU country bonds. The ECB's money printing is designed to keep the spread of weak EU member bonds vs. Bunds low. Everyone falls with Bunds.
Like the UK, German politicians seeking re-election will likely cause a Bunds selloff. Bond investors will understandably reject their promises of goodies for industry and individuals to offset the lack of cheap Russian gas. Long-dated Bunds will be smoked like UK Gilts. The ECB will face a wave of ultra-levered financial players who will go bankrupt if they mark to market their fixed income derivatives books at higher Bund yields.
Some treats People: Germany will spend 200B to help consumers and businesses cope with energy prices, including promoting renewable energy.
That, ladies and germs, is why the ECB will immediately abandon QT, move to a stop-gap QE program to normalize the Bund and every other EU bond market, and eventually graduate to YCC as the market vomits bonds of all stripes into Christine Lagarde's loving hands. She probably has soft hands.
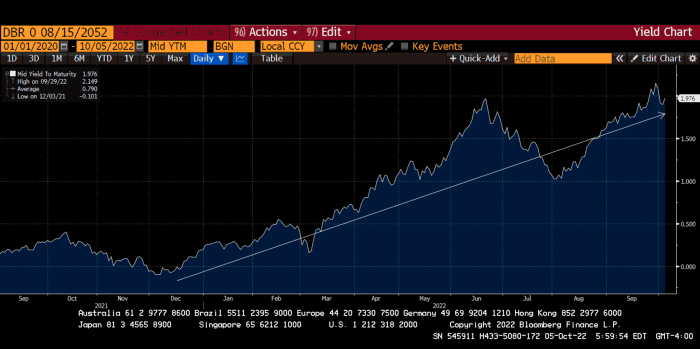
The 30-year Bund market has noticed Germany's economic collapse. 2021 yields skyrocketed.
30-year Bund Yield
ECB Says the Darndest Things:
Because inflation is too high and likely to stay above our target for a long time, we took today's decision and expect to raise interest rates further.- Christine Lagarde, ECB Press Conference, Sept 8.
The Governing Council will adjust all of its instruments to stabilize inflation at 2% over the medium term. July 21 ECB Monetary Decision
Everyone struggles with high inflation. The Governing Council will ensure medium-term inflation returns to two percent. June 9th ECB Press Conference
I'm excited to read the after. Like the BOE, the ECB may abandon their plans to shrink their balance sheet and resume QE due to debt market dysfunction.
Eighty Percent
I like YCC like dark chocolate over 80%. ;).
Can 80% of the world's major central banks' QE and/or YCC overcome Sir Powell's toughness on fungible risky asset prices?
Gold and crypto are fungible global risky assets. Satoshis and gold bars are the same in New York, London, Frankfurt, Tokyo, and Shanghai.
As more Euros, Yen, Renminbi, and Pounds are printed, people will move their savings into Dollars or other stores of value. As the Fed raises rates and reduces its balance sheet, the USD will strengthen. Gold/EUR and BTC/JPY may also attract buyers.
Gold and crypto markets are much smaller than the trillions in fiat money that will be printed, so they will appreciate in non-USD currencies. These flows only matter in one instance because we trade the global or USD price. Arbitrage occurs when BTC/EUR rises faster than EUR/USD. Here is how it works:
An investor based in the USD notices that BTC is expensive in EUR terms.
Instead of buying BTC, this investor borrows USD and then sells it.
After that, they sell BTC and buy EUR.
Then they choose to sell EUR and buy USD.
The investor receives their profit after repaying the USD loan.
This triangular FX arbitrage will align the global/USD BTC price with the elevated EUR, JPY, CNY, and GBP prices.
Even if the Fed continues QT, which I doubt they can do past early 2023, small stores of value like gold and Bitcoin may rise as non-Fed central banks get serious about printing money.
“Arthur, this is just more copium,” you might retort.
Patience. This takes time. Economic and political forcing functions take time. The BOE example shows that bond markets will reject politicians' policies to appease voters. Decades of bad energy policy have no immediate fix. Money printing is the only politically viable option. Bond yields will rise as bond markets see more stimulative budgets, and the over-leveraged fiat debt-based financial system will collapse quickly, followed by a monetary bailout.
America has enough food, fuel, and people. China, Europe, Japan, and the UK suffer. America can be autonomous. Thus, the Fed can prioritize domestic political inflation concerns over supplying the world (and most of its allies) with dollars. A steady flow of dollars allows other nations to print their currencies and buy energy in USD. If the strongest player wins, everyone else loses.
I'm making a GDP-weighted index of these five central banks' money printing. When ready, I'll share its rate of change. This will show when the 80%'s money printing exceeds the Fed's tightening.

Justin Kuepper
3 years ago
Day Trading Introduction
Historically, only large financial institutions, brokerages, and trading houses could actively trade in the stock market. With instant global news dissemination and low commissions, developments such as discount brokerages and online trading have leveled the playing—or should we say trading—field. It's never been easier for retail investors to trade like pros thanks to trading platforms like Robinhood and zero commissions.
Day trading is a lucrative career (as long as you do it properly). But it can be difficult for newbies, especially if they aren't fully prepared with a strategy. Even the most experienced day traders can lose money.
So, how does day trading work?
Day Trading Basics
Day trading is the practice of buying and selling a security on the same trading day. It occurs in all markets, but is most common in forex and stock markets. Day traders are typically well educated and well funded. For small price movements in highly liquid stocks or currencies, they use leverage and short-term trading strategies.
Day traders are tuned into short-term market events. News trading is a popular strategy. Scheduled announcements like economic data, corporate earnings, or interest rates are influenced by market psychology. Markets react when expectations are not met or exceeded, usually with large moves, which can help day traders.
Intraday trading strategies abound. Among these are:
- Scalping: This strategy seeks to profit from minor price changes throughout the day.
- Range trading: To determine buy and sell levels, range traders use support and resistance levels.
- News-based trading exploits the increased volatility around news events.
- High-frequency trading (HFT): The use of sophisticated algorithms to exploit small or short-term market inefficiencies.
A Disputed Practice
Day trading's profit potential is often debated on Wall Street. Scammers have enticed novices by promising huge returns in a short time. Sadly, the notion that trading is a get-rich-quick scheme persists. Some daytrade without knowledge. But some day traders succeed despite—or perhaps because of—the risks.
Day trading is frowned upon by many professional money managers. They claim that the reward rarely outweighs the risk. Those who day trade, however, claim there are profits to be made. Profitable day trading is possible, but it is risky and requires considerable skill. Moreover, economists and financial professionals agree that active trading strategies tend to underperform passive index strategies over time, especially when fees and taxes are factored in.
Day trading is not for everyone and is risky. It also requires a thorough understanding of how markets work and various short-term profit strategies. Though day traders' success stories often get a lot of media attention, keep in mind that most day traders are not wealthy: Many will fail, while others will barely survive. Also, while skill is important, bad luck can sink even the most experienced day trader.
Characteristics of a Day Trader
Experts in the field are typically well-established professional day traders.
They usually have extensive market knowledge. Here are some prerequisites for successful day trading.
Market knowledge and experience
Those who try to day-trade without understanding market fundamentals frequently lose. Day traders should be able to perform technical analysis and read charts. Charts can be misleading if not fully understood. Do your homework and know the ins and outs of the products you trade.
Enough capital
Day traders only use risk capital they can lose. This not only saves them money but also helps them trade without emotion. To profit from intraday price movements, a lot of capital is often required. Most day traders use high levels of leverage in margin accounts, and volatile market swings can trigger large margin calls on short notice.
Strategy
A trader needs a competitive advantage. Swing trading, arbitrage, and trading news are all common day trading strategies. They tweak these strategies until they consistently profit and limit losses.
Strategy Breakdown:
Type | Risk | Reward
Swing Trading | High | High
Arbitrage | Low | Medium
Trading News | Medium | Medium
Mergers/Acquisitions | Medium | High
Discipline
A profitable strategy is useless without discipline. Many day traders lose money because they don't meet their own criteria. “Plan the trade and trade the plan,” they say. Success requires discipline.
Day traders profit from market volatility. For a day trader, a stock's daily movement is appealing. This could be due to an earnings report, investor sentiment, or even general economic or company news.
Day traders also prefer highly liquid stocks because they can change positions without affecting the stock's price. Traders may buy a stock if the price rises. If the price falls, a trader may decide to sell short to profit.
A day trader wants to trade a stock that moves (a lot).
Day Trading for a Living
Professional day traders can be self-employed or employed by a larger institution.
Most day traders work for large firms like hedge funds and banks' proprietary trading desks. These traders benefit from direct counterparty lines, a trading desk, large capital and leverage, and expensive analytical software (among other advantages). By taking advantage of arbitrage and news events, these traders can profit from less risky day trades before individual traders react.
Individual traders often manage other people’s money or simply trade with their own. They rarely have access to a trading desk, but they frequently have strong ties to a brokerage (due to high commissions) and other resources. However, their limited scope prevents them from directly competing with institutional day traders. Not to mention more risks. Individuals typically day trade highly liquid stocks using technical analysis and swing trades, with some leverage.
Day trading necessitates access to some of the most complex financial products and services. Day traders usually need:
Access to a trading desk
Traders who work for large institutions or manage large sums of money usually use this. The trading or dealing desk provides these traders with immediate order execution, which is critical during volatile market conditions. For example, when an acquisition is announced, day traders interested in merger arbitrage can place orders before the rest of the market.
News sources
The majority of day trading opportunities come from news, so being the first to know when something significant happens is critical. It has access to multiple leading newswires, constant news coverage, and software that continuously analyzes news sources for important stories.
Analytical tools
Most day traders rely on expensive trading software. Technical traders and swing traders rely on software more than news. This software's features include:
-
Automatic pattern recognition: It can identify technical indicators like flags and channels, or more complex indicators like Elliott Wave patterns.
-
Genetic and neural applications: These programs use neural networks and genetic algorithms to improve trading systems and make more accurate price predictions.
-
Broker integration: Some of these apps even connect directly to the brokerage, allowing for instant and even automatic trade execution. This reduces trading emotion and improves execution times.
-
Backtesting: This allows traders to look at past performance of a strategy to predict future performance. Remember that past results do not always predict future results.
Together, these tools give traders a competitive advantage. It's easy to see why inexperienced traders lose money without them. A day trader's earnings potential is also affected by the market in which they trade, their capital, and their time commitment.
Day Trading Risks
Day trading can be intimidating for the average investor due to the numerous risks involved. The SEC highlights the following risks of day trading:
Because day traders typically lose money in their first months of trading and many never make profits, they should only risk money they can afford to lose.
Trading is a full-time job that is stressful and costly: Observing dozens of ticker quotes and price fluctuations to spot market trends requires intense concentration. Day traders also spend a lot on commissions, training, and computers.
Day traders heavily rely on borrowing: Day-trading strategies rely on borrowed funds to make profits, which is why many day traders lose everything and end up in debt.
Avoid easy profit promises: Avoid “hot tips” and “expert advice” from day trading newsletters and websites, and be wary of day trading educational seminars and classes.
Should You Day Trade?
As stated previously, day trading as a career can be difficult and demanding.
- First, you must be familiar with the trading world and know your risk tolerance, capital, and goals.
- Day trading also takes a lot of time. You'll need to put in a lot of time if you want to perfect your strategies and make money. Part-time or whenever isn't going to cut it. You must be fully committed.
- If you decide trading is for you, remember to start small. Concentrate on a few stocks rather than jumping into the market blindly. Enlarging your trading strategy can result in big losses.
- Finally, keep your cool and avoid trading emotionally. The more you can do that, the better. Keeping a level head allows you to stay focused and on track.
If you follow these simple rules, you may be on your way to a successful day trading career.
Is Day Trading Illegal?
Day trading is not illegal or unethical, but it is risky. Because most day-trading strategies use margin accounts, day traders risk losing more than they invest and becoming heavily in debt.
How Can Arbitrage Be Used in Day Trading?
Arbitrage is the simultaneous purchase and sale of a security in multiple markets to profit from small price differences. Because arbitrage ensures that any deviation in an asset's price from its fair value is quickly corrected, arbitrage opportunities are rare.
Why Don’t Day Traders Hold Positions Overnight?
Day traders rarely hold overnight positions for several reasons: Overnight trades require more capital because most brokers require higher margin; stocks can gap up or down on overnight news, causing big trading losses; and holding a losing position overnight in the hope of recovering some or all of the losses may be against the trader's core day-trading philosophy.
What Are Day Trader Margin Requirements?
Regulation D requires that a pattern day trader client of a broker-dealer maintain at all times $25,000 in equity in their account.
How Much Buying Power Does Day Trading Have?
Buying power is the total amount of funds an investor has available to trade securities. FINRA rules allow a pattern day trader to trade up to four times their maintenance margin excess as of the previous day's close.
The Verdict
Although controversial, day trading can be a profitable strategy. Day traders, both institutional and retail, keep the markets efficient and liquid. Though day trading is still popular among novice traders, it should be left to those with the necessary skills and resources.
You might also like

obimy.app
3 years ago
How TikTok helped us grow to 6 million users
This resulted to obimy's new audience.

Hi! obimy's official account. Here, we'll teach app developers and marketers. In 2022, our downloads increased dramatically, so we'll share what we learned.
obimy is what we call a ‘senseger’. It's a new method to communicate digitally. Instead of text, obimy users connect through senses and moods. Feeling playful? Flirt with your partner, pat a pal, or dump water on a classmate. Each feeling is an interactive animation with vibration. It's a wordless app. App Store and Google Play have obimy.
We had 20,000 users in 2022. Two to five thousand of them opened the app monthly. Our DAU metric was 500.
We have 6 million users after 6 months. 500,000 individuals use obimy daily. obimy was the top lifestyle app this week in the U.S.
And TikTok helped.
TikTok fuels obimys' growth. It's why our app exploded. How and what did we learn? Our Head of Marketing, Anastasia Avramenko, knows.
our actions prior to TikTok
We wanted to achieve product-market fit through organic expansion. Quora, Reddit, Facebook Groups, Facebook Ads, Google Ads, Apple Search Ads, and social media activity were tested. Nothing worked. Our CPI was sometimes $4, so unit economics didn't work.
We studied our markets and made audience hypotheses. We promoted our goods and studied our audience through social media quizzes. Our target demographic was Americans in long-distance relationships. I designed quizzes like Test the Strength of Your Relationship to better understand the user base. After each quiz, we encouraged users to download the app to enhance their connection and bridge the distance.
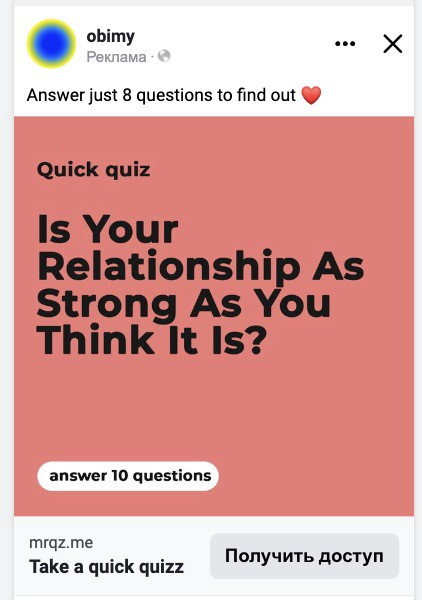
We got 1,000 responses for $50. This helped us comprehend the audience's grief and coping strategies (aka our rivals). I based action items on answers given. If you can't embrace a loved one, use obimy.
We also tried Facebook and Google ads. From the start, we knew it wouldn't work.
We were desperate to discover a free way to get more users.
Our journey to TikTok
TikTok is a great venue for emerging creators. It also helped reach people. Before obimy, my TikTok videos garnered 12 million views without sponsored promotion.
We had to act. TikTok was required.

I wasn't a TikTok user before obimy. Initially, I uploaded promotional content. Call-to-actions appear strange next to dancing challenges and my money don't jiggle jiggle. I learned TikTok. Watch TikTok for an hour was on my to-do list. What a dream job!
Our most popular movies presented the app alongside text outlining what it does. We started promoting them in Europe and the U.S. and got a 16% CTR and $1 CPI, an improvement over our previous efforts.
Somehow, we were expanding. So we came up with new hypotheses, calls to action, and content.
Four months passed, yet we saw no organic growth.
Russia attacked Ukraine.
Our app aimed to be helpful. For now, we're focusing on our Ukrainian audience. I posted sloppy TikToks illustrating how obimy can help during shelling or air raids.
In two hours, Kostia sent me our visitor count. Our servers crashed.
Initially, we had several thousand daily users. Over 200,000 users joined obimy in a week. They posted obimy videos on TikTok, drawing additional users. We've also resumed U.S. video promotion.
We gained 2,000,000 new members with less than $100 in ads, primarily in the U.S. and U.K.
TikTok helped.
The figures
We were confident we'd chosen the ideal tool for organic growth.
Over 45 million people have viewed our own videos plus a ton of user-generated content with the hashtag #obimy.
About 375 thousand people have liked all of our individual videos.
The number of downloads and the virality of videos are directly correlated.
Where are we now?
TikTok fuels our organic growth. We post 56 videos every week and pay to promote viral content.
We use UGC and influencers. We worked with Universal Music Italy on Eurovision. They offered to promote us through their million-follower TikTok influencers. We thought their followers would improve our audience, but it didn't matter. Integration didn't help us. Users that share obimy videos with their followers can reach several million views, which affects our download rate.
After the dust settled, we determined our key audience was 13-18-year-olds. They want to express themselves, but it's sometimes difficult. We're searching for methods to better engage with our users. We opened a Discord server to discuss anime and video games and gather app and content feedback.
TikTok helps us test product updates and hypotheses. Example: I once thought we might raise MAU by prompting users to add strangers as friends. Instead of asking our team to construct it, I made a TikTok urging users to share invite URLs. Users share links under every video we upload, embracing people worldwide.
Key lessons
Don't direct-sell. TikTok isn't for Instagram, Facebook, or YouTube promo videos. Conventional advertisements don't fit. Most users will swipe up and watch humorous doggos.
More product videos are better. Finally. So what?
Encourage interaction. Tagging friends in comments or making videos with the app promotes it more than any marketing spend.
Be odd and risqué. A user mistakenly sent a French kiss to their mom in one of our most popular videos.
TikTok helps test hypotheses and build your user base. It also helps develop apps. In our upcoming blog, we'll guide you through obimy's design revisions based on TikTok. Follow us on Twitter, Instagram, and TikTok.
Dmytro Spilka
3 years ago
Why NFTs Have a Bright Future Away from Collectible Art After Punks and Apes

After a crazy second half of 2021 and significant trade volumes into 2022, the market for NFT artworks like Bored Ape Yacht Club, CryptoPunks, and Pudgy Penguins has begun a sharp collapse as market downturns hit token values.
DappRadar data shows NFT monthly sales have fallen below $1 billion since June 2021. OpenSea, the world's largest NFT exchange, has seen sales volume decline 75% since May and is trading like July 2021.
Prices of popular non-fungible tokens have also decreased. Bored Ape Yacht Club (BAYC) has witnessed volume and sales drop 63% and 15%, respectively, in the past month.
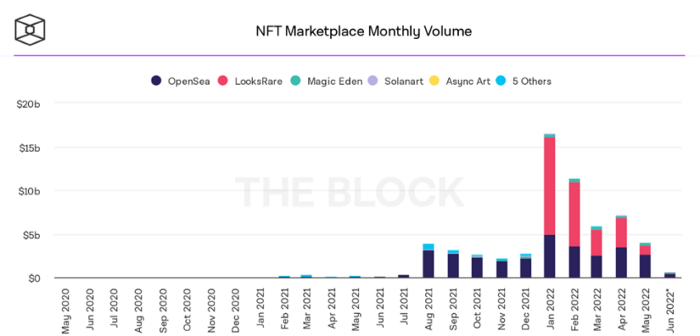
BeInCrypto analysis shows market decline. May 2022 cryptocurrency marketplace volume was $4 billion, according to a news platform. This is a sharp drop from April's $7.18 billion.
OpenSea, a big marketplace, contributed $2.6 billion, while LooksRare, Magic Eden, and Solanart also contributed.
NFT markets are digital platforms for buying and selling tokens, similar stock trading platforms. Although some of the world's largest exchanges offer NFT wallets, most users store their NFTs on their favorite marketplaces.
In January 2022, overall NFT sales volume was $16.57 billion, with LooksRare contributing $11.1 billion. May 2022's volume was $12.57 less than January, a 75% drop, and June's is expected to be considerably smaller.
A World Based on Utility
Despite declines in NFT trading volumes, not all investors are negative on NFTs. Although there are uncertainties about the sustainability of NFT-based art collections, there are fewer reservations about utility-based tokens and their significance in technology's future.
In June, business CEO Christof Straub said NFTs may help artists monetize unreleased content, resuscitate catalogs, establish deeper fan connections, and make processes more efficient through technology.
We all know NFTs can't be JPEGs. Straub noted that NFT music rights can offer more equitable rewards to musicians.
Music NFTs are here to stay if they have real value, solve real problems, are trusted and lawful, and have fair and sustainable business models.
NFTs can transform numerous industries, including music. Market opinion is shifting towards tokens with more utility than the social media artworks we're used to seeing.
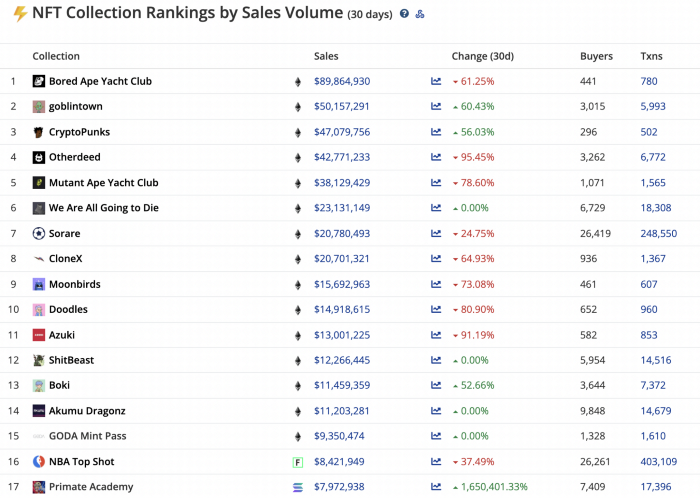
While the major NFT names remain dominant in terms of volume, new utility-based initiatives are emerging as top 20 collections.
Otherdeed, Sorare, and NBA Top Shot are NFT-based games that rank above Bored Ape Yacht Club and Cryptopunks.
Users can switch video NFTs of basketball players in NBA Top Shot. Similar efforts are emerging in the non-fungible landscape.
Sorare shows how NFTs can support a new way of playing fantasy football, where participants buy and swap trading cards to create a 5-player team that wins rewards based on real-life performances.
Sorare raised 579.7 million in one of Europe's largest Series B financing deals in September 2021. Recently, the platform revealed plans to expand into Major League Baseball.
Strong growth indications suggest a promising future for NFTs. The value of art-based collections like BAYC and CryptoPunks may be questioned as markets become diluted by new limited collections, but the potential for NFTs to become intrinsically linked to tangible utility like online gaming, music and art, and even corporate reward schemes shows the industry has a bright future.

DC Palter
2 years ago
Why Are There So Few Startups in Japan?
Japan's startup challenge: 7 reasons

Every day, another Silicon Valley business is bought for a billion dollars, making its founders rich while growing the economy and improving consumers' lives.
Google, Amazon, Twitter, and Medium dominate our daily lives. Tesla automobiles and Moderna Covid vaccinations.
The startup movement started in Silicon Valley, California, but the rest of the world is catching up. Global startup buzz is rising. Except Japan.
644 of CB Insights' 1170 unicorns—successful firms valued at over $1 billion—are US-based. China follows with 302 and India third with 108.
Japan? 6!
1% of US startups succeed. The third-largest economy is tied with small Switzerland for startup success.
Mexico (8), Indonesia (12), and Brazil (12) have more successful startups than Japan (16). South Korea has 16. Yikes! Problem?
Why Don't Startups Exist in Japan More?
Not about money. Japanese firms invest in startups. To invest in startups, big Japanese firms create Silicon Valley offices instead of Tokyo.
Startups aren't the issue either. Local governments are competing to be Japan's Shirikon Tani, providing entrepreneurs financing, office space, and founder visas.
Startup accelerators like Plug and Play in Tokyo, Osaka, and Kyoto, the Startup Hub in Kobe, and Google for Startups are many.
Most of the companies I've encountered in Japan are either local offices of foreign firms aiming to expand into the Japanese market or small businesses offering local services rather than disrupting a staid industry with new ideas.
There must be a reason Japan can develop world-beating giant corporations like Toyota, Nintendo, Shiseido, and Suntory but not inventive startups.
Culture, obviously. Japanese culture excels in teamwork, craftsmanship, and quality, but it hates moving fast, making mistakes, and breaking things.
If you have a brilliant idea in Silicon Valley, quit your job, get money from friends and family, and build a prototype. To fund the business, you approach angel investors and VCs.
Most non-startup folks don't aware that venture capitalists don't want good, profitable enterprises. That's wonderful if you're developing a solid small business to consult, open shops, or make a specialty product. However, you must pay for it or borrow money. Venture capitalists want moon rockets. Silicon Valley is big or bust. Almost 90% will explode and crash. The few successes are remarkable enough to make up for the failures.
Silicon Valley's high-risk, high-reward attitude contrasts with Japan's incrementalism. Japan makes the best automobiles and cleanrooms, but it fails to produce new items that grow the economy.
Changeable? Absolutely. But, what makes huge manufacturing enterprises successful and what makes Japan a safe and comfortable place to live are inextricably connected with the lack of startups.
Barriers to Startup Development in Japan
These are the 7 biggest obstacles to Japanese startup success.
Unresponsive Employment Market
While the lifelong employment system in Japan is evolving, the average employee stays at their firm for 12 years (15 years for men at large organizations) compared to 4.3 years in the US. Seniority, not experience or aptitude, determines career routes, making it tough to quit a job to join a startup and then return to corporate work if it fails.
Conservative Buyers
Even if your product is buggy and undocumented, US customers will migrate to a cheaper, superior one. Japanese corporations demand perfection from their trusted suppliers and keep with them forever. Startups need income fast, yet product evaluation takes forever.
Failure intolerance
Japanese business failures harm lives. Failed forever. It hinders risk-taking. Silicon Valley embraces failure. Build another startup if your first fails. Build a third if that fails. Every setback is viewed as a learning opportunity for success.
4. No Corporate Purchases
Silicon Valley industrial giants will buy fast-growing startups for a lot of money. Many huge firms have stopped developing new goods and instead buy startups after the product is validated.
Japanese companies prefer in-house product development over startup acquisitions. No acquisitions mean no startup investment and no investor reward.
Startup investments can also be monetized through stock market listings. Public stock listings in Japan are risky because the Nikkei was stagnant for 35 years while the S&P rose 14x.
5. Social Unity Above Wealth
In Silicon Valley, everyone wants to be rich. That creates a competitive environment where everyone wants to succeed, but it also promotes fraud and societal problems.
Japan values communal harmony above individual success. Wealthy folks and overachievers are avoided. In Japan, renegades are nearly impossible.
6. Rote Learning Education System
Japanese high school graduates outperform most Americans. Nonetheless, Japanese education is known for its rote memorization. The American system, which fails too many kids, emphasizes creativity to create new products.
Immigration.
Immigrants start 55% of successful Silicon Valley firms. Some come for university, some to escape poverty and war, and some are recruited by Silicon Valley startups and stay to start their own.
Japan is difficult for immigrants to start a business due to language barriers, visa restrictions, and social isolation.
How Japan Can Promote Innovation
Patchwork solutions to deep-rooted cultural issues will not work. If customers don't buy things, immigration visas won't aid startups. Startups must have a chance of being acquired for a huge sum to attract investors. If risky startups fail, employees won't join.
Will Japan never have a startup culture?
Once a consensus is reached, Japan changes rapidly. A dwindling population and standard of living may lead to such consensus.
Toyota and Sony were firms with renowned founders who used technology to transform the world. Repeatable.
Silicon Valley is flawed too. Many people struggle due to wealth disparities, job churn and layoffs, and the tremendous ups and downs of the economy caused by stock market fluctuations.
The founders of the 10% successful startups are heroes. The 90% that fail and return to good-paying jobs with benefits are never mentioned.
Silicon Valley startup culture and Japanese corporate culture are opposites. Each have pros and cons. Big Japanese corporations make the most reliable, dependable, high-quality products yet move too slowly. That's good for creating cars, not social networking apps.
Can innovation and success be encouraged without eroding social cohesion? That can motivate software firms to move fast and break things while recognizing the beauty and precision of expert craftsmen? A hybrid culture where Japan can make the world's best and most original items. Hopefully.
