More on Web3 & Crypto

CyberPunkMetalHead
3 years ago
I talked to ChatGPT about the adoption of cryptocurrencies.

OpenAI's ChatGPT is an amazing AI-powered chatbot. It can write poetry, fiction, and marketing ideas. I was impressed how well ChatGPT followed the interview, albeit there were a few classics “I’m afraid I can’t do that”.
Full interview below.
Me: I'm your interviewer. We'll discuss crypto. Thanks for being interviewed. What do you think about cryptocurrency?
CGPT: Cryptocurrency is an innovative technology that could transform money and financial activities. It might boost the efficiency and security of financial institutions and let consumers deal directly without banks. Cryptocurrency is still a new and untested technology with many unknowns and hurdles before it can be broadly accepted.
Me: Over 22,000 cryptocurrencies exist, and many have little use. We need how much cryptocurrencies?
CGPT: The appropriate quantity will rely on a multitude of factors, including each cryptocurrency's use cases, adoption rate, and market rivalry. Only a few cryptocurrencies will likely receive widespread adoption and be successful. Many existing cryptocurrencies may not survive since they can't deliver new or valued solutions or compete with more established cryptocurrencies.
Me: Will cryptocurrencies grow? What's next for worldwide adoption?
CGPT: It's hard to forecast the future of cryptocurrencies because the acceptance of new technologies is unpredictable. I believe cryptocurrencies will expand and acquire popularity in the future years. Regulatory ambiguity, security concerns, and scalability issues must be overcome for this to happen. Cryptocurrency companies and organizations must engage together with governments and authorities to address these obstacles and establish a growth-friendly climate. Continued innovation and improvement of the technology, including public education and awareness, will drive acceptance.
Me: Do bear markets affect bitcoin adoption?
CGPT: On the one hand, a bear market might induce uncertainty and hesitation among potential consumers. Bear markets can present opportunities for long-term investors who can acquire cryptocurrencies at cheaper prices and are more likely to hang onto their assets. A bear market can also test the tenacity and power of the underlying technology and community, which can boost long-term confidence and adoption. A bear market might have profound and nuanced effects on bitcoin adoption.
Me: What are some likely outcomes if Bitcoin reaches $100,000 by next year?
CGPT: If Bitcoin saw rapid growth, it would undoubtedly have repercussions for the cryptocurrency market and economy. Possible scenarios include increased public interest and awareness of cryptocurrency, a surge in demand for Bitcoin and other cryptocurrencies, and a growth in the cryptocurrency industry's market value. By shifting their focus and cash to the cryptocurrency market, investors and traders may also affect other asset classes, such as traditional equities and commodities. Governments and financial organizations may focus more on the cryptocurrency sector as they try to grasp Bitcoin's rapid rise.
Me: Will other countries accept crypto as currency?
CGPT: It's hard to say if additional governments will adopt cryptocurrencies as legal tender. Some countries have recognized the promise of bitcoin and are exploring its use, while others are cautious. Adoption of bitcoin as legal cash may vary by country, based on financial infrastructure, rules, and political atmosphere. As cryptocurrency technology evolves and becomes more accepted, more governments may embrace it as legal tender.
Me: Final question: will the recent cryptocurrency hacks affect long term adoption?
CGPT: Hacks might tarnish cryptocurrency's reputation and public faith in its security, the technology underpinning it is continually improving. Many cryptocurrency projects have developed strong security mechanisms to prevent hacks and other dangers, and these safeguards will undoubtedly improve over time. The decentralized nature of cryptocurrency makes it more resistant to attacks. Hacks and other security breaches are a concern, but they may not affect cryptocurrency adoption.

Stephen Moore
3 years ago
Web 2 + Web 3 = Web 5.
Monkey jpegs and shitcoins have tarnished Web3's reputation. Let’s move on.

Web3 was called "the internet's future."
Well, 'crypto bros' shouted about it loudly.
As quickly as it arrived to be the next internet, it appears to be dead. It's had scandals, turbulence, and crashes galore:
Web 3.0's cryptocurrencies have crashed. Bitcoin's all-time high was $66,935. This month, Ethereum fell from $2130 to $1117. Six months ago, the cryptocurrency market peaked at $3 trillion. Worst is likely ahead.
Gas fees make even the simplest Web3 blockchain transactions unsustainable.
Terra, Luna, and other dollar pegs collapsed, hurting crypto markets. Celsius, a crypto lender backed by VCs and Canada's second-largest pension fund, and Binance, a crypto marketplace, have withheld money and coins. They're near collapse.
NFT sales are falling rapidly and losing public interest.
Web3 has few real-world uses, like most crypto/blockchain technologies. Web3's image has been tarnished by monkey profile pictures and shitcoins while failing to become decentralized (the whole concept is controlled by VCs).
The damage seems irreparable, leaving Web3 in the gutter.
Step forward our new saviour — Web5
Fear not though, as hero awaits to drag us out of the Web3 hellscape. Jack Dorsey revealed his plan to save the internet quickly.
Dorsey has long criticized Web3, believing that VC capital and silicon valley insiders have created a centralized platform. In a tweet that upset believers and VCs (he was promptly blocked by Marc Andreessen), Dorsey argued, "You don't own "Web3." VCs and LPs do. Their incentives prevent it. It's a centralized organization with a new name.
Dorsey announced Web5 on June 10 in a very Elon-like manner. Block's TBD unit will work on the project (formerly Square).
Web5's pitch is that users will control their own data and identity. Bitcoin-based. Sound familiar? The presentation pack's official definition emphasizes decentralization. Web5 is a decentralized web platform that enables developers to write decentralized web apps using decentralized identifiers, verifiable credentials, and decentralized web nodes, returning ownership and control over identity and data to individuals.
Web5 would be permission-less, open, and token-less. What that means for Earth is anyone's guess. Identity. Ownership. Blockchains. Bitcoin. Different.
Web4 appears to have been skipped, forever destined to wish it could have shown the world what it could have been. (It was probably crap.) As this iteration combines Web2 and Web3, simple math and common sense add up to 5. Or something.
Dorsey and his team have had this idea simmering for a while. Daniel Buchner, a member of Block's Decentralized Identity team, said, "We're finishing up Web5's technical components."
Web5 could be the project that decentralizes the internet. It must be useful to users and convince everyone to drop the countless Web3 projects, products, services, coins, blockchains, and websites being developed as I write this.
Web5 may be too late for Dorsey and the incoming flood of creators.
Web6 is planned!
The next months and years will be hectic and less stable than the transition from Web 1.0 to Web 2.0.
Web1 was around 1991-2004.
Web2 ran from 2004 to 2021. (though the Web3 term was first used in 2014, it only really gained traction years later.)
Web3 lasted a year.
Web4 is dead.
Silicon Valley billionaires are turning it into a startup-style race, each disrupting the next iteration until they crack it. Or destroy it completely.
Web5 won't last either.
David Z. Morris
3 years ago
FTX's crash was no accident, it was a crime

Sam Bankman Fried (SDBF) is a legendary con man. But the NYT might not tell you that...
Since SBF's empire was revealed to be a lie, mainstream news organizations and commentators have failed to give readers a straightforward assessment. The New York Times and Wall Street Journal have uncovered many key facts about the scandal, but they have also soft-peddled Bankman-Fried's intent and culpability.
It's clear that the FTX crypto exchange and Alameda Research committed fraud to steal money from users and investors. That’s why a recent New York Times interview was widely derided for seeming to frame FTX’s collapse as the result of mismanagement rather than malfeasance. A Wall Street Journal article lamented FTX's loss of charitable donations, bolstering Bankman's philanthropic pose. Matthew Yglesias, court chronicler of the neoliberal status quo, seemed to whitewash his own entanglements by crediting SBF's money with helping Democrats in 2020 – sidestepping the likelihood that the money was embezzled.
Many outlets have called what happened to FTX a "bank run" or a "run on deposits," but Bankman-Fried insists the company was overleveraged and disorganized. Both attempts to frame the fallout obscure the core issue: customer funds misused.
Because banks lend customer funds to generate returns, they can experience "bank runs." If everyone withdraws at once, they can experience a short-term cash crunch but there won't be a long-term problem.
Crypto exchanges like FTX aren't banks. They don't do bank-style lending, so a withdrawal surge shouldn't strain liquidity. FTX promised customers it wouldn't lend or use their crypto.
Alameda's balance sheet blurs SBF's crypto empire.
The funds were sent to Alameda Research, where they were apparently gambled away. This is massive theft. According to a bankruptcy document, up to 1 million customers could be affected.
In less than a month, reporting and the bankruptcy process have uncovered a laundry list of decisions and practices that would constitute financial fraud if FTX had been a U.S.-regulated entity, even without crypto-specific rules. These ploys may be litigated in U.S. courts if they enabled the theft of American property.
The list is very, very long.
The many crimes of Sam Bankman-Fried and FTX
At the heart of SBF's fraud are the deep and (literally) intimate ties between FTX and Alameda Research, a hedge fund he co-founded. An exchange makes money from transaction fees on user assets, but Alameda trades and invests its own funds.
Bankman-Fried called FTX and Alameda "wholly separate" and resigned as Alameda's CEO in 2019. The two operations were closely linked. Bankman-Fried and Alameda CEO Caroline Ellison were romantically linked.
These circumstances enabled SBF's sin. Within days of FTX's first signs of weakness, it was clear the exchange was funneling customer assets to Alameda for trading, lending, and investing. Reuters reported on Nov. 12 that FTX sent $10 billion to Alameda. As much as $2 billion was believed to have disappeared after being sent to Alameda. Now the losses look worse.
It's unclear why those funds were sent to Alameda or when Bankman-Fried betrayed his depositors. On-chain analysis shows most FTX to Alameda transfers occurred in late 2021, and bankruptcy filings show both lost $3.7 billion in 2021.
SBF's companies lost millions before the 2022 crypto bear market. They may have stolen funds before Terra and Three Arrows Capital, which killed many leveraged crypto players.
FTT loans and prints
CoinDesk's report on Alameda's FTT holdings ignited FTX and Alameda Research. FTX created this instrument, but only a small portion was traded publicly; FTX and Alameda held the rest. These holdings were illiquid, meaning they couldn't be sold at market price. Bankman-Fried valued its stock at the fictitious price.
FTT tokens were reportedly used as collateral for loans, including FTX loans to Alameda. Close ties between FTX and Alameda made the FTT token harder or more expensive to use as collateral, reducing the risk to customer funds.
This use of an internal asset as collateral for loans between clandestinely related entities is similar to Enron's 1990s accounting fraud. These executives served 12 years in prison.
Alameda's margin liquidation exemption
Alameda Research had a "secret exemption" from FTX's liquidation and margin trading rules, according to legal filings by FTX's new CEO.
FTX, like other crypto platforms and some equity or commodity services, offered "margin" or loans for trades. These loans are usually collateralized, meaning borrowers put up other funds or assets. If a margin trade loses enough money, the exchange will sell the user's collateral to pay off the initial loan.
Keeping asset markets solvent requires liquidating bad margin positions. Exempting Alameda would give it huge advantages while exposing other FTX users to hidden risks. Alameda could have kept losing positions open while closing out competitors. Alameda could lose more on FTX than it could pay back, leaving a hole in customer funds.
The exemption is criminal in multiple ways. FTX was fraudulently marketed overall. Instead of a level playing field, there were many customers.
Above them all, with shotgun poised, was Alameda Research.
Alameda front-running FTX listings
Argus says there's circumstantial evidence that Alameda Research had insider knowledge of FTX's token listing plans. Alameda was able to buy large amounts of tokens before the listing and sell them after the price bump.
If true, these claims would be the most brazenly illegal of Alameda and FTX's alleged shenanigans. Even if the tokens aren't formally classified as securities, insider trading laws may apply.
In a similar case this year, an OpenSea employee was charged with wire fraud for allegedly insider trading. This employee faces 20 years in prison for front-running monkey JPEGs.
Huge loans to executives
Alameda Research reportedly lent FTX executives $4.1 billion, including massive personal loans. Bankman-Fried received $1 billion in personal loans and $2.3 billion for an entity he controlled, Paper Bird. Nishad Singh, director of engineering, was given $543 million, and FTX Digital Markets co-CEO Ryan Salame received $55 million.
FTX has more smoking guns than a Texas shooting range, but this one is the smoking bazooka – a sign of criminal intent. It's unclear how most of the personal loans were used, but liquidators will have to recoup the money.
The loans to Paper Bird were even more worrisome because they created another related third party to shuffle assets. Forbes speculates that some Paper Bird funds went to buy Binance's FTX stake, and Paper Bird committed hundreds of millions to outside investments.
FTX Inner Circle: Who's Who
That included many FTX-backed VC funds. Time will tell if this financial incest was criminal fraud. It fits Bankman-pattern Fried's of using secret flows, leverage, and funny money to inflate asset prices.
FTT or loan 'bailouts'
Also. As the crypto bear market continued in 2022, Bankman-Fried proposed bailouts for bankrupt crypto lenders BlockFi and Voyager Digital. CoinDesk was among those deceived, welcoming SBF as a J.P. Morgan-style sector backstop.
In a now-infamous interview with CNBC's "Squawk Box," Bankman-Fried referred to these decisions as bets that may or may not pay off.
But maybe not. Bloomberg's Matt Levine speculated that FTX backed BlockFi with FTT money. This Monopoly bailout may have been intended to hide FTX and Alameda liabilities that would have been exposed if BlockFi went bankrupt sooner. This ploy has no name, but it echoes other corporate frauds.
Secret bank purchase
Alameda Research invested $11.5 million in the tiny Farmington State Bank, doubling its net worth. As a non-U.S. entity and an investment firm, Alameda should have cleared regulatory hurdles before acquiring a U.S. bank.
In the context of FTX, the bank's stake becomes "ominous." Alameda and FTX could have done more shenanigans with bank control. Compare this to the Bank for Credit and Commerce International's failed attempts to buy U.S. banks. BCCI was even nefarious than FTX and wanted to buy U.S. banks to expand its money-laundering empire.
The mainstream's mistakes
These are complex and nuanced forms of fraud that echo traditional finance models. This obscurity helped Bankman-Fried masquerade as an honest player and likely kept coverage soft after the collapse.
Bankman-Fried had a scruffy, nerdy image, like Mark Zuckerberg and Adam Neumann. In interviews, he spoke nonsense about an industry full of jargon and complicated tech. Strategic donations and insincere ideological statements helped him gain political and social influence.
SBF' s'Effective' Altruism Blew Up FTX
Bankman-Fried has continued to muddy the waters with disingenuous letters, statements, interviews, and tweets since his con collapsed. He's tried to portray himself as a well-intentioned but naive kid who made some mistakes. This is a softer, more pernicious version of what Trump learned from mob lawyer Roy Cohn. Bankman-Fried doesn't "deny, deny, deny" but "confuse, evade, distort."
It's mostly worked. Kevin O'Leary, who plays an investor on "Shark Tank," repeats Bankman-SBF's counterfactuals. O'Leary called Bankman-Fried a "savant" and "probably one of the most accomplished crypto traders in the world" in a Nov. 27 interview with Business Insider, despite recent data indicating immense trading losses even when times were good.
O'Leary's status as an FTX investor and former paid spokesperson explains his continued affection for Bankman-Fried despite contradictory evidence. He's not the only one promoting Bankman-Fried. The disgraced son of two Stanford law professors will defend himself at Wednesday's DealBook Summit.
SBF's fraud and theft rival those of Bernie Madoff and Jho Low. Whether intentionally or through malign ineptitude, the fraud echoes Worldcom and Enron.
The Perverse Impacts of Anti-Money-Laundering
The principals in all of those scandals wound up either sentenced to prison or on the run from the law. Sam Bankman-Fried clearly deserves to share their fate.
Read the full article here.
You might also like
Vanessa Karel
3 years ago
10 hard lessons from founding a startup.
Here is the ugly stuff, read this if you have a founder in your life or are trying to become one. Your call.

#1 You'll try to talk yourself to sleep, but it won't always work.
As founders, we're all driven. Good and bad, you're restless. Success requires resistance and discipline. Your startup will be on your mind 24/7, and not everyone will have the patience to listen to your worries, ideas, and coffee runs. You become more self-sufficient than ever before.
#2 No one will understand what you're going through unless they've been a founder.
Some of my closest friends don't understand the work that goes into starting a business, and we can't blame them.
#3 You'll feel alienated.
Your problems aren't common; calling your bestie won't help. You must search hard for the right resources. It alienates you from conversations you no longer relate to. (No 4th of July, no long weekends!)
#4 Since you're your "own boss," people assume you have lots of free time.
Do you agree? I was on a webinar with lots of new entrepreneurs, and one woman said, "I started my own business so I could have more time for myself." This may be true for some lucky people, and you can be flexible with your schedule. If you want your business to succeed, you'll probably be its slave for a while.
#5 No time for illness or family emergencies.
Both last month. Oh, no! Physically and emotionally withdrawing at the worst times will give you perspective. I learned this the hard way because I was too stubborn to postpone an important interview. I thought if I rested all day and only took one call, I'd be fine. Nope. I had a fever and my mind wasn't as sharp, so my performance and audience interaction suffered. Nope. Better to delay than miss out.
Oh, and setting a "OoO" makes you cringe.
#6 Good luck with your mental health, perfectionists.
When building a startup, it's difficult to accept that there won't be enough time to do everything. You can't make them all, not perfectly. You must learn to accept things that are done but not perfect.
#7 As a founder, you'll make mistakes, but you'll want to make them quickly so you can learn.
Hard lessons are learned quicker. You'll need to pivot and try new things often; some won't work, and it's best to discover them sooner rather than later.
#8 Pyramid schemes abound.
I didn't realize how bad it was until I started a company. You must spy and constantly research. As a founder, you'll receive many emails from people claiming to "support" you. Be wary and keep your eyes open. When it's too good to be true. Some "companies" will try to get you to pay for "competitions" to "pitch at events." Don't do it.
#9 Keep your competitor research to a minimum.
Actually, competition is good. It means there's a market for those solutions. However, this can be mentally exhausting too. Learn about their geography and updates, but that's it.
#10 You'll feel guilty taking vacation.
I don't know what to say, but I no longer enjoy watching TV, and that's okay. Pay attention to things that enrich you, bring you joy, and have fun. It boosts creativity.
Being a startup founder may be one of the hardest professional challenges you face, but it's also a great learning experience. Your passion will take you places you never imagined and open doors to opportunities you wouldn't have otherwise. You'll meet amazing people. No regrets, no complaints. It's a roller coaster, but the good days are great.
Miss anything? Comment below

David G Chen
3 years ago
If you want to earn money, stop writing for entertainment.
When you stop blogging for a few weeks, your views and profits plummet.
Because you're writing fascinating posts for others. Everyone's done ithat…
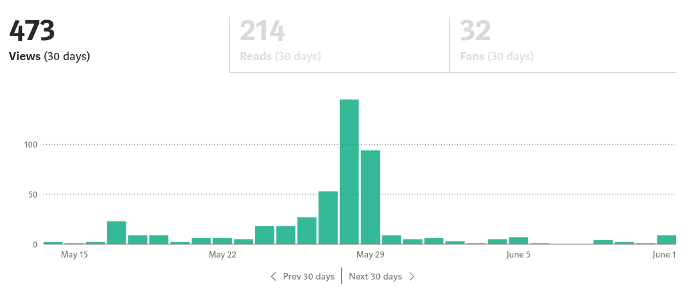
If I keep writing, the graph should maintain velocity, you could say. If I wrote more, it could rise.
However, entertaining pieces still tend to roller coaster and jump.
this type of writing is like a candle. They burn out and must be replaced. You must continuously light new ones to maintain the illumination.
When you quit writing, your income stops.
A substitute
Instead of producing amusing articles, try solving people's issues. You should answer their search questions.
Here's what happens when you answer their searches.
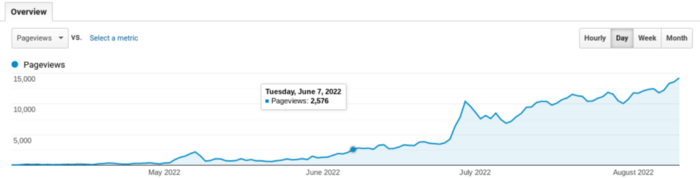
My website's Google analytics. As a dentist, I answer oral health questions.
This chart vs. Medium is pretty glaring, right?
As of yesterday, it was averaging 15k page views each day.
How much would you make on Medium with 15k daily views?
Evergreen materials
In SEO, this is called evergreen content.
Your content is like a lush, evergreen forest, and by green I mean Benjamins.

Do you have knowledge that you can leverage? Why not help your neighbors and the world?
Answer search inquiries and help others. You'll be well rewarded.
This is better than crafting candle-like content that fizzles out quickly.
Is beauty really ephemeral like how flowers bloom? Nah, I prefer watching forests grow instead (:
Matt Nutsch
3 years ago
Most people are unaware of how artificial intelligence (A.I.) is changing the world.

Recently, I saw an interesting social media post. In an entrepreneurship forum. A blogger asked for help because he/she couldn't find customers. I now suspect that the writer’s occupation is being disrupted by A.I.
Introduction
Artificial Intelligence (A.I.) has been a hot topic since the 1950s. With recent advances in machine learning, A.I. will touch almost every aspect of our lives. This article will discuss A.I. technology and its social and economic implications.
What's AI?
A computer program or machine with A.I. can think and learn. In general, it's a way to make a computer smart. Able to understand and execute complex tasks. Machine learning, NLP, and robotics are common types of A.I.
AI's global impact

AI will change the world, but probably faster than you think. A.I. already affects our daily lives. It improves our decision-making, efficiency, and productivity.
A.I. is transforming our lives and the global economy. It will create new business and job opportunities but eliminate others. Affected workers may face financial hardship.
AI examples:
OpenAI's GPT-3 text-generation

Developers can train, deploy, and manage models on GPT-3. It handles data preparation, model training, deployment, and inference for machine learning workloads. GPT-3 is easy to use for both experienced and new data scientists.
My team conducted an experiment. We needed to generate some blog posts for a website. We hired a blogger on Upwork. OpenAI created a blog post. The A.I.-generated blog post was of higher quality and lower cost.
MidjourneyAI's Art Contests

AI already affects artists. Artists use A.I. to create realistic 3D images and videos for digital art. A.I. is also used to generate new art ideas and methods.
MidjourneyAI and GigapixelAI won a contest last month. It's AI. created a beautiful piece of art that captured the contest's spirit. AI triumphs. It could open future doors.
After the art contest win, I registered to try out these new image generating A.I.s. In the MidjourneyAI chat forum, I noticed an artist's plea. The artist begged others to stop flooding RedBubble with AI-generated art.
Shutterstock and Getty Images have halted user uploads. AI-generated images flooded online marketplaces.
Imagining Videos with Meta

Meta released Make-a-Video this week. It's an A.I. app that creates videos from text. What you type creates a video.
This technology will impact TV, movies, and video games greatly. Imagine a movie or game that's personalized to your tastes. It's closer than you think.
Uses and Abuses of Deepfakes

Deepfake videos are computer-generated images of people. AI creates realistic images and videos of people.
Deepfakes are entertaining but have social implications. Porn introduced deepfakes in 2017. People put famous faces on porn actors and actresses without permission.
Soon, deepfakes were used to show dead actors/actresses or make them look younger. Carrie Fischer was included in films after her death using deepfake technology.
Deepfakes can be used to create fake news or manipulate public opinion, according to an AI.
Voices for Darth Vader and Iceman
James Earl Jones, who voiced Darth Vader, sold his voice rights this week. Aged actor won't be in those movies. Respeecher will use AI to mimic Jones's voice. This technology could change the entertainment industry. One actor can now voice many characters.

AI can generate realistic voice audio from text. Top Gun 2 actor Val Kilmer can't speak for medical reasons. Sonantic created Kilmer's voice from the movie script. This entertaining technology has social implications. It blurs authentic recordings and fake media.
Medical A.I. fights viruses
A team of Chinese scientists used machine learning to predict effective antiviral drugs last year. They started with a large dataset of virus-drug interactions. Researchers combined that with medication and virus information. Finally, they used machine learning to predict effective anti-virus medicines. This technology could solve medical problems.
AI ideas AI-generated Itself

OpenAI's GPT-3 predicted future A.I. uses. Here's what it told me:
AI will affect the economy. Businesses can operate more efficiently and reinvest resources with A.I.-enabled automation. AI can automate customer service tasks, reducing costs and improving satisfaction.
A.I. makes better pricing, inventory, and marketing decisions. AI automates tasks and makes decisions. A.I.-powered robots could help the elderly or disabled. Self-driving cars could reduce accidents.
A.I. predictive analytics can predict stock market or consumer behavior trends and patterns. A.I. also personalizes recommendations. sways. A.I. recommends products and movies. AI can generate new ideas based on data analysis.
Conclusion

A.I. will change business as it becomes more common. It will change how we live and work by creating growth and prosperity.
Exciting times, but also one which should give us all pause. Technology can be good or evil. We must use new technologies ethically, fairly, and honestly.
“The author generated some sentences in this text in part with GPT-3, OpenAI’s large-scale language-generation model. Upon generating draft language, the author reviewed, edited, and revised the language to their own liking and takes ultimate responsibility for the content of this publication. The text of this post was further edited using HemingWayApp. Many of the images used were generated using A.I. as described in the captions.”
