More on Web3 & Crypto
James Howell
3 years ago
Which Metaverse Is Better, Decentraland or Sandbox?
The metaverse is the most commonly used term in current technology discussions. While the entire tech ecosystem awaits the metaverse's full arrival, defining it is difficult. Imagine the internet in the '80s! The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
The metaverse is a three-dimensional virtual world where users can interact with digital solutions and each other as digital avatars.
Among the metaverse hype, the Decentraland vs Sandbox debate has gained traction. Both are decentralized metaverse platforms with no central authority. So, what's the difference and which is better? Let us examine the distinctions between Decentraland and Sandbox.
2 Popular Metaverse Platforms Explained
The first step in comparing sandbox and Decentraland is to outline the definitions. Anyone keeping up with the metaverse news has heard of the two current leaders. Both have many similarities, but also many differences. Let us start with defining both platforms to see if there is a winner.
Decentraland
Decentraland, a fully immersive and engaging 3D metaverse, launched in 2017. It allows players to buy land while exploring the vast virtual universe. Decentraland offers a wide range of activities for its visitors, including games, casinos, galleries, and concerts. It is currently the longest-running metaverse project.
Decentraland began with a $24 million ICO and went public in 2020. The platform's virtual real estate parcels allow users to create a variety of experiences. MANA and LAND are two distinct tokens associated with Decentraland. MANA is the platform's native ERC-20 token, and users can burn MANA to get LAND, which is ERC-721 compliant. The MANA coin can be used to buy avatars, wearables, products, and names on Decentraland.
Sandbox
Sandbox, the next major player, began as a blockchain-based virtual world in 2011 and migrated to a 3D gaming platform in 2017. The virtual world allows users to create, play, own, and monetize their virtual experiences. Sandbox aims to empower artists, creators, and players in the blockchain community to customize the platform. Sandbox gives the ideal means for unleashing creativity in the development of the modern gaming ecosystem.
The project combines NFTs and DAOs to empower a growing community of gamers. A new play-to-earn model helps users grow as gamers and creators. The platform offers a utility token, SAND, which is required for all transactions.
What are the key points from both metaverse definitions to compare Decentraland vs sandbox?
It is ideal for individuals, businesses, and creators seeking new artistic, entertainment, and business opportunities. It is one of the rapidly growing Decentralized Autonomous Organization projects. Holders of MANA tokens also control the Decentraland domain.
Sandbox, on the other hand, is a blockchain-based virtual world that runs on the native token SAND. On the platform, users can create, sell, and buy digital assets and experiences, enabling blockchain-based gaming. Sandbox focuses on user-generated content and building an ecosystem of developers.
Sandbox vs. Decentraland
If you try to find what is better Sandbox or Decentraland, then you might struggle with only the basic definitions. Both are metaverse platforms offering immersive 3D experiences. Users can freely create, buy, sell, and trade digital assets. However, both have significant differences, especially in MANA vs SAND.
For starters, MANA has a market cap of $5,736,097,349 versus $4,528,715,461, giving Decentraland an advantage.
The MANA vs SAND pricing comparison is also noteworthy. A SAND is currently worth $3664, while a MANA is worth $2452.
The value of the native tokens and the market capitalization of the two metaverse platforms are not enough to make a choice. Let us compare Sandbox vs Decentraland based on the following factors.
Workstyle
The way Decentraland and Sandbox work is one of the main comparisons. From a distance, they both appear to work the same way. But there's a lot more to learn about both platforms' workings. Decentraland has 90,601 digital parcels of land.
Individual parcels of virtual real estate or estates with multiple parcels of land are assembled. It also has districts with similar themes and plazas, which are non-tradeable parcels owned by the community. It has three token types: MANA, LAND, and WEAR.
Sandbox has 166,464 plots of virtual land that can be grouped into estates. Estates are owned by one person, while districts are owned by two or more people. The Sandbox metaverse has four token types: SAND, GAMES, LAND, and ASSETS.
Age
The maturity of metaverse projects is also a factor in the debate. Decentraland is clearly the winner in terms of maturity. It was the first solution to create a 3D blockchain metaverse. Decentraland made the first working proof of concept public. However, Sandbox has only made an Alpha version available to the public.
Backing
The MANA vs SAND comparison would also include support for both platforms. Digital Currency Group, FBG Capital, and CoinFund are all supporters of Decentraland. It has also partnered with Polygon, the South Korean government, Cyberpunk, and Samsung.
SoftBank, a Japanese multinational conglomerate focused on investment management, is another major backer. Sandbox has the backing of one of the world's largest investment firms, as well as Slack and Uber.
Compatibility
Wallet compatibility is an important factor in comparing the two metaverse platforms. Decentraland currently has a competitive advantage. How? Both projects' marketplaces accept ERC-20 wallets. However, Decentraland has recently improved by bridging with Walletconnect. So it can let Polygon users join Decentraland.
Scalability
Because Sandbox and Decentraland use the Ethereum blockchain, scalability is an issue. Both platforms' scalability is constrained by volatile tokens and high gas fees. So, scalability issues can hinder large-scale adoption of both metaverse platforms.
Buying Land
Decentraland vs Sandbox comparisons often include virtual real estate. However, the ability to buy virtual land on both platforms defines the user experience and differentiates them. In this case, Sandbox offers better options for users to buy virtual land by combining OpenSea and Sandbox. In fact, Decentraland users can only buy from the MANA marketplace.
Innovation
The rate of development distinguishes Sandbox and Decentraland. Both platforms have been developing rapidly new features. However, Sandbox wins by adopting Polygon NFT layer 2 solutions, which consume almost 100 times less energy than Ethereum.
Collaborations
The platforms' collaborations are the key to determining "which is better Sandbox or Decentraland." Adoption of metaverse platforms like the two in question can be boosted by association with reputable brands. Among the partners are Atari, Cyberpunk, and Polygon. Rather, Sandbox has partnered with well-known brands like OpenSea, CryptoKitties, The Walking Dead, Snoop Dogg, and others.
Platform Adaptivity
Another key feature that distinguishes Sandbox and Decentraland is the ease of use. Sandbox clearly wins in terms of platform access. It allows easy access via social media, email, or a Metamask wallet. However, Decentraland requires a wallet connection.
Prospects
The future development plans also play a big role in defining Sandbox vs Decentraland. Sandbox's future development plans include bringing the platform to mobile devices. This includes consoles like PlayStation and Xbox. By the end of 2023, the platform expects to have around 5000 games.
Decentraland, on the other hand, has no set plan. In fact, the team defines the decisions that appear to have value. They plan to add celebrities, creators, and brands soon, along with NFT ads and drops.
Final Words
The comparison of Decentraland vs Sandbox provides a balanced view of both platforms. You can see how difficult it is to determine which decentralized metaverse is better now. Sandbox is still in Alpha, whereas Decentraland has a working proof of concept.
Sandbox, on the other hand, has better graphics and is backed by some big names. But both have a long way to go in the larger decentralized metaverse.

CyberPunkMetalHead
3 years ago
195 countries want Terra Luna founder Do Kwon
Interpol has issued a red alert on Terraform Labs' CEO, South Korean prosecutors said.

After the May crash of Terra Luna revealed tax evasion issues, South Korean officials filed an arrest warrant for Do Kwon, but he is missing.
Do Kwon is now a fugitive in 195 countries after Seoul prosecutors placed him to Interpol's red list. Do Kwon hasn't commented since then. The red list allows any country's local authorities to apprehend Do Kwon.
Do Dwon and Terraform Labs were believed to have moved to Singapore days before the $40 billion wipeout, but Singapore authorities said he fled the country on September 17. Do Kwon tweeted that he wasn't on the run and cited privacy concerns.
Do Kwon was not on the red list at the time and said he wasn't "running," only to reply to his own tweet saying he hasn't jogged in a while and needed to trim calories.
Whether or not it makes sense to read too much into this, the reality is that Do Kwon is now on Interpol red list, despite the firmly asserts on twitter that he does absolutely nothing to hide.
UPDATE:
South Korean authorities are investigating alleged withdrawals of over $60 million U.S. and seeking to freeze these assets. Korean authorities believe a new wallet exchanged over 3000 BTC through OKX and Kucoin.
Do Kwon and the Luna Foundation Guard (of whom Do Kwon is a key member of) have declined all charges and dubbed this disinformation.
Singapore's Luna Foundation Guard (LFG) manages the Terra Ecosystem.
The Legal Situation
Multiple governments are searching for Do Kwon and five other Terraform Labs employees for financial markets legislation crimes.
South Korean authorities arrested a man suspected of tax fraud and Ponzi scheme.
The U.S. SEC is also examining Terraform Labs on how UST was advertised as a stablecoin. No legal precedent exists, so it's unclear what's illegal.
The future of Terraform Labs, Terra, and Terra 2 is unknown, and despite what Twitter shills say about LUNC, the company remains in limbo awaiting a decision that will determine its fate. This project isn't a wise investment.

Ryan Weeks
3 years ago
Terra fiasco raises TRON's stablecoin backstop
After Terra's algorithmic stablecoin collapsed in May, TRON announced a plan to increase the capital backing its own stablecoin.
USDD, a near-carbon copy of Terra's UST, arrived on the TRON blockchain on May 5. TRON founder Justin Sun says USDD will be overcollateralized after initially being pegged algorithmically to the US dollar.
A reserve of cryptocurrencies and stablecoins will be kept at 130 percent of total USDD issuance, he said. TRON described the collateral ratio as "guaranteed" and said it would begin publishing real-time updates on June 5.
Currently, the reserve contains 14,040 bitcoin (around $418 million), 140 million USDT, 1.9 billion TRX, and 8.29 billion TRX in a burning contract.
Sun: "We want to hybridize USDD." We have an algorithmic stablecoin and TRON DAO Reserve.
algorithmic failure
USDD was designed to incentivize arbitrageurs to keep its price pegged to the US dollar by trading TRX, TRON's token, and USDD. Like Terra, TRON signaled its intent to establish a bitcoin and cryptocurrency reserve to support USDD in extreme market conditions.
Still, Terra's UST failed despite these safeguards. The stablecoin veered sharply away from its dollar peg in mid-May, bringing down Terra's LUNA and wiping out $40 billion in value in days. In a frantic attempt to restore the peg, billions of dollars in bitcoin were sold and unprecedented volumes of LUNA were issued.
Sun believes USDD, which has a total circulating supply of $667 million, can be backed up.
"Our reserve backing is diversified." Bitcoin and stablecoins are included. USDC will be a small part of Circle's reserve, he said.
TRON's news release lists the reserve's assets as bitcoin, TRX, USDC, USDT, TUSD, and USDJ.
All Bitcoin addresses will be signed so everyone knows they belong to us, Sun said.
Not giving in
Sun told that the crypto industry needs "decentralized" stablecoins that regulators can't touch.
Sun said the Luna Foundation Guard, a Singapore-based non-profit that raised billions in cryptocurrency to buttress UST, mismanaged the situation by trying to sell to panicked investors.
He said, "We must be ahead of the market." We want to stabilize the market and reduce volatility.
Currently, TRON finances most of its reserve directly, but Sun says the company hopes to add external capital soon.
Before its demise, UST holders could park the stablecoin in Terra's lending platform Anchor Protocol to earn 20% interest, which many deemed unsustainable. TRON's JustLend is similar. Sun hopes to raise annual interest rates from 17.67% to "around 30%."
This post is a summary. Read full article here
You might also like

Will Lockett
2 years ago
There Is A New EV King in Town

McMurtry Spéirling outperforms Tesla in speed and efficiency.
EVs were ridiculously slow for decades. However, the 2008 Tesla Roadster revealed that EVs might go extraordinarily fast. The Tesla Model S Plaid and Rimac Nevera are the fastest-accelerating road vehicles, despite combustion-engined road cars dominating the course. A little-known firm beat Tesla and Rimac in the 0-60 race, beat F1 vehicles on a circuit, and boasts a 350-mile driving range. The McMurtry Spéirling is completely insane.
Mat Watson of CarWow, a YouTube megastar, was recently handed a Spéirling and access to Silverstone Circuit (view video above). Mat ran a quarter-mile on Silverstone straight with former F1 driver Max Chilton. The little pocket-rocket automobile touched 100 mph in 2.7 seconds, completed the quarter mile in 7.97 seconds, and hit 0-60 in 1.4 seconds. When looking at autos quickly, 0-60 times can seem near. The Tesla Model S Plaid does 0-60 in 1.99 seconds, which is comparable to the Spéirling. Despite the meager statistics, the Spéirling is nearly 30% faster than Plaid!
My vintage VW Golf 1.4s has an 8.8-second 0-60 time, whereas a BMW Z4 3.0i is 30% faster (with a 0-60 time of 6 seconds). I tried to beat a Z4 off the lights in my Golf, but the Beamer flew away. If they challenge the Spéirling in a Model S Plaid, they'll feel as I did. Fast!
Insane quarter-mile drag time. Its road car record is 7.97 seconds. A Dodge Demon, meant to run extremely fast quarter miles, finishes so in 9.65 seconds, approximately 20% slower. The Rimac Nevera's 8.582-second quarter-mile record was miles behind drag racing. This run hampered the Spéirling. Because it was employing gearing that limited its top speed to 150 mph, it reached there in a little over 5 seconds without accelerating for most of the quarter mile! McMurtry can easily change the gearing, making the Spéirling run quicker.
McMurtry did this how? First, the Spéirling is a tiny single-seater EV with a 60 kWh battery pack, making it one of the lightest EVs ever. The 1,000-hp Spéirling has more than one horsepower per kg. The Nevera has 0.84 horsepower per kg and the Plaid 0.44.
However, you cannot simply construct a car light and power it. Instead of accelerating, it would spin. This makes the Spéirling a fan car. Its huge fans create massive downforce. These fans provide the Spéirling 2 tonnes of downforce while stationary, so you could park it on the ceiling. Its fast 0-60 time comes from its downforce, which lets it deliver all that power without wheel spin.
It also possesses complete downforce at all speeds, allowing it to tackle turns faster than even race vehicles. Spéirlings overcame VW IDRs and F1 cars to set the Goodwood Hill Climb record (read more here). The Spéirling is a dragstrip winner and track dominator, unlike the Plaid and Nevera.
The Spéirling is astonishing for a single-seater. Fan-generated downforce is more efficient than wings and splitters. It also means the vehicle has very minimal drag without the fan. The Spéirling can go 350 miles per charge (WLTP) or 20-30 minutes at full speed on a track despite its 60 kWh battery pack. The G-forces would hurt your neck before the battery died if you drove around a track for longer. The Spéirling can charge at over 200 kW in about 30 minutes. Thus, driving to track days, having fun, and returning is possible. Unlike other high-performance EVs.
Tesla, Rimac, or Lucid will struggle to defeat the Spéirling. They would need to build a fan automobile because adding power to their current vehicle would make it uncontrollable. The EV and automobile industries now have a new, untouchable performance king.

Jack Shepherd
3 years ago
A Dog's Guide to Every Type of Zoom Call Participant
Are you one of these Zoom dogs?
The Person Who Is Apparently Always on Mute
Waffles thinks he can overpower the mute button by shouting loudly.
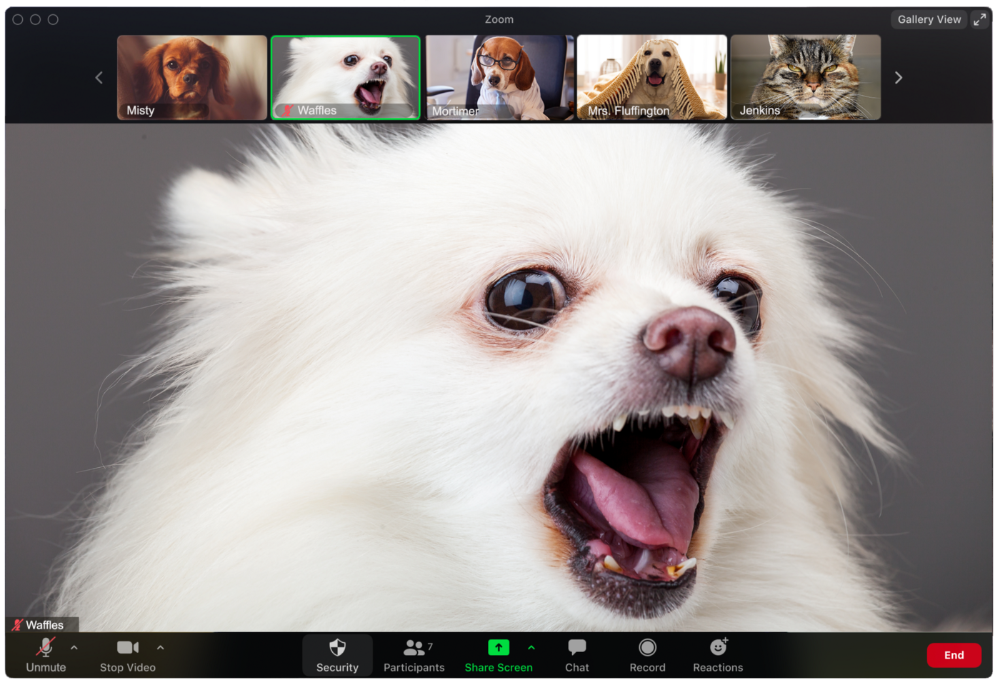
The person who believed their camera to be off
Barkley's used to remote work, but he hasn't mastered the "Stop Video" button. Everyone is affected.
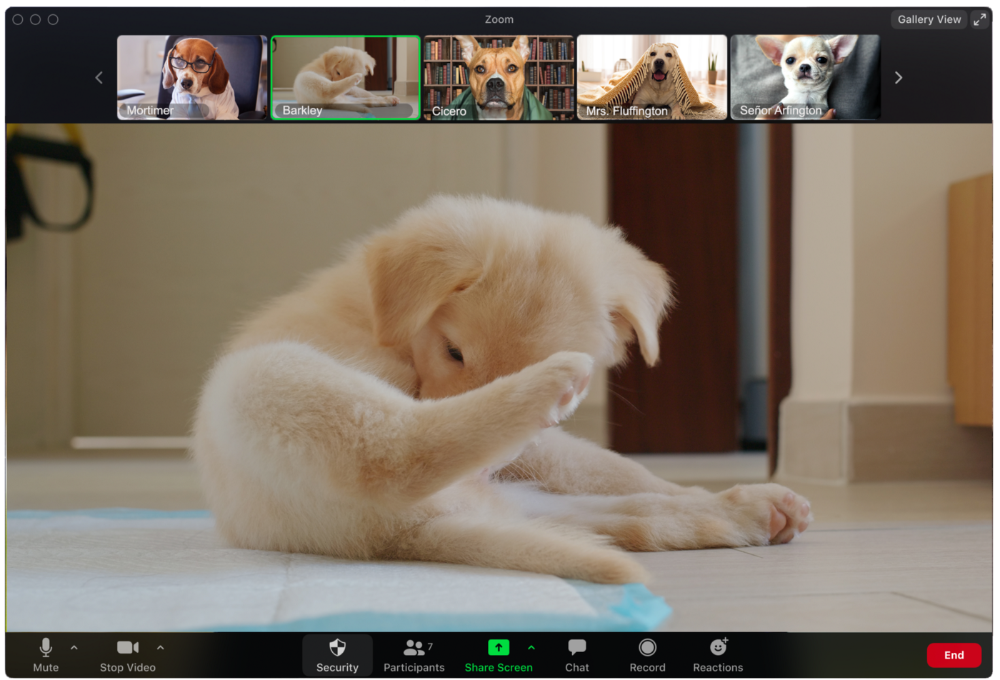
Who is driving for some reason, exactly?
Why is Pumpkin always late? Who knows? Shouldn't she be driving? If you could hear her over the freeway, she'd answer these questions.
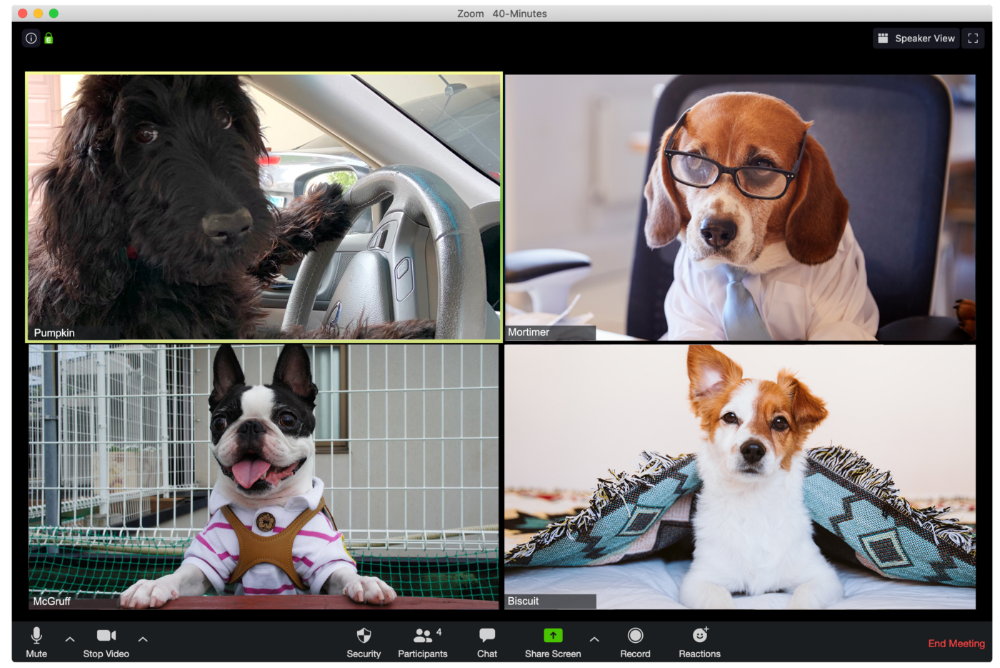
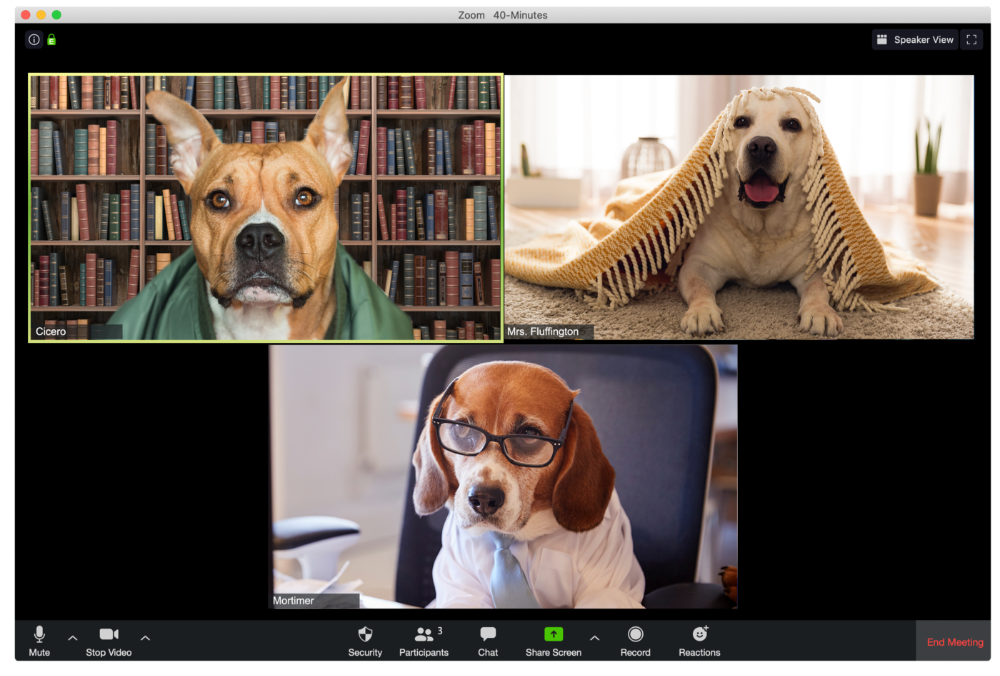
The Person With the Amazing Bookcase
Cicero likes to use SAT-words like "leverage" and "robust" in Zoom sessions, presumably from all the books he wants you to see behind him.
The Individual Who Is Unnecessarily Dressed
We hope Bandit is going somewhere beautiful after this meeting, or else he neglected the quarterly earnings report and is overcompensating to distract us.
The person who works through lunch in between zoom calls
Barksworth has back-to-back meetings all day, so you can watch her eat while she talks.
The Person Who Is A Little Too Comfy
Hercules thinks Zoom meetings happen between sleeps. He'd appreciate everyone speaking more quietly.
The Person Who Answered the Phone Outside
Frisbee has a gorgeous backyard and lives in a place with great weather year-round, and she wants you to think about that during the daily team huddle.
Who Wants You to Pay Attention to Their Pet
Snickers hasn't listened to you in 20 minutes unless you tell her how cute her kitten is.
One who is, for some reason, positioned incorrectly on the screen
Nelson's meetings consist primarily of attempting to figure out how he positioned his laptop so absurdly.

The person who says too many goodbyes
Zeus waves farewell like it's your first day of school while everyone else searches for the "Leave Meeting" button. It's nice.
He who has a poor internet connection
Ziggy's connectivity problems continue... She gives a long speech as everyone waits awkwardly to inform her they missed it.
The Clearly Multitasking Person
Tinkerbell can play fetch during the monthly staff meeting if she works from home, but that's not a good idea.
The Person Using Zoom as a Makeup and Hair Mirror
If Gail and Bob knew Zoom had a "hide self view" option, they'd be distraught.

The person who feels at ease with simply leaving
Rusty bails when a Zoom conference is over. Rusty's concept is decent.

Woo
3 years ago
How To Launch A Business Without Any Risk
> Say Hello To The Lean-Hedge Model
People think starting a business requires significant debt and investment. Like Shark Tank, you need a world-changing idea. I'm not saying to avoid investors or brilliant ideas.
Investing is essential to build a genuinely profitable company. Think Apple or Starbucks.
Entrepreneurship is risky because many people go bankrupt from debt. As starters, we shouldn't do it. Instead, use lean-hedge.
Simply defined, you construct a cash-flow business to hedge against long-term investment-heavy business expenses.
What the “fx!$rench-toast” is the lean-hedge model?
When you start a business, your money should move down, down, down, then up when it becomes profitable.
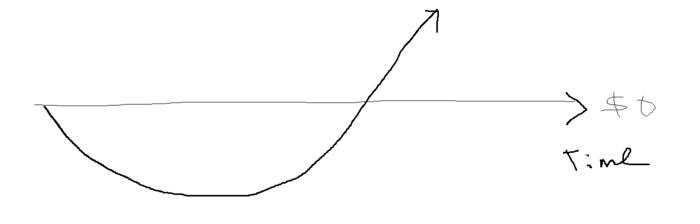
Many people don't survive the business's initial losses and debt. What if, we created a cash-flow business BEFORE we started our Starbucks to hedge against its initial expenses?
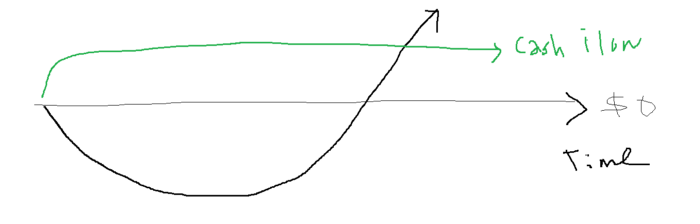
Lean-hedge has two sections. Start a cash-flow business. A cash-flow business takes minimal investment and usually involves sweat and time.
Let’s take a look at some examples:
A Translation company
Personal portfolio website (you make a site then you do cold e-mail marketing)
FREELANCE (UpWork, Fiverr).
Educational business.
Infomarketing. (You design a knowledge-based product. You sell the info).
Online fitness/diet/health coaching ($50-$300/month, calls, training plan)
Amazon e-book publishing. (Medium writers do this)
YouTube, cash-flow channel
A web development agency (I'm a dev, but if you're not, a graphic design agency, etc.) (Sell your time.)
Digital Marketing
Online paralegal (A million lawyers work in the U.S).
Some dropshipping (Organic Tik Tok dropshipping, where you create content to drive traffic to your shopify store instead of spend money on ads).
(Disclaimer: My first two cash-flow enterprises, which were language teaching, failed terribly. My translation firm is now booming because B2B e-mail marketing is easy.)
Crossover occurs. Your long-term business starts earning more money than your cash flow business.
My cash-flow business (freelancing, translation) makes $7k+/month.
I’ve decided to start a slightly more investment-heavy digital marketing agency
Here are the anticipated business's time- and money-intensive investments:
($$$) Top Front-End designer's Figma/UI-UX design (in negotiation)
(Time): A little copywriting (I will do this myself)
($$) Creating an animated webpage with HTML (in negotiation)
Backend Development (Duration) (I'll carry out this myself using Laravel.)
Logo Design ($$)
Logo Intro Video for $
Video Intro (I’ll edit this myself with Premiere Pro)
etc.
Then evaluate product, place, price, and promotion. Consider promotion and pricing.
The lean-hedge model's point is:
Don't gamble. Avoid debt. First create a cash-flow project, then grow it steadily.
Check read my previous posts on “Nightmare Mode” (which teaches you how to make work as interesting as video games) and Why most people can't escape a 9-5 to learn how to develop a cash-flow business.
