More on Web3 & Crypto

Miguel Saldana
3 years ago
Crypto Inheritance's Catch-22
Security, privacy, and a strategy!

How to manage digital assets in worst-case scenarios is a perennial crypto concern. Since blockchain and bitcoin technology is very new, this hasn't been a major issue. Many early developers are still around, and many groups created around this technology are young and feel they have a lot of life remaining. This is why inheritance and estate planning in crypto should be handled promptly. As cryptocurrency's intrinsic worth rises, many people in the ecosystem are holding on to assets that might represent generational riches. With that much value, it's crucial to have a plan. Creating a solid plan entails several challenges.
the initial hesitation in coming up with a plan
The technical obstacles to ensuring the assets' security and privacy
the passing of assets from a deceased or incompetent person
Legal experts' lack of comprehension and/or understanding of how to handle and treat cryptocurrency.
This article highlights several challenges, a possible web3-native solution, and how to learn more.

The Challenge of Inheritance:
One of the biggest hurdles to inheritance planning is starting the conversation. As humans, we don't like to think about dying. Early adopters will experience crazy gains as cryptocurrencies become more popular. Creating a plan is crucial if you wish to pass on your riches to loved ones. Without a plan, the technical and legal issues I barely mentioned above would erode value by requiring costly legal fees and/or taxes, and you could lose everything if wallets and assets are not distributed appropriately (associated with the private keys). Raising awareness of the consequences of not having a plan should motivate people to make one.

Controlling Change:
Having an inheritance plan for your digital assets is crucial, but managing the guts and bolts poses a new set of difficulties. Privacy and security provided by maintaining your own wallet provide different issues than traditional finances and assets. Traditional finance is centralized (say a stock brokerage firm). You can assign another person to handle the transfer of your assets. In crypto, asset transfer is reimagined. One may suppose future transaction management is doable, but the user must consent, creating an impossible loop.
I passed away and must send a transaction to the person I intended to deliver it to.
I have to confirm or authorize the transaction, but I'm dead.
In crypto, scheduling a future transaction wouldn't function. To transfer the wallet and its contents, we'd need the private keys and/or seed phrase. Minimizing private key exposure is crucial to protecting your crypto from hackers, social engineering, and phishing. People have lost private keys after utilizing Life Hack-type tactics to secure them. People that break and hide their keys, lose them, or make them unreadable won't help with managing and/or transferring. This will require a derived solution.

Legal Challenges and Implications
Unlike routine cryptocurrency transfers and transactions, local laws may require special considerations. Even in the traditional world, estate/inheritance taxes, how assets will be split, and who executes the will must be considered. Many lawyers aren't crypto-savvy, which complicates the matter. There will be many hoops to jump through to safeguard your crypto and traditional assets and give them to loved ones.
Knowing RUFADAA/UFADAA, depending on your state, is vital for Americans. UFADAA offers executors and trustees access to online accounts (which crypto wallets would fall into). RUFADAA was changed to limit access to the executor to protect assets. RUFADAA outlines how digital assets are administered following death and incapacity in the US.
A Succession Solution
Having a will and talking about who would get what is the first step to having a solution, but using a Dad Mans Switch is a perfect tool for such unforeseen circumstances. As long as the switch's controller has control, nothing happens. Losing control of the switch initiates a state transition.
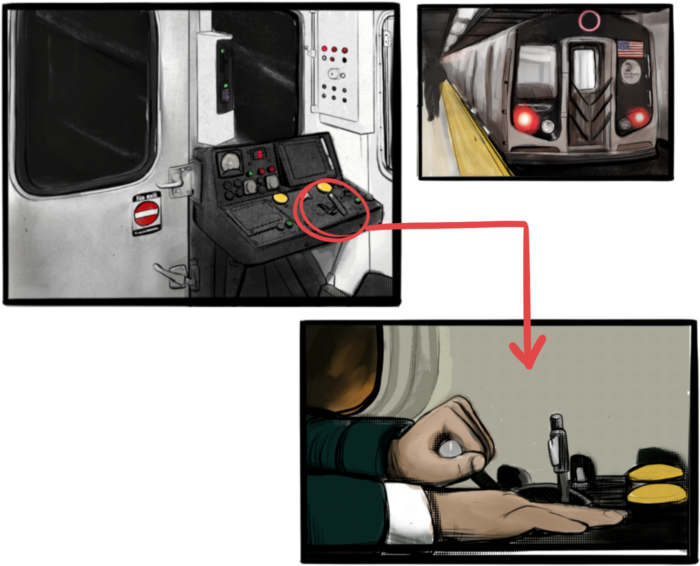
Subway or railway operations are examples. Modern control systems need the conductor to hold a switch to keep the train going. If they can't, the train stops.

Enter Sarcophagus
Sarcophagus is a decentralized dead man's switch built on Ethereum and Arweave. Sarcophagus allows actors to maintain control of their possessions even while physically unable to do so. Using a programmable dead man's switch and dual encryption, anything can be kept and passed on. This covers assets, secrets, seed phrases, and other use cases to provide authority and control back to the user and release trustworthy services from this work. Sarcophagus is built on a decentralized, transparent open source codebase. Sarcophagus is there if you're unprepared.


Vitalik
4 years ago
An approximate introduction to how zk-SNARKs are possible (part 2)
If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? But it turns out that there is a clever solution.
Polynomials
Polynomials are a special class of algebraic expressions of the form:
- x+5
- x^4
- x^3+3x^2+3x+1
- 628x^{271}+318x^{270}+530x^{269}+…+69x+381
i.e. they are a sum of any (finite!) number of terms of the form cx^k
There are many things that are fascinating about polynomials. But here we are going to zoom in on a particular one: polynomials are a single mathematical object that can contain an unbounded amount of information (think of them as a list of integers and this is obvious). The fourth example above contained 816 digits of tau, and one can easily imagine a polynomial that contains far more.
Furthermore, a single equation between polynomials can represent an unbounded number of equations between numbers. For example, consider the equation A(x)+ B(x) = C(x). If this equation is true, then it's also true that:
- A(0)+B(0)=C(0)
- A(1)+B(1)=C(1)
- A(2)+B(2)=C(2)
- A(3)+B(3)=C(3)
And so on for every possible coordinate. You can even construct polynomials to deliberately represent sets of numbers so you can check many equations all at once. For example, suppose that you wanted to check:
- 12+1=13
- 10+8=18
- 15+8=23
- 15+13=28
You can use a procedure called Lagrange interpolation to construct polynomials A(x) that give (12,10,15,15) as outputs at some specific set of coordinates (eg. (0,1,2,3)), B(x) the outputs (1,8,8,13) on thos same coordinates, and so forth. In fact, here are the polynomials:
- A(x)=-2x^3+\frac{19}{2}x^2-\frac{19}{2}x+12
- B(x)=2x^3-\frac{19}{2}x^2+\frac{29}{2}x+1
- C(x)=5x+13
Checking the equation A(x)+B(x)=C(x) with these polynomials checks all four above equations at the same time.
Comparing a polynomial to itself
You can even check relationships between a large number of adjacent evaluations of the same polynomial using a simple polynomial equation. This is slightly more advanced. Suppose that you want to check that, for a given polynomial F, F(x+2)=F(x)+F(x+1) with the integer range {0,1…89} (so if you also check F(0)=F(1)=1, then F(100) would be the 100th Fibonacci number)
As polynomials, F(x+2)-F(x+1)-F(x) would not be exactly zero, as it could give arbitrary answers outside the range x={0,1…98}. But we can do something clever. In general, there is a rule that if a polynomial P is zero across some set S=\{x_1,x_2…x_n\} then it can be expressed as P(x)=Z(x)*H(x), where Z(x)=(x-x_1)*(x-x_2)*…*(x-x_n) and H(x) is also a polynomial. In other words, any polynomial that equals zero across some set is a (polynomial) multiple of the simplest (lowest-degree) polynomial that equals zero across that same set.
Why is this the case? It is a nice corollary of polynomial long division: the factor theorem. We know that, when dividing P(x) by Z(x), we will get a quotient Q(x) and a remainder R(x) is strictly less than that of Z(x). Since we know that P is zero on all of S, it means that R has to be zero on all of S as well. So we can simply compute R(x) via polynomial interpolation, since it's a polynomial of degree at most n-1 and we know n values (the zeros at S). Interpolating a polynomial with all zeroes gives the zero polynomial, thus R(x)=0 and H(x)=Q(x).
Going back to our example, if we have a polynomial F that encodes Fibonacci numbers (so F(x+2)=F(x)+F(x+1) across x=\{0,1…98\}), then I can convince you that F actually satisfies this condition by proving that the polynomial P(x)=F(x+2)-F(x+1)-F(x) is zero over that range, by giving you the quotient:
H(x)=\frac{F(x+2)-F(x+1)-F(x)}{Z(x)}
Where Z(x) = (x-0)*(x-1)*…*(x-98).
You can calculate Z(x) yourself (ideally you would have it precomputed), check the equation, and if the check passes then F(x) satisfies the condition!
Now, step back and notice what we did here. We converted a 100-step-long computation into a single equation with polynomials. Of course, proving the N'th Fibonacci number is not an especially useful task, especially since Fibonacci numbers have a closed form. But you can use exactly the same basic technique, just with some extra polynomials and some more complicated equations, to encode arbitrary computations with an arbitrarily large number of steps.
see part 3

Jonathan Vanian
4 years ago
What is Terra? Your guide to the hot cryptocurrency
With cryptocurrencies like Bitcoin, Ether, and Dogecoin gyrating in value over the past few months, many people are looking at so-called stablecoins like Terra to invest in because of their more predictable prices.
Terraform Labs, which oversees the Terra cryptocurrency project, has benefited from its rising popularity. The company said recently that investors like Arrington Capital, Lightspeed Venture Partners, and Pantera Capital have pledged $150 million to help it incubate various crypto projects that are connected to Terra.
Terraform Labs and its partners have built apps that operate on the company’s blockchain technology that helps keep a permanent and shared record of the firm’s crypto-related financial transactions.
Here’s what you need to know about Terra and the company behind it.
What is Terra?
Terra is a blockchain project developed by Terraform Labs that powers the startup’s cryptocurrencies and financial apps. These cryptocurrencies include the Terra U.S. Dollar, or UST, that is pegged to the U.S. dollar through an algorithm.
Terra is a stablecoin that is intended to reduce the volatility endemic to cryptocurrencies like Bitcoin. Some stablecoins, like Tether, are pegged to more conventional currencies, like the U.S. dollar, through cash and cash equivalents as opposed to an algorithm and associated reserve token.
To mint new UST tokens, a percentage of another digital token and reserve asset, Luna, is “burned.” If the demand for UST rises with more people using the currency, more Luna will be automatically burned and diverted to a community pool. That balancing act is supposed to help stabilize the price, to a degree.
“Luna directly benefits from the economic growth of the Terra economy, and it suffers from contractions of the Terra coin,” Terraform Labs CEO Do Kwon said.
Each time someone buys something—like an ice cream—using UST, that transaction generates a fee, similar to a credit card transaction. That fee is then distributed to people who own Luna tokens, similar to a stock dividend.
Who leads Terra?
The South Korean firm Terraform Labs was founded in 2018 by Daniel Shin and Kwon, who is now the company’s CEO. Kwon is a 29-year-old former Microsoft employee; Shin now heads the Chai online payment service, a Terra partner. Kwon said many Koreans have used the Chai service to buy goods like movie tickets using Terra cryptocurrency.
Terraform Labs does not make money from transactions using its crypto and instead relies on outside funding to operate, Kwon said. It has raised $57 million in funding from investors like HashKey Digital Asset Group, Divergence Digital Currency Fund, and Huobi Capital, according to deal-tracking service PitchBook. The amount raised is in addition to the latest $150 million funding commitment announced on July 16.
What are Terra’s plans?
Terraform Labs plans to use Terra’s blockchain and its associated cryptocurrencies—including one pegged to the Korean won—to create a digital financial system independent of major banks and fintech-app makers. So far, its main source of growth has been in Korea, where people have bought goods at stores, like coffee, using the Chai payment app that’s built on Terra’s blockchain. Kwon said the company’s associated Mirror trading app is experiencing growth in China and Thailand.
Meanwhile, Kwon said Terraform Labs would use its latest $150 million in funding to invest in groups that build financial apps on Terra’s blockchain. He likened the scouting and investing in other groups as akin to a “Y Combinator demo day type of situation,” a reference to the popular startup pitch event organized by early-stage investor Y Combinator.
The combination of all these Terra-specific financial apps shows that Terraform Labs is “almost creating a kind of bank,” said Ryan Watkins, a senior research analyst at cryptocurrency consultancy Messari.
In addition to cryptocurrencies, Terraform Labs has a number of other projects including the Anchor app, a high-yield savings account for holders of the group’s digital coins. Meanwhile, people can use the firm’s associated Mirror app to create synthetic financial assets that mimic more conventional ones, like “tokenized” representations of corporate stocks. These synthetic assets are supposed to be helpful to people like “a small retail trader in Thailand” who can more easily buy shares and “get some exposure to the upside” of stocks that they otherwise wouldn’t have been able to obtain, Kwon said. But some critics have said the U.S. Securities and Exchange Commission may eventually crack down on synthetic stocks, which are currently unregulated.
What do critics say?
Terra still has a long way to go to catch up to bigger cryptocurrency projects like Ethereum.
Most financial transactions involving Terra-related cryptocurrencies have originated in Korea, where its founders are based. Although Terra is becoming more popular in Korea thanks to rising interest in its partner Chai, it’s too early to say whether Terra-related currencies will gain traction in other countries.
Terra’s blockchain runs on a “limited number of nodes,” said Messari’s Watkins, referring to the computers that help keep the system running. That helps reduce latency that may otherwise slow processing of financial transactions, he said.
But the tradeoff is that Terra is less “decentralized” than other blockchain platforms like Ethereum, which is powered by thousands of interconnected computing nodes worldwide. That could make Terra less appealing to some blockchain purists.
You might also like

Quant Galore
3 years ago
I created BAW-IV Trading because I was short on money.
More retail traders means faster, more sophisticated, and more successful methods.
Tech specifications
Only requires a laptop and an internet connection.
We'll use OpenBB's research platform for data/analysis.
Pricing and execution on Options-Quant

Background
You don't need to know the arithmetic details to use this method.
Black-Scholes is a popular option pricing model. It's best for pricing European options. European options are only exercisable at expiration, unlike American options. American options are always exercisable.
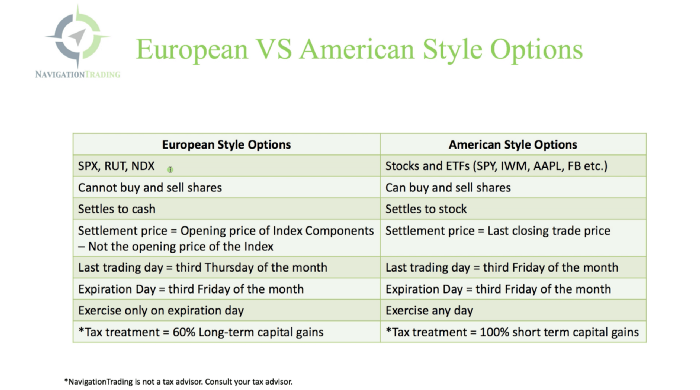
American options carry a premium to cover for the risk of early exercise. The Black-Scholes model doesn't account for this premium, hence it can't price genuine, traded American options.
Barone-Adesi-Whaley (BAW) model. BAW modifies Black-Scholes. It accounts for exercise risk premium and stock dividends. It adds the option's early exercise value to the Black-Scholes value.
The trader need not know the formulaic derivations of this model.
https://ir.nctu.edu.tw/bitstream/11536/14182/1/000264318900005.pdf
Strategy
This strategy targets implied volatility. First, we'll locate liquid options that expire within 30 days and have minimal implied volatility.
After selecting the option that meets the requirements, we price it to get the BAW implied volatility (we choose BAW because it's a more accurate Black-Scholes model). If estimated implied volatility is larger than market volatility, we'll capture the spread.
(Calculated IV — Market IV) = (Profit)
Some approaches to target implied volatility are pricey and inaccessible to individual investors. The best and most cost-effective alternative is to acquire a straddle and delta hedge. This may sound terrifying and pricey, but as shown below, it's much less so.
The Trade
First, we want to find our ideal option, so we use OpenBB terminal to screen for options that:
Have an IV at least 5% lower than the 20-day historical IV
Are no more than 5% out-of-the-money
Expire in less than 30 days
We query:
stocks/options/screen/set low_IV/scr --export Output.csv
This uses the screener function to screen for options that satisfy the above criteria, which we specify in the low IV preset (more on custom presets here). It then saves the matching results to a csv(Excel) file for viewing and analysis.
Stick to liquid names like SPY, AAPL, and QQQ since getting out of a position is just as crucial as getting in. Smaller, illiquid names have higher inefficiencies, which could restrict total profits.

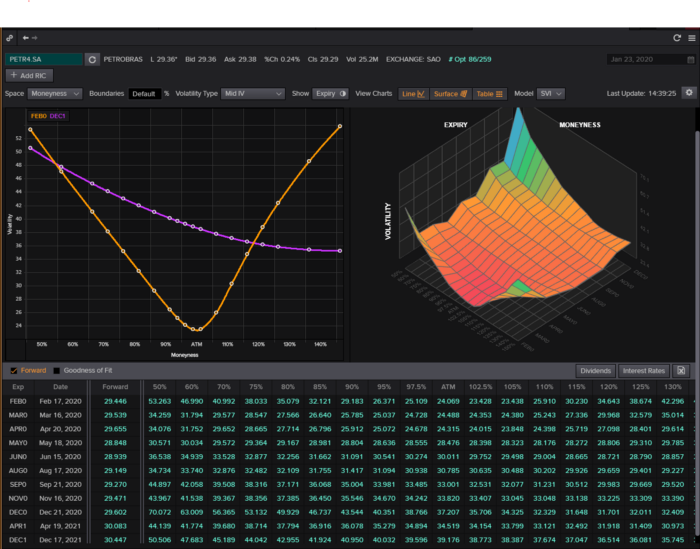
We calculate IV using the BAWbisection model (the bisection is a method of calculating IV, more can be found here.) We price the IV first.

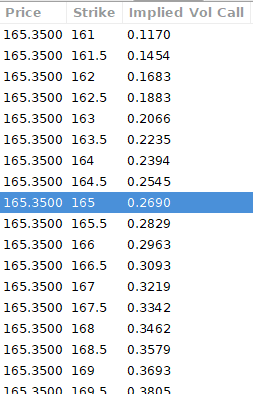
According to the BAW model, implied volatility at this level should be priced at 26.90%. When re-pricing the put, IV is 24.34%, up 3%.
Now it's evident. We must purchase the straddle (long the call and long the put) assuming the computed implied volatility is more appropriate and efficient than the market's. We just want to speculate on volatility, not price fluctuations, thus we delta hedge.
The Fun Starts
We buy both options for $7.65. (x100 multiplier). Initial delta is 2. For every dollar the stock price swings up or down, our position value moves $2.

We want delta to be 0 to avoid price vulnerability. A delta of 0 suggests our position's value won't change from underlying price changes. Being delta-hedged allows us to profit/lose from implied volatility. Shorting 2 shares makes us delta-neutral.

That's delta hedging. (Share price * shares traded) = $330.7 to become delta-neutral. You may have noted that delta is not truly 0.00. This is common since delta-hedging means getting as near to 0 as feasible, since it is rare for deltas to align at 0.00.
Now we're vulnerable to changes in Vega (and Gamma, but given we're dynamically hedging, it's not a big risk), or implied volatility. We wanted to gamble that the position's IV would climb by at least 2%, so we'll maintain it delta-hedged and watch IV.
Because the underlying moves continually, the option's delta moves continuously. A trader can short/long 5 AAPL shares at most. Paper trading lets you practice delta-hedging. Being quick-footed will help with this tactic.
Profit-Closing
As expected, implied volatility rose. By 10 minutes before market closure, the call's implied vol rose to 27% and the put's to 24%. This allowed us to sell the call for $4.95 and the put for $4.35, creating a profit of $165.

You may pull historical data to see how this trade performed. Note the implied volatility and pricing in the final options chain for August 5, 2022 (the position date).

Final Thoughts
Congratulations, that was a doozy. To reiterate, we identified tickers prone to increased implied volatility by screening OpenBB's low IV setting. We double-checked the IV by plugging the price into Options-BAW Quant's model. When volatility was off, we bought a straddle and delta-hedged it. Finally, implied volatility returned to a normal level, and we profited on the spread.
The retail trading space is very quickly catching up to that of institutions. Commissions and fees used to kill this method, but now they cost less than $5. Watching momentum, technical analysis, and now quantitative strategies evolve is intriguing.
I'm not linked with these sites and receive no financial benefit from my writing.
Tell me how your experience goes and how I helped; I love success tales.

Matthew Cluff
3 years ago
GTO Poker 101
"GTO" (Game Theory Optimal) has been used a lot in poker recently. To clarify its meaning and application, the aim of this article is to define what it is, when to use it when playing, what strategies to apply for how to play GTO poker, for beginner and more advanced players!
Poker GTO
In poker, you can choose between two main winning strategies:
Exploitative play maximizes expected value (EV) by countering opponents' sub-optimal plays and weaker tendencies. Yes, playing this way opens you up to being exploited, but the weaker opponents you're targeting won't change their game to counteract this, allowing you to reap maximum profits over the long run.
GTO (Game-Theory Optimal): You try to play perfect poker, which forces your opponents to make mistakes (which is where almost all of your profit will be derived from). It mixes bluffs or semi-bluffs with value bets, clarifies bet sizes, and more.
GTO vs. Exploitative: Which is Better in Poker?
Before diving into GTO poker strategy, it's important to know which of these two play styles is more profitable for beginners and advanced players. The simple answer is probably both, but usually more exploitable.
Most players don't play GTO poker and can be exploited in their gameplay and strategy, allowing for more profits to be made using an exploitative approach. In fact, it’s only in some of the largest games at the highest stakes that GTO concepts are fully utilized and seen in practice, and even then, exploitative plays are still sometimes used.
Knowing, understanding, and applying GTO poker basics will create a solid foundation for your poker game. It's also important to understand GTO so you can deviate from it to maximize profits.
GTO Poker Strategy
According to Ed Miller's book "Poker's 1%," the most fundamental concept that only elite poker players understand is frequency, which could be in relation to cbets, bluffs, folds, calls, raises, etc.
GTO poker solvers (downloadable online software) give solutions for how to play optimally in any given spot and often recommend using mixed strategies based on select frequencies.
In a river situation, a solver may tell you to call 70% of the time and fold 30%. It may also suggest calling 50% of the time, folding 35% of the time, and raising 15% of the time (with a certain range of hands).
Frequencies are a fundamental and often unrecognized part of poker, but they run through these 5 GTO concepts.
1. Preflop ranges
To compensate for positional disadvantage, out-of-position players must open tighter hand ranges.
Premium starting hands aren't enough, though. Considering GTO poker ranges and principles, you want a good, balanced starting hand range from each position with at least some hands that can make a strong poker hand regardless of the flop texture (low, mid, high, disconnected, etc).
Below is a GTO preflop beginner poker chart for online 6-max play, showing which hand ranges one should open-raise with. Table positions are color-coded (see key below).
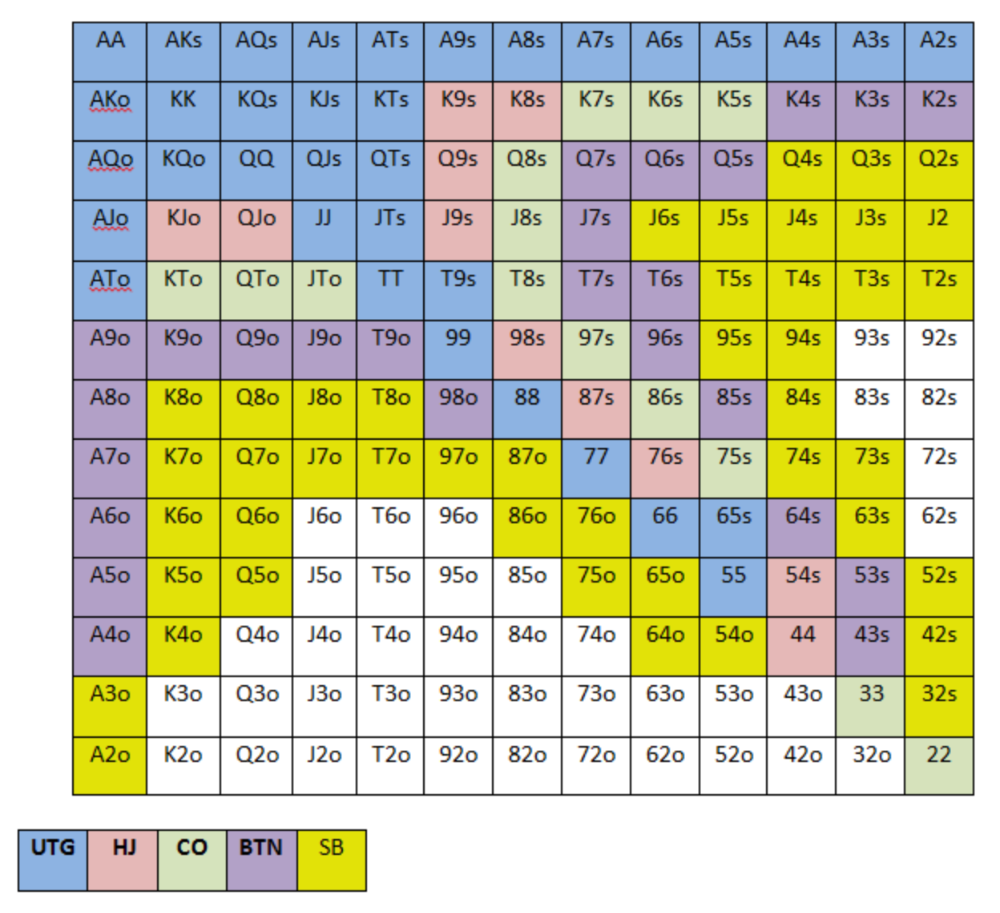
NOTE: For GTO play, it's advisable to use a mixed strategy for opening in the small blind, combining open-limps and open-raises for various hands. This cannot be illustrated with the color system used for the chart.
Choosing which hands to play is often a math problem, as discussed below.
Other preflop GTO poker charts include which hands to play after a raise, which to 3bet, etc. Solvers can help you decide which preflop hands to play (call, raise, re-raise, etc.).
2. Pot Odds
Always make +EV decisions that profit you as a poker player. Understanding pot odds (and equity) can help.
Postflop Pot Odds
Let’s say that we have JhTh on a board of 9h8h2s4c (open-ended straight-flush draw). We have $40 left and $50 in the pot. He has you covered and goes all-in. As calling or folding are our only options, playing GTO involves calculating whether a call is +EV or –EV. (The hand was empty.)
Any remaining heart, Queen, or 7 wins the hand. This means we can improve 15 of 46 unknown cards, or 32.6% of the time.
What if our opponent has a set? The 4h or 2h could give us a flush, but it could also give the villain a boat. If we reduce outs from 15 to 14.5, our equity would be 31.5%.
We must now calculate pot odds.
(bet/(our bet+pot)) = pot odds
= $50 / ($40 + $90)
= $40 / $130
= 30.7%
To make a profitable call, we need at least 30.7% equity. This is a profitable call as we have 31.5% equity (even if villain has a set). Yes, we will lose most of the time, but we will make a small profit in the long run, making a call correct.
Pot odds aren't just for draws, either. If an opponent bets 50% pot, you get 3 to 1 odds on a call, so you must win 25% of the time to be profitable. If your current hand has more than 25% equity against your opponent's perceived range, call.
Preflop Pot Odds
Preflop, you raise to 3bb and the button 3bets to 9bb. You must decide how to act. In situations like these, we can actually use pot odds to assist our decision-making.
This pot is:
(our open+3bet size+small blind+big blind)
(3bb+9bb+0.5bb+1bb)
= 13.5
This means we must call 6bb to win a pot of 13.5bb, which requires 30.7% equity against the 3bettor's range.
Three additional factors must be considered:
Being out of position on our opponent makes it harder to realize our hand's equity, as he can use his position to put us in tough spots. To profitably continue against villain's hand range, we should add 7% to our equity.
Implied Odds / Reverse Implied Odds: The ability to win or lose significantly more post-flop (than pre-flop) based on our remaining stack.
While statistics on 3bet stats can be gained with a large enough sample size (i.e. 8% 3bet stat from button), the numbers don't tell us which 8% of hands villain could be 3betting with. Both polarized and depolarized charts below show 8% of possible hands.
7.4% of hands are depolarized.
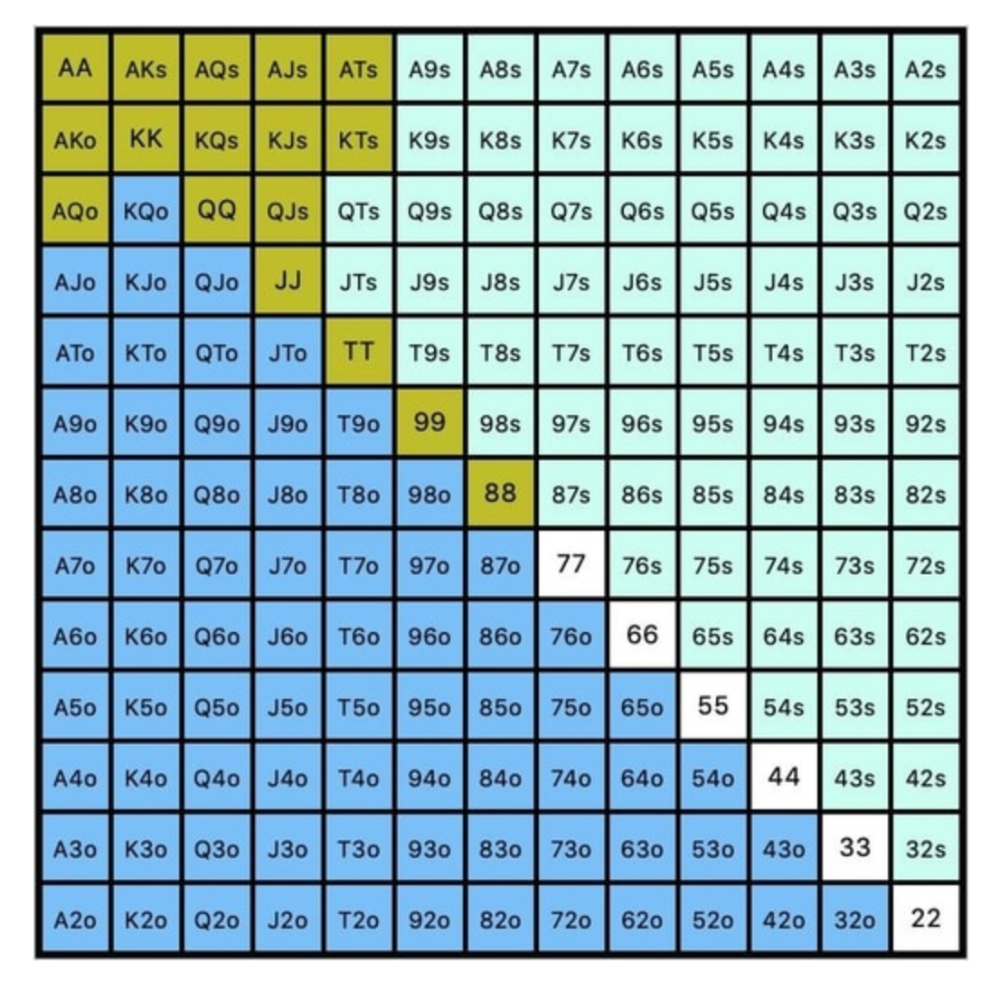
Polarized Hand range (7.54%):
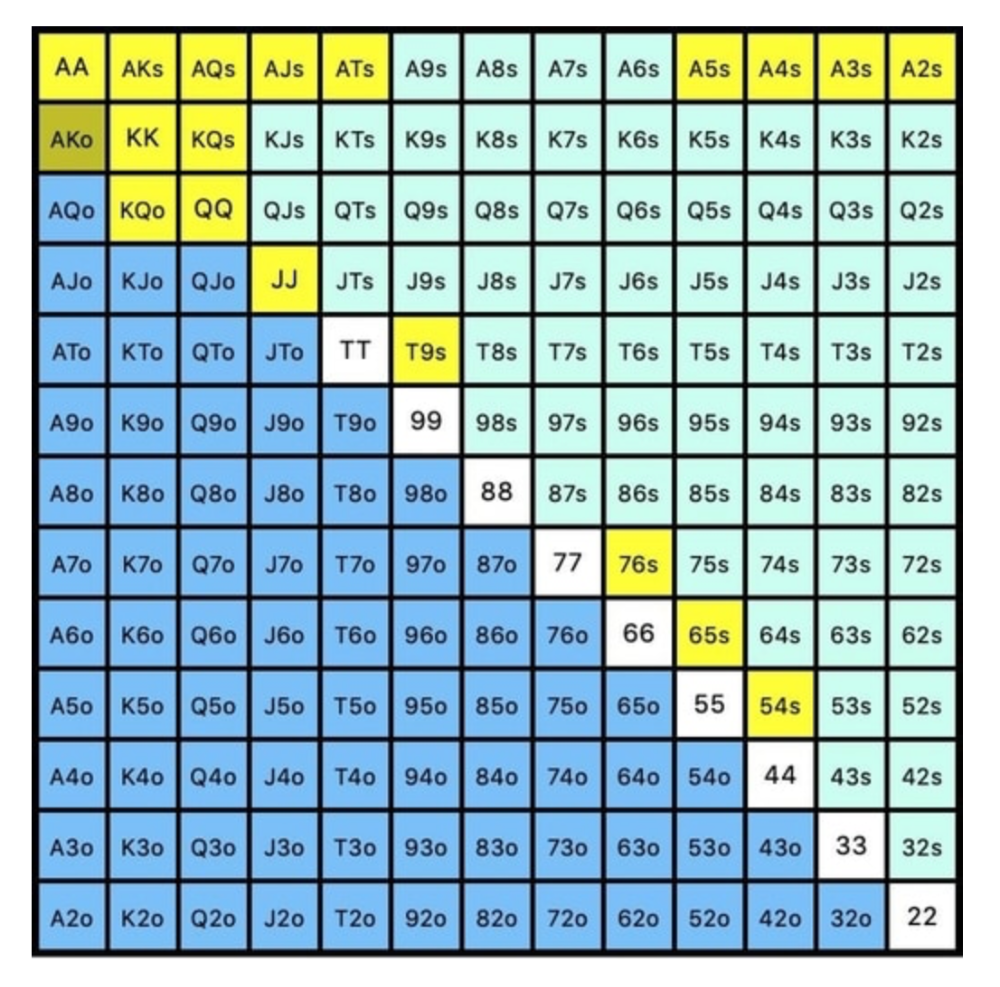
Each hand range has different contents. We don't know if he 3bets some hands and calls or folds others.
Using an exploitable strategy can help you play a hand range correctly. The next GTO concept will make things easier.
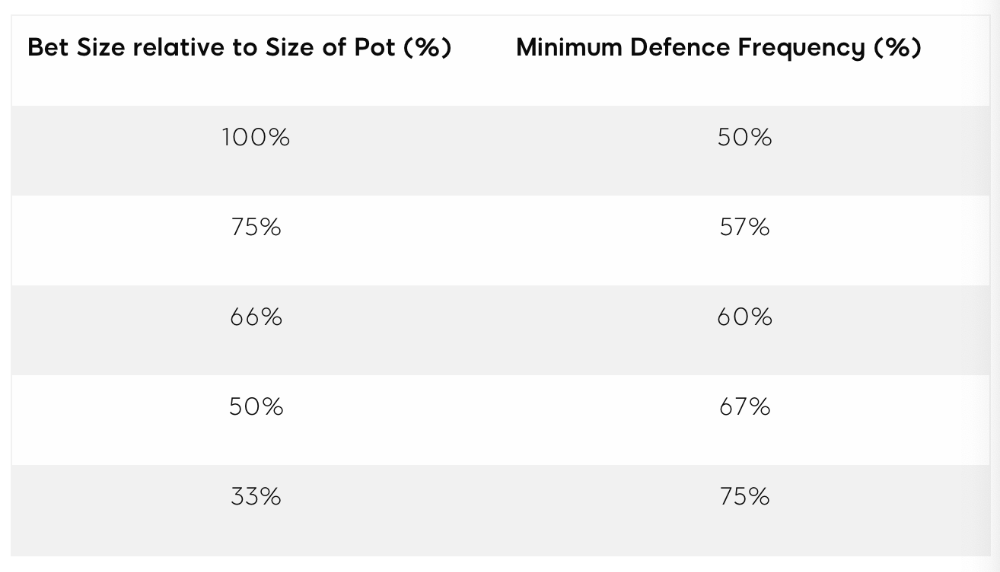
3. Minimum Defense Frequency:
This concept refers to the % of our range we must continue with (by calling or raising) to avoid being exploited by our opponents. This concept is most often used off-table and is difficult to apply in-game.
These beginner GTO concepts will help your decision-making during a hand, especially against aggressive opponents.
MDF formula:
MDF = POT SIZE/(POT SIZE+BET SIZE)
Here's a poker GTO chart of common bet sizes and minimum defense frequency.
Take the number of hand combos in your starting hand range and use the MDF to determine which hands to continue with. Choose hands with the most playability and equity against your opponent's betting range.
Say you open-raise HJ and BB calls. Qh9h6c flop. Your opponent leads you for a half-pot bet. MDF suggests keeping 67% of our range.
Using the above starting hand chart, we can determine that the HJ opens 254 combos:
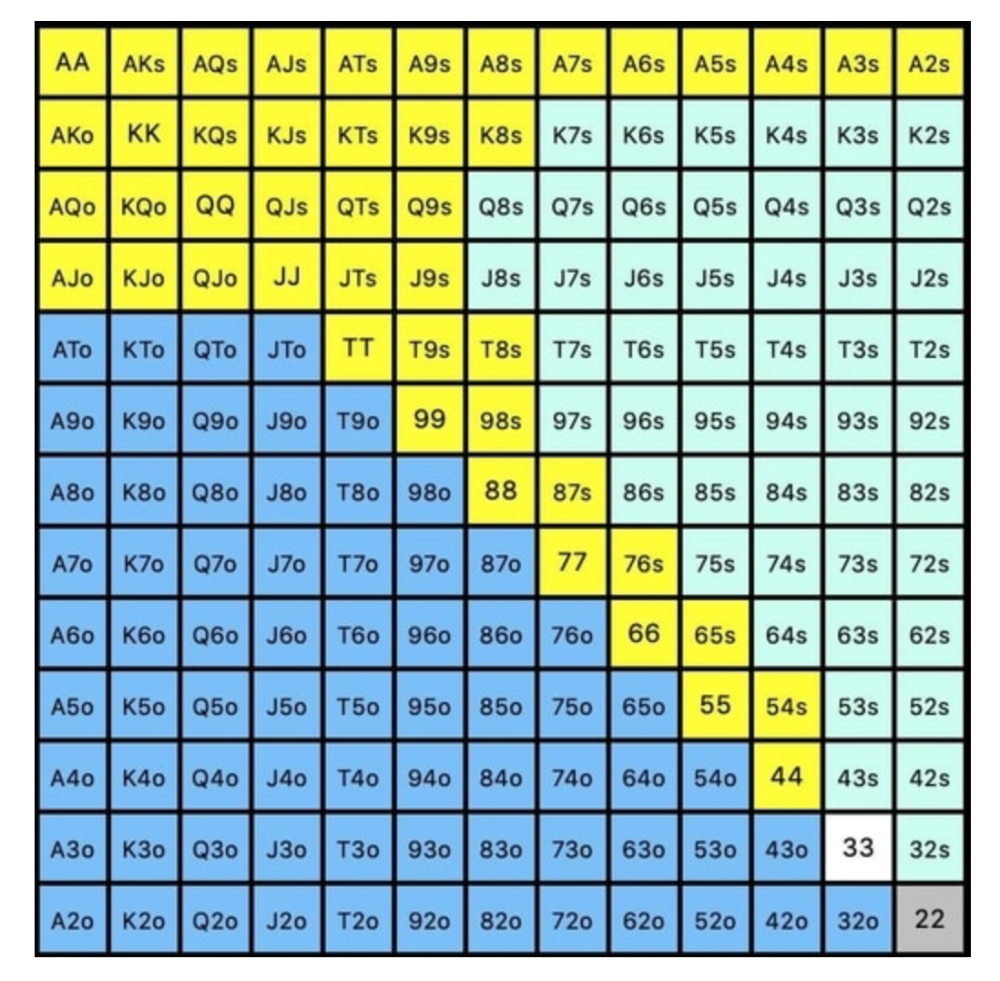
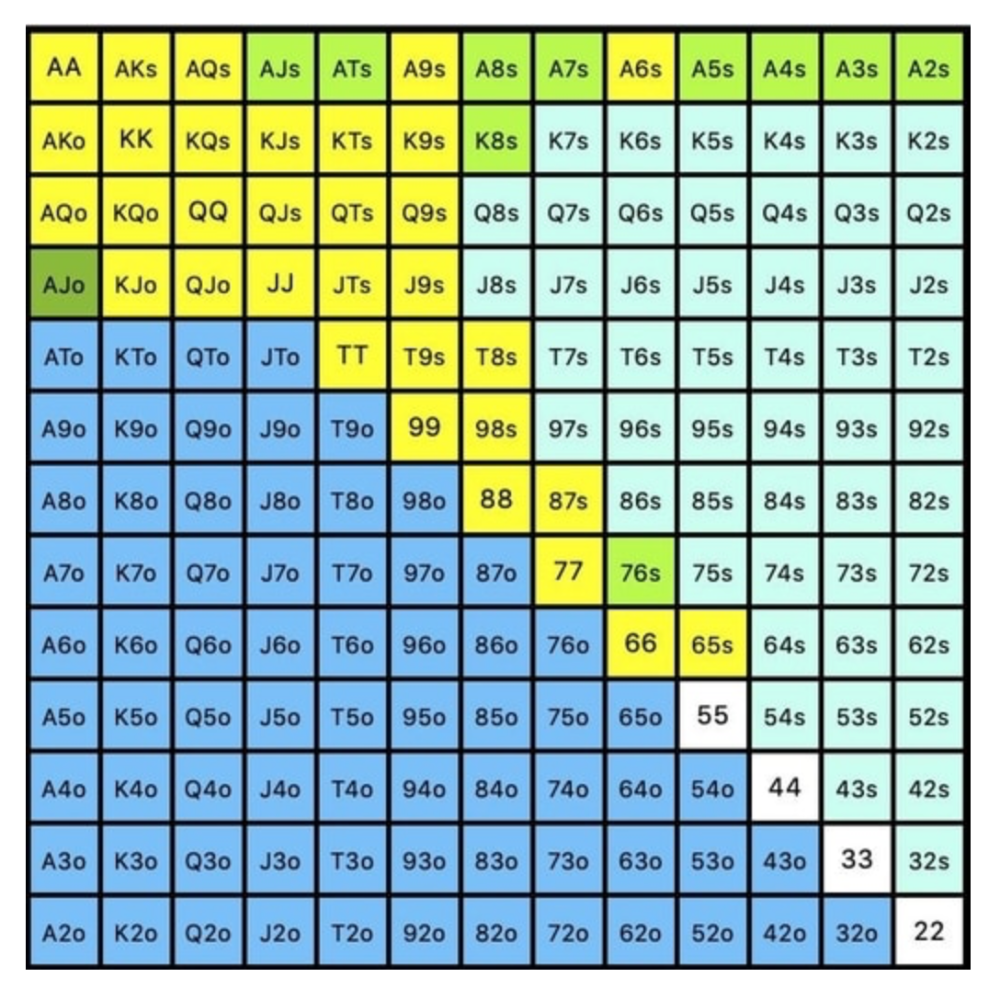
We must defend 67% of these hands, or 170 combos, according to MDF. Hands we should keep include:
Flush draws
Open-Ended Straight Draws
Gut-Shot Straight Draws
Overcards
Any Pair or better
So, our flop continuing range could be:
Some highlights:
Fours and fives have little chance of improving on the turn or river.
We only continue with AX hearts (with a flush draw) without a pair or better.
We'll also include 4 AJo combos, all of which have the Ace of hearts, and AcJh, which can block a backdoor nut flush combo.
Let's assume all these hands are called and the turn is blank (2 of spades). Opponent bets full-pot. MDF says we must defend 50% of our flop continuing range, or 85 of 170 combos, to be unexploitable. This strategy includes our best flush draws, straight draws, and made hands.
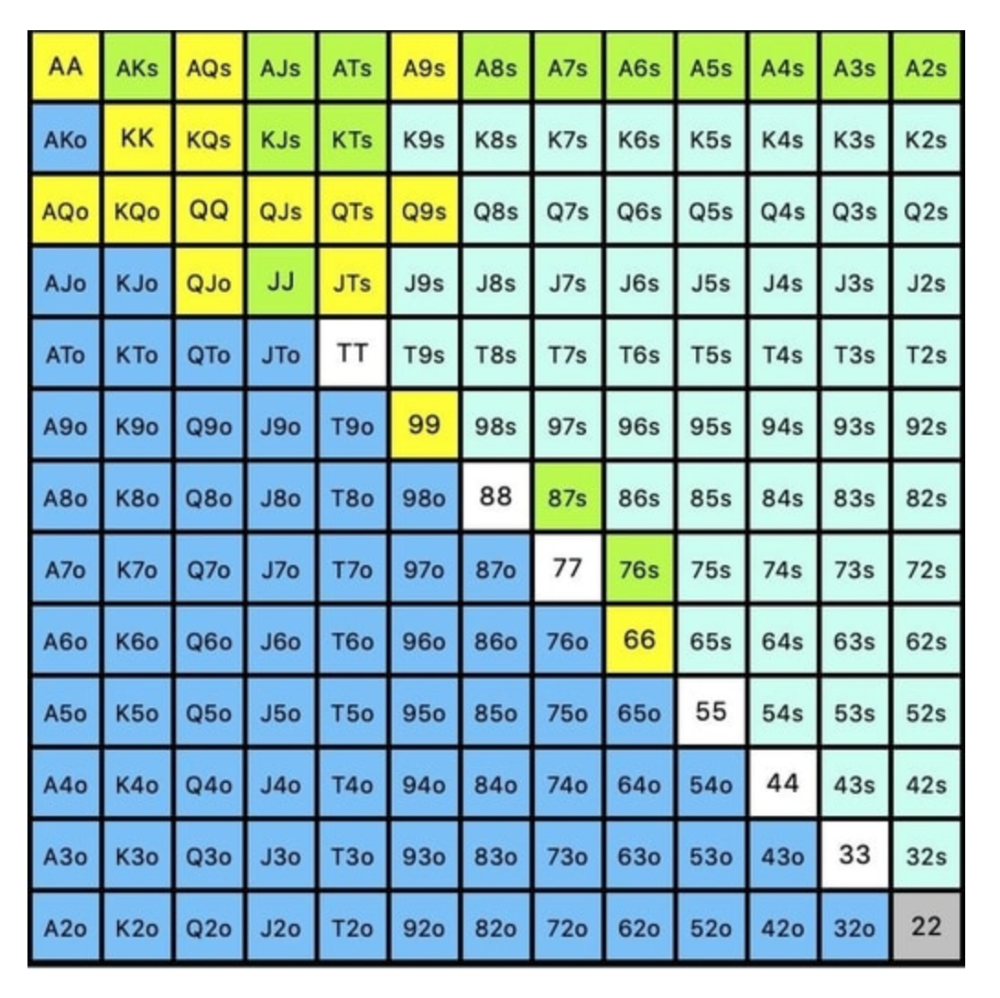
Here, we keep combining:
Nut flush draws
Pair + flush draws
GS + flush draws
Second Pair, Top Kicker+
One combo of JJ that doesn’t block the flush draw or backdoor flush draw.
On the river, we can fold our missed draws and keep our best made hands. When calling with weaker hands, consider blocker effects and card removal to avoid overcalling and decide which combos to continue.
4. Poker GTO Bet Sizing
To avoid being exploited, balance your bluffs and value bets. Your betting range depends on how much you bet (in relation to the pot). This concept only applies on the river, as draws (bluffs) on the flop and turn still have equity (and are therefore total bluffs).
On the flop, you want a 2:1 bluff-to-value-bet ratio. On the flop, there won't be as many made hands as on the river, and your bluffs will usually contain equity. The turn should have a "bluffing" ratio of 1:1. Use the chart below to determine GTO river bluff frequencies (relative to your bet size):
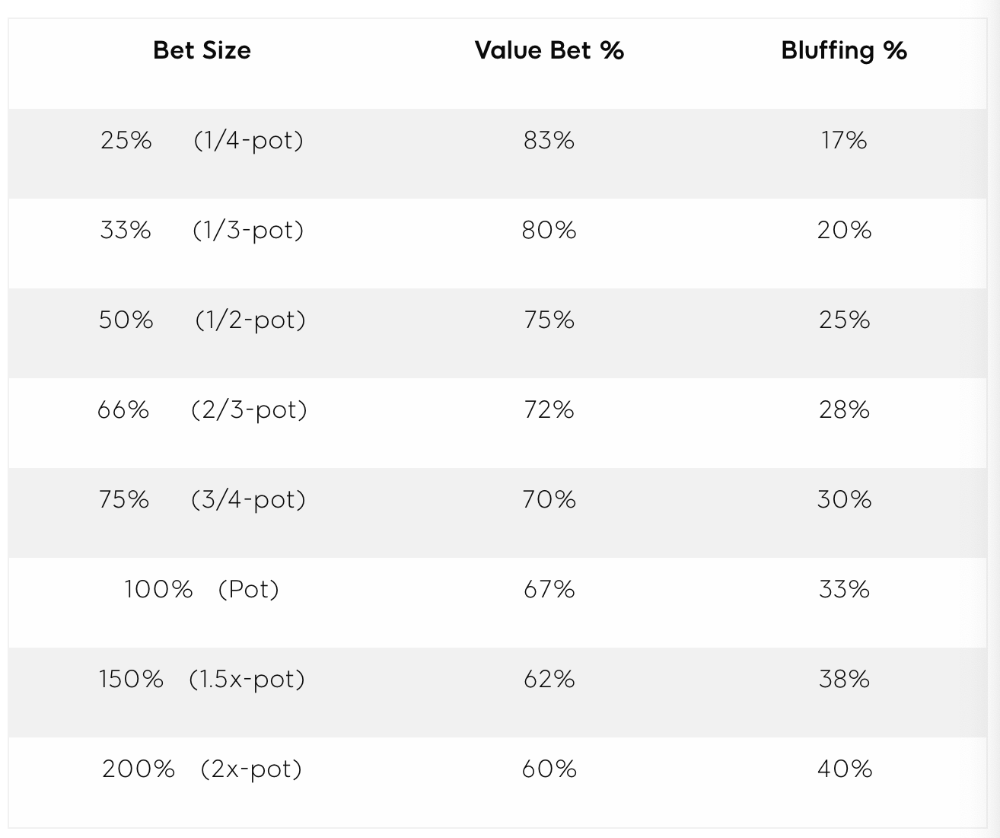
This chart relates to your opponent's pot odds. If you bet 50% pot, your opponent gets 3:1 odds and must win 25% of the time to call. Poker GTO theory suggests including 25% bluff combinations in your betting range so you're indifferent to your opponent calling or folding.
Best river bluffs don't block hands you want your opponent to have (or not have). For example, betting with missed Ace-high flush draws is often a mistake because you block a missed flush draw you want your opponent to have when bluffing on the river (meaning that it would subsequently be less likely he would have it, if you held two of the flush draw cards). Ace-high usually has some river showdown value.
If you had a 3-flush on the river and wanted to raise, you could bluff raise with AX combos holding the bluff suit Ace. Blocking the nut flush prevents your opponent from using that combo.
5. Bet Sizes and Frequency
GTO beginner strategies aren't just bluffs and value bets. They show how often and how much to bet in certain spots. Top players have benefited greatly from poker solvers, which we'll discuss next.
GTO Poker Software
In recent years, various poker GTO solvers have been released to help beginner, intermediate, and advanced players play balanced/GTO poker in various situations.
PokerSnowie and PioSolver are popular GTO and poker study programs.
While you can't compute players' hand ranges and what hands to bet or check with in real time, studying GTO play strategies with these programs will pay off. It will improve your poker thinking and understanding.
Solvers can help you balance ranges, choose optimal bet sizes, and master cbet frequencies.
GTO Poker Tournament
Late-stage tournaments have shorter stacks than cash games. In order to follow GTO poker guidelines, Nash charts have been created, tweaked, and used for many years (and also when to call, depending on what number of big blinds you have when you find yourself shortstacked).
The charts are for heads-up push/fold. In a multi-player game, the "pusher" chart can only be used if play is folded to you in the small blind. The "caller" chart can only be used if you're in the big blind and assumes a small blind "pusher" (with a much wider range than if a player in another position was open-shoving).
Divide the pusher chart's numbers by 2 to see which hand to use from the Button. Divide the original chart numbers by 4 to find the CO's pushing range. Some of the figures will be impossible to calculate accurately for the CO or positions to the right of the blinds because the chart's highest figure is "20+" big blinds, which is also used for a wide range of hands in the push chart.
Both of the GTO charts below are ideal for heads-up play, but exploitable HU shortstack strategies can lead to more +EV decisions against certain opponents. Following the charts will make your play GTO and unexploitable.
Poker pro Max Silver created the GTO push/fold software SnapShove. (It's accessible online at www.snapshove.com or as iOS or Android apps.)
Players can access GTO shove range examples in the full version. (You can customize the number of big blinds you have, your position, the size of the ante, and many other options.)
In Conclusion
Due to the constantly changing poker landscape, players are always improving their skills. Exploitable strategies often yield higher profit margins than GTO-based approaches, but knowing GTO beginner and advanced concepts can give you an edge for a few reasons.
It creates a solid gameplay base.
Having a baseline makes it easier to exploit certain villains.
You can avoid leveling wars with your opponents by making sound poker decisions based on GTO strategy.
It doesn't require assuming opponents' play styles.
Not results-oriented.
This is just the beginning of GTO and poker theory. Consider investing in the GTO poker solver software listed above to improve your game.

Kaitlin Fritz
3 years ago
The Entrepreneurial Chicken and Egg
University entrepreneurship is like a Willy Wonka Factory of ideas. Classes, roommates, discussions, and the cafeteria all inspire new ideas. I've seen people establish a business without knowing its roots.
Chicken or egg? On my mind: I've asked university founders around the world whether the problem or solution came first.
The Problem
One African team I met started with the “instant noodles” problem in their academic ecosystem. Many of us have had money issues in college, which may have led to poor nutritional choices.
Many university students in a war-torn country ate quick noodles or pasta for dinner.

Noodles required heat, water, and preparation in the boarding house. Unreliable power from one hot plate per blue moon. What's healthier, easier, and tastier than sodium-filled instant pots?
BOOM. They were fixing that. East African kids need affordable, nutritious food.
This is a real difficulty the founders faced every day with hundreds of comrades.
This sparked their serendipitous entrepreneurial journey and became their business's cornerstone.
The Solution
I asked a UK team about their company idea. They said the solution fascinated them.
The crew was fiddling with social media algorithms. Why are some people more popular? They were studying platforms and social networks, which offered a way for them.

Solving a problem? Yes. Long nights of university research lead them to it. Is this like world hunger? Social media influencers confront this difficulty regularly.
It made me ponder something. Is there a correct response?
In my heart, yes, but in my head…maybe?
I believe you should lead with empathy and embrace the problem, not the solution. Big or small, businesses should solve problems. This should be your focus. This is especially true when building a social company with an audience in mind.
Philosophically, invention and innovation are occasionally accidental. Also not penalized. Think about bugs and the creation of Velcro, or the inception of Teflon. They tackle difficulties we overlook. The route to the problem may look different, but there is a path there.
There's no golden ticket to the Chicken-Egg debate, but I'll keep looking this summer.
